ТЕМА № 1. ТЕОРИЯ МНОЖЕСТВ
Практикум содержит программу по математике данной специальности, список литературы с указанием страниц, где изложен теоретический материал, перечень разноуровневых заданий для самостоятельного выполнения с образцами решений нулевого варианта. Пособие предназначено для самостоятельной работы и совершенствования навыков решения задач по курсу математики, а также для выполнения контрольной работы № 1 студентами отделения заочного обучения.
УДК 372.8: 51(07) ББК 74.262.21+74.58 © Издательство БрГУ ISBN © Онискевич Т.С. 2006 ОГЛАВЛЕНИЕ Предисловие …………………………………………………………….5
Разноуровневые задания по теме № 1 «Теория множеств»: Задания 1 уровня ………………………………………………………..7 Образцы решения заданий 1 уровня …………………………………..8 Задания 2 уровня ………………………………………………………..9 Образцы решения заданий 2 уровня …………………………………10 Задания 3 уровня ………………………………………………………12 Образцы решения заданий 3 уровня …………………………………14 Задания 4 уровня ………………………………………………………15 Задания 5 уровня ………………………………………………………17
Разноуровневые задания по теме № 2 «Логика высказываний»: Задания 1 уровня ………………………………………………………18 Образцы решения заданий 1 уровня …………………………………20 Задания 2 уровня ………………………………………………………21 Образцы решения заданий 2 уровня …………………………………22 Задания 3 уровня ………………………………………………………23 Образцы решения заданий 3 уровня …………………………………25 Задания 4 уровня ………………………………………………………26 Задания 5 уровня ………………………………………………………26
Разноуровневые задания по теме № 3 «Логика предикатов»: Задания 1 уровня ………………………………………………………27 Образцы решения заданий 1 уровня …………………………………29 Задания 2 уровня ………………………………………………………30 Образцы решения заданий 2 уровня …………………………………31 Задания 3 уровня ………………………………………………………33 Образцы решения заданий 3 уровня …………………………………34 Задания 4 уровня ………………………………………………………36 Задания 5 уровня ………………………………………………………38
Разноуровневые задания по теме № 4 «Комбинаторика»: Задания 1 уровня ………………………………………………………39 Образцы решения заданий 1 уровня …………………………………41 Задания 2 уровня ………………………………………………………41 Образцы решения заданий 2 уровня …………………………………42 Задания 3 уровня ………………………………………………………43 Образцы решения заданий 3 уровня …………………………………44 Задания 4 уровня ………………………………………………………44 Задания 5 уровня ………………………………………………………45
Разноуровневые задания по теме № 5 «Бинарные отношения»: Задания 1 уровня ………………………………………………………46 Образцы решения заданий 1 уровня …………………………………48 Задания 2 уровня ………………………………………………………49 Образцы решения заданий 2 уровня …………………………………50 Задания 3 уровня ………………………………………………………52 Образцы решения заданий 3 уровня …………………………………54 Задания 4 уровня ………………………………………………………55 Задания 5 уровня ………………………………………………………57
Литература ……………………………………………………………..59 ПРЕДИСЛОВИЕ
Практикум по методике с разноуровневыми заданиями предназначен для будущих учителей начальных классов, социальных педагогов, обучающихся заочно. Пособие является руководством по самостоятельному изучению курса математики, поскольку: − содержит программу по математике для студентов специальности «Начальное образование»; − включает список литературы по каждой теме для повторения теоретического материала; − содержит задачи пяти уровней сложности, распределение которых организовано с учетом их постепенного усложнения и увеличения объема теоретических знаний для выполнения; − предполагает самоконтроль и самооценку студентов посредством использования образцов решений 0 варианта для 1 – 3 уровней сложности; − дает возможность произвольного выбора заданий (А или Б) для выполнения в каждом варианте по каждой теме. Часть 1 содержит задания по следующим темам: 1. Теория множеств 2. Логика высказываний 3. Логика предикатов 4. Комбинаторика 5. Бинарные отношения. Студентам предлагаются задания пяти уровней: Первый – уровень узнавания. В эту группу включены задания тестового характера, для выполнения которых необходимы лишь формальные знания основных определений, теорем, свойств. Это, как правило, выбор правильного ответа из нескольких предложенных (закрытые тестовые задания). Второй – уровень неосознанного воспроизведения учебного материала. Задания, соответствующие этому уровню усвоения – несложные задачи на применение усвоенных математических фактов. Наряду с закрытыми, в этой группе предлагаются и открытые тестовые задания. Третий уровень – воспроизведение с осознанным пониманием. Группа заданий, соответствующих этому уровню, включает в себя задачи, аналогичные разобранным в нулевом варианте. Решение задач на этом уровне идет по аналогии. Четвертый уровень – применение знаний в знакомой ситуации. К этой группе относятся более сложные по сравнению с третьим уровнем задачи, но требующие, тем не менее, стандартного подхода к их решению. Пятый – уровень творческого применения знаний. Сюда вошли, в основном, задачи на доказательство математических фактов, формул, нестандартные задачи, требующие применения творческой активности в процессе их решения. Работа состоит из 5 вариантов. Студент выполняет один из вариантов, номер которого определяет преподаватель. Для получения отметки «зачтено» по контрольной работе студент должен осуществить выбор и выполнить: - либо задания первых трех уровней, - либо задания 4 уровня, - либо задания 5 уровня. Студент, выбравший выполнение заданий первых трех уровней, имеет возможность выполнить в каждом из трех уровней задание А или Б по желанию. Например, набор заданий для 1 варианта может быть следующим: «Теория множеств» – задания 1А, 1Б, 1Б; «Логика высказываний» – задания 1Б, 1А, 1Б и т.д. Итого: 5 тем по 3 задания, всего 15 заданий. Студент, выполняющий задания 4 или 5 уровня, выполняет все задания (А и Б), помещенные в его варианте по каждой теме. Контрольная работа 4 уровня (все варианты) состоит из 9 заданий, 5 уровня – из 8 заданий. Распределение вариантов контрольной работы указывает преподаватель. Один из возможных способов распределения такой: 1 вариант – пишут студенты, номера зачетной книжки которых заканчиваются цифрами 0 или 1; 2 вариант – последняя цифра зачетки 2 или 3; 3 вариант – последняя цифра зачетки 4 или 5; 4 вариант – последняя цифра зачетки 6 или 7; 5 вариант – последняя цифра зачетки 8 или 9. Практикум может быть использован студентами дневного отделения для самостоятельной работы по отдельным темам, а также для самооценки уровня знаний по математике и своего продвижения в изучении материала. Автор ТЕМА № 1. ТЕОРИЯ МНОЖЕСТВ Понятие множества. Способы задания множеств. Отношения между множествами: пересечения, включения, равенства. Круги Эйлера. Подмножество. Операции над множествами: объединение, пересечение, разность. Дополнение множества. Декартово произведение множеств. Литература: [1] с. 25-38; [2] с. 5-20, с. 79-82; [3] с. 15-32; [4] с. 12-23; [5] с. 5-25; [6] с. 60-72; [7] с. 6-16.
ТЕОРИЯ МНОЖЕСТВ (задания 1 уровня)
1А. Назовите пары равных множеств: а) А={2, 4, 6} и В={6, 4, 2}; б) А={1, 2, 3} и В={Ι, Ι Ι, Ι Ι Ι }; в) А={{1, 2}, {2, 3}} и В={2, 3, 1}; г) А={
1Б. Каким способом задано множество А в каждом из случаев: а) А={х|хÎ N, х≤ 9}; б) А={1, 2, 3, 4, 5, 6, 7, 8, 9}; в) А={х|хÎ N, 2х+1< 21}.
2А. Для каких пар множеств имеет место отношение включения: а) А={а, в, с, d}, В= {а, с, d}; б) А=Æ, В={Æ }; в) А=Æ, В={а, в, с}; г) А={а, в}, В={а, с, d}.
2Б. А – множество четырехугольников. Принадлежит ли множеству А: 1) параллелограмм, 2) ромб, 3) трапеция, 4) параллелепипед, 5) пирамида?
3А. Даны множества: А={1, 2, 3, 4, 5, 6} и В={х|хÎ Nо, х≤ 15}. Пусть С=АÇ В. Укажите правильный ответ: а) C={х|хÎ N, 6< < х≤ 15}; б) С=[1, 6]; в) С={0, 1, 2, 3, 4, 5, 6}; г) С={х|хÎ N, 1≤ х≤ 6}; д) С={х|хÎ Nо, х≤ 6}.
3Б. Каким способом задано множество В в каждом из случаев: а) В={х|хÎ R, |х|< 2}; б) В=(-2, 2); в) В={х|хÎ R, -2< х< 2};
4А. Даны множества А={2, 4, 6, 8, 10, 12}, В={х|х Î N, х≤ 10}. Пусть С=АÈ В. Укажите правильный ответ: а) С={х|х Î N, х≤ 12}; б) С=В; в) С=А; г) С={х|х Î N, х≤ 10}; д) С={1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12}.
4Б. М – множество всех геометрических фигур плоскости. Принадлежит ли множеству М: а) точка; б) отрезок; в) луч; г) прямая; д) тупой угол.
5А. Даны множества Х={1, 2, 3, 4}, У={а, в, с}. Пусть Z=Х´ У. Укажите правильный ответ: а) Z={(1, а), (2, а), (3, а), (4, а), (1, в), (2, в), (3, в), (4, в), (3, с), (2, с), (1, с)}; б) Z={(1, а), (1, в), (1, с), (2, а), (2, в), (2, с), (3, а), (3, в), (3, с), (4, а), (4, в), (4, с)}; в) Z={(а, 1), (в, 1), (с, 1), (а, 2), (в, 2), (с, 2), (а, 3), (в, 3), (с, 3), (а, 4), (в, 4), (с, 4)}; г) Z={(1, а), (2, в), (3, с), (4, а), (4, в), (4, с)}.
5Б. В – множество натуральных чисел, меньших 14. Какие из записей верны: а) 10Î В, б) 1Î В, в) 0Î В, г) 2/3Î В, д) -10Î В, е) 22Î В?
0А. Для каких пар множеств имеет место отношение включения: а) А=Æ, В=Æ; б) А={а, в, к}, В={к, е, с}; в) А={{а}, а, Æ }, В={а}; г) А={{а, в}, {с, d}, с, d}, В={{а, в}, с}. Решение: а) А=Æ, В=Æ; эти множества находятся в отношении включения, т.к. А=В=Æ, а любое множество является своим же подмножеством, т.е. Æ Ì Æ, значит, АÌ В, ВÌ А. б) А={а, в, к}, В={к, е, с}; эти множества не находятся в отношении включения. Они находятся в отношении пересечения, поскольку имеют один общий элемент к. в) А={{а}, а, Æ }, В={а}; ВÌ А, т.к. множество В входит в множество А как один из его элементов. г) А={{а, в}, {с, d}, с, d}, В={{а, в}, с}; ВÌ А, т.к. каждый элемент множества В является элементом множества А. Обратное утверждение неверно.
0Б. А – множество многоугольников. Принадлежит ли множеству А: а) отрезок; б) треугольник; в) луч; г) призма; д) квадрат? Решение: а) отрезок не принадлежит множеству А, т.к. отрезок - это часть прямой, ограниченная точками с обеих сторон, а не многоугольник; б) треугольник принадлежит множеству А, т.к. треугольником называют многоугольник, имеющий три стороны; в) луч не принадлежит множеству многоугольников, т.к. луч – это полупрямая; г) призма не принадлежит множеству многоугольников, поскольку призма – это многогранник; д) квадрат принадлежит множеству многоугольников, т.к. квадрат – это четырехугольник, являющийся частным случаем многоугольника.
ТЕОРИЯ МНОЖЕСТВ (задания ІІ уровня)
1А. Запишите словами и перечислите элементы каждого из множеств: а) А={х|хÎ N, х< 6}; б) В={ х|хÎ Nо, |х|≤ 5}; в) С={ х|хÎ Z, -1≤ х≤ 6}; г) Д={х|хÎ R, х(х+3)=0}.
1Б. Даны множества: А={3, 4, 5, 6, 7}, В={5, 6, 7, 8, 9, 10}, а) АÈ ВÈ С; б) АÇ ВÇ С; в) АÇ ВÈ С; г) (АÈ С)Ç (ВÈ С).
2А. Прочтите записи и перечислите элементы каждого из множеств: а) М={х|хÎ Nо, х≤ 3}; б) N={у|уÎ Z, -4≤ у≤ 5}; в) К ={z|zÎ R, -7≤ z< 0}. Изобразите множества М, N, К на числовой прямой.
2Б. А – множество правильных многоугольников, В – множество треугольников, С – множество четырехугольников. Постройте круги Эйлера для множеств А, В и С. Укажите характеристические свойства множеств: а) АÇ В; б) АÇ С; в) ВÇ С; г) АÇ ВÇ С.
3А. Изобразите следующие множества на числовой прямой и задайте их описанием характеристического свойства: а) А=[-1; 4]; б) В=(-3; 1); в) С=[2; +∞).
3Б. Пусть А={10, 11, 12, 13, 14, 15, 16}, В={13, 15, 17}. В каком отношении находятся множества А и В? Изобразите множества А и В на кругах Эйлера. Найдите А\В, В\А. Верно ли утверждение: А\В=В\А?
4А. Прочтите записи и изобразите на числовой прямой следующие множества: а) А={х|хÎ R, -5≤ х≤ 1}; б) В={у|уÎ N, -1≤ у< 7}; в) С={z|zÎ Z, z≥ -3}.
4Б. Даны множества: Е={1, 2, 5, 6}, F={3, 4, 5, 6}. В каком отношении находятся множества Е и F? Изобразите их на кругах Эйлера. Найдите ЕÈ F, ЕÇ F. Верны ли утверждения: а) 1Î ЕÈ F; б) 1Î ЕÇ F; в) 5Î ЕÈ F; г) 5Î ЕÇ F; д) 7Î ЕÈ F?
5А. Прочтите записи и изобразите на числовой прямой следующие множества: а) L={х|хÎ N, х< 8}; б) Q={х|хÎ R, х> 3, 2}; в) R={ х|хÎ Z, -2≤ х≤ 2}.
5Б. Известно, что Р – множество двузначных натуральных чисел, S – множество всех нечетных натуральных чисел. Изобразите данные множества на кругах Эйлера. Из каких чисел состоит множество К=РÇ S? Запишите множество К двумя способами. Верно ли, что а) 21Î К; б) 32Î К; в) 7Ï К; г) 17Ï К.
0А. Прочтите записи и изобразите на числовой прямой множества: а) Т={х|хÎ Nо, |х|< 2}; б) S={х|хÎ Z, -2< х≤ 3}; в) U={х|хÎ R, х< -7}
Решение: а) Т={х|хÎ Nо, |х|< 2} Множество Т состоит из элементов х, таких, что х – натуральное число, меньшее 2.
0Б. А – множество параллелограммов, В – множество прямоугольников, С – множество четырехугольников. Постройте круги Эйлера для множеств А, В, С. Укажите характеристическое свойство множеств: а) АÇ В, б) АÇ С, в) ВÇ С, г) АÇ ВÇ С. Решение: а) устанавливаем, множества А, В и С находятся в отношении включения, а именно В Ì А Ì С.
в) находим А Ç С.
г) находим В Ç С.
д) находим А Ç В Ç С.
ТЕОРИЯ МНОЖЕСТВ (задания ІІІ уровня)
1А. Даны множества: А – множество студентов университета, В – множество студентов дневного отделения, С – множество студентов-заочников, Д – множество студентов психолого-педагогического факультета, Е – множество студентов, изучающих английский язык. Изобразите данные множества и отношения между ними с помощью кругов Эйлера.
1Б. Найдите АÈ В, АÇ В, А\В, В\А, если: а) А=(3, 8], В=(-1; +∞); б) А={х|х< 18, хÎ Nо}, В={х||х|< 4, хÎ Z}; в) А – множество равнобедренных треугольников, В – множество прямоугольных треугольников. Изобразите полученные множества на числовой прямой (где это возможно).
2А. Даны множества: А – множество учащихся школы,
2Б. Найдите АÈ В, АÇ В, А\В, В\А, если: а) А=(-1, 5) В=[0, 4]; б) А={х|хÎ R, 1≤ х< 3}, В={х|хÎ R, 3≤ х< 5}; в) А – множество всех прямоугольников, В – множество всех ромбов. Изобразите полученные множества на числовой прямой (где это возможно).
3А. Известно, что Р, Q, S – подмножества универсального множества. Изобразите на кругах Эйлера множества: а) (Р\Q)'Ç S; б) (QÇ Р)'\ S; в) (РÇ Q)Ç S'. Для каждого пункта сделайте свой чертеж.
а) М'Ç (LÈ R); б) М'\ (LÇ R); в) (LÇ R)'\ (R\M). Для каждого пункта сделайте свой чертеж.
4Б. Считая множество R универсальным, найдите дополнения до R следующих множеств: а) Р={х||х|≤ 6, хÎ R}; б) Q={у|-∞ < у< 0, уÎ R}; в) S={z|z> 10, zÎ R}. Изобразите множества Р, Q, S и Р', Q', S' на числовой прямой.
5А. Известно, что А, В, D – подмножества универсального множества. Изобразите на кругах Эйлера множества:
б) (В|D)'Ç А; в) (А'È В')Ç D.
5Б. Найдите множества АÈ В, АÇ В, А\В, В\А, если: а) А=(0, +∞), В = [-4, 6]; б) А={х|хÎ R, 2≤ х≤ 5}, В={х|хÎ R, 5≤ х< 8}; в) А – множество прямоугольных треугольников, В – множество равнобедренных треугольников. Изобразите полученные множества на числовой прямой (где это возможно).
а) (АÈ С)Ç К; б)А'Ç С; в) (А'Ç К) È С.
Решение: а) (АÈ С)Ç К
2) (АÈ С)Ç К
б)А'Ç С
2) А'Ç С º
в) (А'Ç К) È С
2) А'Ç К \\\ 3) (А'Ç К) È С
0Б. Найдите и покажите на числовой прямой множества а)А'; б)(АÈ В)'; в)(А\В)', г)А'È В', если А={х||х|< 2, хÎ R}. В={у|3< х< +∞, хÎ R}. Решение: изобразим на числовой прямой множества А и В
1А. На координатной плоскости постройте прямую, параллельную оси (ОУ) и проходящую через точку А(-2, 3). Декартово произведение каких двух множеств изображается на координатной плоскости в виде этой прямой. Рассмотрите случай, когда прямая параллельна оси (ОХ).
1Б. Даны множества А={х|-8≤ х< 3, хÎ R}, В={х|0< х≤ 7, хÎ R},
2А. На координатной плоскости постройте прямоугольник, вершинами которого являются точки А(-2, 6), В(-2, -1), С(5, 6), Д(5, 1). Задайте построенное множество точек в виде декартового произведения.
2Б. Даны множества А=(-∞, 0), В=[2, 6], С=(-3, 10). Запишите и покажите на числовой прямой множества: а) АÈ С\В; б) АÈ (С\В)'; в) В'Ç (АÈ С); г) (В\А)'Ç С.
3А. Декартово произведение множеств Х и У задано множеством точек в прямоугольной системе координат. Запишите множества Х и У.
3Б. Даны множества: А={х|-3< х< ∞, хÎ R}, В={х|-10≤ х< 9, хÎ R}, С={х| |х|< 4, хÎ R}. Запишите и покажите на числовой прямой множества: а) А\СÈ В; б) АÇ С'Ç В'; в) А'È (В\С)'; г) (АÈ В)'\(ВÇ С)'.
4А. Декартово произведение множеств Х и У задано множеством точек в прямоугольной системе координат. Запишите множества Х и У.
-1 0 1 2 3 4 х 0 х -2
4Б. Даны множества: А=[-9, 3), В=[1, +∞), С=(0, 4). Запишите и покажите на числовой прямой множества: а) (В\А)Ç С, б) (А\В')Ç С, в) (АÈ В)'\С', г) (А\В)'È (АÈ С)'.
5А. Декартово произведение множеств Х и У задано множеством точек в прямоугольной системе координат. Запишите множества Х и У. а) у б) у
5Б. Даны множества: А={х|0£ х< 5, хÎ R}, В={х|0£ х+∞, хÎ R}, С={х|–-∞ < х£ 0, хÎ R}. Запишите и покажите на числовой прямой множества: а) А\В\С; б) АÇ В'; в) А'Ç (В\С); г) (АÇ В)'\С'.
ТЕОРИЯ МНОЖЕСТВ (задания V уровня)
1А. Докажите двумя способами, что для любых множеств А, В, С справедливы равенства: А\(ВÇ С)=(А\В)È (А\С).
1Б. Выбрано некоторое множество, состоящее из натуральных чисел. Известно, что среди них имеется 100 чисел, кратных двум; 115 чисел, кратных трем; 120 чисел, кратных пяти; 45 чисел, кратных шести; 38 чисел, кратных десяти; 50 чисел, кратных пятнадцати; 20 чисел, кратных тридцати. Определите, сколько элементов в заданном множестве.
2А. Докажите двумя способами, что для любых множеств А, В, С справедливы равенства: А\(ВÈ С)=(А\В)Ç (А\С).
2Б. Из 75 учащихся музыкального училища 30 умеют играть на баяне, 25 – на гитаре и 36 – балалайке. На баяне и гитаре умеют играть 7, на гитаре и балалайке – 9, на баяне и балалайке 13 человек. На всех трех инструментах играет 3 человека. Найдите: а) сколько человек умеет играть только на одном инструменте; б) сколько учащихся не играет ни на одном из вышеназванных инструментов.
3А. Докажите двумя способами, что для любых множеств А, В, С справедливы равенства: АÈ (ВÇ С)=(АÈ В)Ç (АÈ С).
3Б. Для того, чтобы написать заметку в стенгазету, студент взял в деканате следующие сведения: из 40 студентов 25 человек не имеют «троек» по педагогике, 28 – по математике, 31 – по психологии, 22 – по математике и психологии, 16 – по математике и педагогике, 16 – по психологии и педагогике, 12 человек учатся без «троек». Прочитав заметку, редактор сказал: «Данные явно неверные». Объясните, почему представленные сведения не могут быть верными.
4А. Докажите двумя способами, что для любых множеств А, В, С справедливы равенства: (А\В)'=А'È (АÇ В).
4Б. В бригаде 19 рабочих. Из них 9 токарей, 10 слесарей, 8 электросварщиков; 4 токаря могут работать слесарями, 3 токаря и 2 слесаря – электросварщиками. Сколько членов бригады владеет тремя специальностями?
5А. Докажите двумя способами, что для любых множеств А, В, С справедливы равенства: А'È (ВÈ С)'= (АÇ В)'Ç (АÇ С)'.
5Б. Из 100 студентов английский язык изучают 28 человек; немецкий – 30; французский – 42; английский и немецкий – 5; все три языка изучают 3 студента. Определите, сколько студентов не изучают ни одного языка? Сколько студентов изучают только один язык?
|

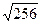 ,
,  ,
,  ,
,  } и В={12, 22, 32, 42}.
} и В={12, 22, 32, 42}. г)
г)








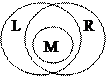 4А. Пусть L, R, M – подмножества универсального множества. Изобразите на кругах Эйлера множества:
4А. Пусть L, R, M – подмножества универсального множества. Изобразите на кругах Эйлера множества: а) (В|А)Ç D';
а) (В|А)Ç D'; 0А. Пусть А, С, К - подмножества универсального множества. Изобразите на кругах Эйлера множества:
0А. Пусть А, С, К - подмножества универсального множества. Изобразите на кругах Эйлера множества:




 2, х
2, х  -2, хÎ R}
-2, хÎ R}

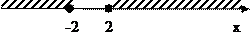

 y
y а) б) 3
а) б) 3





 -2 2 х
-2 2 х

 у у
у у


 а) 3 б)
а) 3 б)




 -1- 1- х
-1- 1- х х 0 1
х 0 1 0 1 2 6
0 1 2 6


