Задание №1
£ 0, 2 и 5 £ 0, 8 и 1, 25 £ 0, 8 и 5 £ 0, 2 и 1, 25
РЕШИТЕ ЗАДАЧИ: Задача 1. Недельный доход, равный 40 ден. ед., субъект расходует на хлеб и молоко. Если цена буханки хлеба равна 4 ден. ед., а цена 1 литра молока составляет 10 ден. ед., каково уравнение бюджетной линии? Как изменится уравнение бюджетной линии, если доход субъекта снизится до 20 ден. ед.? Сколько буханок хлеба смог бы купить субъект, если бы он отказался от покупки молока?
Задача 2. Найти предельную норму замещения товара Y товаром Х при переходе от набора В к набору С.
Задача 3.. Располагаемый доход домохозяйств в первом году составил 2.000 ед. Домохозяйства тратят на потребительские расходы 1.800 ед., а сберегают 200 ед. При увеличении во втором году дохода до 2.500 ед. потребление составили 2.200 ед., а сбережения – 300 ед. Найдите среднюю склонность к потреблению и среднюю склонность к сбережению в первом и втором годах, а также предельную склонность к потреблению и предельную склонность к сбережению.
Задача 4. Недельный доход, равный 120 ден. ед., субъект расходует на хлеб и молоко. Если цена буханки хлеба равна 10 ден. ед., а цена 1 литра молока составляет 40 ден. ед., каково уравнение бюджетной линии? Как изменится уравнение бюджетной линии, если доход субъекта возрастет до 200 ден. ед.? Сколько литров молока смог бы купить субъект, если бы он отказался от покупки хлеба?
Предисловие Учебно-методическое пособие подготовлено в соответствии с учебной программой курса «Топография с основами геодезии», утвержденной Министерством образования Республики Беларусь и Государственным стандартом образования Республики Беларусь для студентов географических специальностей вузов. Настоящее пособие направлено на закрепление теоретического курса и предназначено к выполнению комплекса камеральных работ для составления топографического плана. Данное пособие предусматривает выполнение лабораторного практикума по трем заданиям: Уравнивание и вычисление координат точек замкнутого теодолитного хода; математическая обработка результатов тахеометрической съемки и составление топографического плана с нанесением географических объектов и ситуации местности в системе принятых условных обозначений. Пособие содержит подробные методические указания с необходимыми расчетными формулами и решением примера. Всего разработано 60 вариантов для выполнения лабораторных работ и КСР по изучаемой теме. Тема 6. Математическая обработка теодолитного хода. Составление топографического плана по результатам тахеометрической съемки Цель задания – выполнить математическую обработку топографо-геодезических измерений и составить топографический план участка местности в заданном масштабе. Для выполнения крупномасштабной топографической съемки производятся полевые геодезические измерения по созданию планового и высотного съемочного обоснования с целью достижения необходимой плотности пунктов геодезических сетей. Основным методом построения планового обоснования является проложение теодолитных ходов с последующим вычислением координат точек. Высотное съемочное обоснование создается методом геометрического нивелирования, для чего, определяются отметки высот точек существующего планового съемочного обоснования. Теодолитные ходы представляют собой системы ломаных линий, в которых измеряются горизонтальные углы на поворотных точках хода и длины линий между этими точками. При углах наклона линий по отношению к горизонтальной плоскости более 1, 5° измеряются вертикальные углы для введения поправок за наклон линий и вычисляются их горизонтальные проложения. Теодолитные ходы прокладываются между геодезическими пунктами с известными координатами, которые служат исходными пунктами. В случае отсутствия исходных геодезических пунктов на участки местности площадью до 1 км2 могут создаваться самостоятельные съемочные сети в своей условной системе координат. Различают следующие виды теодолитных ходов: · Разомкнутый ход, начало и окончание которого опираются на два исходных пункта; · Замкнутый ход представляет собой многоугольник, опирающийся на один исходный пункт; · Висячий ход, один из концов которого примыкает к пункту геодезического обоснования. Проложение висячих теодолитных ходов допускается лишь в отдельных случаях, когда необходимо создать обоснование для съемки неответственных объектов. Тема данной лабораторной работы предусматривает выполнение следующих заданий: 1) уравнивание замкнутого теодолитного хода и вычисление прямоугольных координат точек хода в заданной условной системе координат; 2) математическую обработку результатов тахеометрической съемки; 3) составление топографического плана участка местности в заданном масштабе. Задание №1 Рассмотрим математическую обработку замкнутого теодолитного хода на примере, помещенном в таблице 1. Результаты полевых измерений в теодолитном ходе повариантно выписывают из приложения 1 «Исходные данные для уравнивания теодолитного хода» в соответствующие графы ведомости вычисления координат. 1. Уравнивание измеренных углов состоит из: · вычисления суммы измеренных углов ∑ β изм. = 359°58, 5′ (см. табл.1); · определения теоретической суммы углов по формуле ∑ β теор. = 180°(n -2), где n – число углов в ходе (в рассматриваемом примере ∑ β теор. = 180°(4-2) = 360°00′); · вычисления фактической угловой невязки по формуле f β = ∑ β изм.-∑ β теор.; f β = 359°59′ - 360°00′ = - 0°01′. · определения величины допустимой угловой невязки согласно формуле f β доп. = Вычисленная фактическая угловая невязка не должна быть больше допустимой. В противном случае, если фактическая угловая невязка превышает значение допустимой невязки, то проверяются все вычисления. Если вычисления верны, то ошибка была допущена при измерении углов в полевых условиях. Необходимо вторично измерить углы в которых имеются короткие линии хода, а затем углы, которые измерялись в неблагоприятных условиях. Фактическая невязка распределяется с обратным знаком в виде поправок в измеренные значения углов. Вначале вводятся поправки в углы, имеющие доли минут, округляя их до целых минут. Бо́ льшие поправки необходимо вводить в углы с короткими сторонами. Сумма поправок должна равняться невязке с обратным знаком. Исправленные значения углов получают прибавлением поправок к измеренным углам. Контролем уравнивания служит получение теоретической суммы углов хода. 2. Вычисление магнитных азимутов А (или дирекционных углов α) сторон теодолитного хода. Исходный магнитный азимут измеряют непосредственно на местности при проложении теодолитного хода с применением ориентир-буссоли. В рассматриваемом примере исходный магнитный азимут Ам направления 101 – 102 равен 358°22΄. Вычисляют магнитные азимуты всех остальных сторон хода по формуле: А102-103 = 358°22΄ + 180° - 90°23΄ = 87°59΄. Контролем вычислений магнитных азимутов является получение значения исходного магнитного азимута А101-102 = 267°56΄ + 180° - - 89°34΄ = 358°22΄. Значения магнитных азимутов и исходных координат пунктов приведены по каждому варианту в приложении 1 с индексами «а», «б», «в», «г», «д». Для выполнения задания следует выбрать свой вариант с соответствующим индексом. 3. Вычисление горизонтальных проложений S выполняется только для линий, имеющих угол наклона n более 1, 5° по формуле S = L · cos ν, где L – длина линии, измеренная на местности, ν – угол наклона. Результаты вписывают в соответствующую графу ведомости вычисления координат. Если сторона теодолитного хода располагается на волнистом склоне, т.е. измеряемая линия имеет различные углы наклона, то горизонтальное проложение этой линии будет равно сумме всех исправленных за наклон отрезков составляющих данную линию (т.е. горизонтальное проложение вычисляется для каждого отдельного отрезка линии с учетом измеренных углов наклона каждого отрезка). 4. Вычисление приращений координат Δ x и Δ y выполняют по формулам прямой геодезической задачи Δ x = S · cos A и Δ y = S· sinA. В замкнутом теодолитном ходе алгебраические суммы приращений координат должны равняться нулю: fх =å Δ х = - 0, 25 м; fу =å Δ у = 0, 03 м (табл.1). Абсолютную линейную невязку вычисляют по формуле Абсолютная невязка характеризует точность выполненных полевых работ, ее величина не должна превышать допустимую f абс.£ f абс. доп.= = 0, 6 мм М, где М – знаменатель масштаба съемки. Для определения допустимости абсолютной невязки и оценки точности выполненных полевых работ вычисляют также относительную невязку, т.е. отношение абсолютной невязки f абс. к периметру полигона (хода) ∑ S: Допустимость невязки определяется заданной точностью и условиями местности и изменяется от 1/1000 – при неблагоприятных условиях измерений; 1/2000 – при средних условиях и 1/3000 – при благоприятных условиях измерений. В случае допустимости полученной фактической абсолютной невязки, величины невязок fx и fy распределяются с обратным знаком пропорционально длинам сторон теодолитного хода. Для этого определяют долю поправки на каждые 100 м периметра полигона. Каждую из невязок fx и fy делят на значение длины полигона в сотнях метров и вычисляют поправки в каждое приращение пропорционально длине соответствующей линии. То есть в более длинную линию будет вводиться поправка, имеющая большее значение. Поправки вводят со знаком обратным знаку невязки. Сумма поправок должна равняться невязке с обратным знаком. Поправки вводят в вычисленные приращения и получают исправленные приращения координат. Контроль уравнивания приращений в замкнутом теодолитном ходе – å Δ х уравн. = 0; å Δ у уравн. = 0. Для вычисления координат точек теодолитного хода необходимо знать координаты исходного пункта. Если они не известны, то задаются условно. Координатами исходного пункта № 101 в нашем примере являются: Х 101 = 1020, 00 м; Y 101 = 1085, 00 м. Координаты остальных точек теодолитного хода вычисляются в следующем порядке: координата последующей точки равна координате предыдущей точки плюс исправленное приращение между этими точками:
Координаты последующей точки хода № 102 будут равны: Х 102 = Х 101 + Δ Х испр. = 1020, 00 + 280, 06 = 1300, 06 м Y 102 = Y 101 + Δ Y испр. = 1085, 00 + (- 7, 99) = 1077, 01 м. Контролем вычисления координат в замкнутом теодолитном ходе является получение координат исходного пункта.
|

 , где n – число углов в ходе (в рассматриваемом примере
, где n – число углов в ходе (в рассматриваемом примере  доп. =
доп. =  = ±3′).
= ±3′). . То есть, магнитный азимут направления 102 – 103 будет равен значению магнитного азимута предыдущего направления
. То есть, магнитный азимут направления 102 – 103 будет равен значению магнитного азимута предыдущего направления  плюс 180° и минус исправленный угол между этими направлениями
плюс 180° и минус исправленный угол между этими направлениями  .
.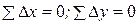 . Но вследствии погрешностей при определении S эти суммы отличаются от нуля, образуя линейные невязки приращений координат fх и fу. В рассматриваемом примере
. Но вследствии погрешностей при определении S эти суммы отличаются от нуля, образуя линейные невязки приращений координат fх и fу. В рассматриваемом примере , которая равна
, которая равна 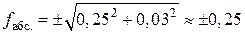 м.
м. . В рассматриваемом примере относительная невязка будет равна:
. В рассматриваемом примере относительная невязка будет равна: 

 .
.


