Проверка на прочность поперечной балки
Поперечная балка испытывает деформацию изгиба. Выполним ее проверку на прочность. Расчетная схема дана на рисунке 3.3. Проверку на прочность производим по условию
где
Wz – осевой момент сопротивления поперечного сечения, м3;
Для материала Сталь 3 принимаем
Максимальный изгибающий момент для данного вида нагружения определяется по формуле
где R1 и l1 – указаны на рисунке 3.3.
Рис.3.3. Расчетная схема для проверки на прочность поперечной балки Величину реакции R1 найдём из системы двух уравнений R1 + R2 = Q (3.25) R1 l1 = R2 l2 Решая систему из двух уравнений, получим R1 = Q l1/ (l1 + l2) (3.26) Подставив в уравнение указанные величины получим значение R1. Момент сопротивления для полого прямоугольного сечения балки определяется по выражению Wz = где h, h1, в, в1 – размеры сечения балки в соответствии с рисунком 3.4.
Рис. 3.4. Схема сечения поперечной балки Подставив в уравнения (3.23), (3.24), (3.27) значения указанных величин, получим величину максимального напряжения изгиба. Условие прочности для поперечной балки соблюдается, если оно не превышает допустимое в соответствии с (3.23).
3.4. Определение параметров электродвигателя Скорость подъема U указана в индивидуальном задании. Частота вращения винта
где Р – шаг резьбы. Задаваясь частотой вращения ротора электродвигателя 750, 1000, 1500 или 3000 об/мин, определяют передаточное число от электродвигателя к винту
Если i ≥ 4, можно использовать для передачи момента от электродвигателя к винту клиноременную передачу. В противном случае необходимо подобрать редуктор. Определим требуемую мощность двигателя по формуле
где Nм – требуемая мощность для подъема груза, Вт;
Требуемую мощность для для подъема груза находим по формуле Nм = U ∙ Fa (3.31) где U – скорость подъема груза, м/с; Fa – вес автомобиля, Н. Принимаем скорость подъема груза указанной в задании. Общий КПД
где
Подставив в формулу (3.32) значения указанных величин, получим значение Принимаем, например, электродвигатель с частотой вращения nдв= 1390 мин-1. Далее определяем передаточное отношение от электродвигателя к грузовому винту по формуле
где nдв – частота вращения вала электродвигателя, в нашем примере nдв = 1390 мин-1; nв – частота вращения грузового винта, мин-1. Частоту вращения грузового винта найдем по выражению
где U – скорость подъема груза; р – шаг резьбы; nр – число заходов резьбы, nр = 1. Подставив в формулу (3.33) значение указанных величин, получим передаточное отношение от электродвигателя к грузовому винту. Зная необходимую мощность и передаточное отношение, выбираем по справочнику соответствующий мотор-редуктор. Если фактическое передаточное отношение отличается от расчетного, то необходимо пересчитать фактическую частоту вращения винта nв.ф и фактическую скорость подъема U используя формулы (3.33) и (3.34). Фактическое время подъема tп будет равно
где L – полная высота подъема. Контрольные вопросы 1. Как определяется КПД винтовой пары? 2. Как проверить условие самоторможения винта? 3. Как определяется приведенное напряжение действующее на винт? 4. В каких случаях выполняется проверочный расчет винта на продольный изгиб? 5. Как определяется число витков в гайке? 6. Как определяется наружный диаметр гайки? 7. Как выполняется проверка на прочность поперечной балки? 8. Как определяется мощность электродвигателя? 9. Как определяется общий КПД подъемника? 10. Как определяется передаточное отношение от электродвигателя к грузовому винту?
Варианты заданий Таблица 1.2 Исходные данные
|

 (3.23)
(3.23) – максимальное напряжение изгиба в балке, МПа;
– максимальное напряжение изгиба в балке, МПа; – максимальный изгибающий момент, Н · м;
– максимальный изгибающий момент, Н · м; – допускаемое напряжение изгиба, МПа.
– допускаемое напряжение изгиба, МПа.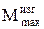 = R1 l1 (3.24)
= R1 l1 (3.24)
 (3.27)
(3.27)
 . (3.28)
. (3.28) . (3.29)
. (3.29) (3.30)
(3.30) – общий КПД привода.
– общий КПД привода. =
=  (3.32)
(3.32) – КПД подшипников качения,
– КПД подшипников качения,  – КПД цепной или клиноремённой передачи,
– КПД цепной или клиноремённой передачи,  – КПД самотормозящейся передачи винт-гайка, определённый по формуле (3.4);
– КПД самотормозящейся передачи винт-гайка, определённый по формуле (3.4); – КПД редуктора,
– КПД редуктора,  (3.33)
(3.33) (3.34)
(3.34) 3.35)
3.35)


