Преобразование поворота и отражения
Общую матрицу 2х2, которая осуществляет вращение фигуры относительно начала координат, можно получить из рассмотрения вращения единичного квадрата вокруг начала координат.
Как следует из рисунка, точка В с координатами (1, 0) преобразуется в точку В *, для которой х *= (1) cosq и y =(1) sinq, а точка D, имеющая координаты (0, 1) переходит в точку D * с координатами x *=(-1) sinq и y *=(1) cosq. Матрица преобразования общего вида записывается так:
Для частных случаев. Поворот на 900 можно осуществить с помощью матрицы преобразования
Если использовать матрицу координат вершин, то получим, например:
Поворот на 1800 получается с помощью матрицы В то время как чистое двумерное вращение в плоскости xy осуществляется вокруг оси, перпендикулярной к этой плоскости, отображение определяется поворотом на 1800 вокруг оси, лежащей в плоскости ху. Такое вращение вокруг линии у=х происходит при использовании матрицы Преобразованные новые выражения определяются соотношением:
Вращение вокруг у = 0 получается при использовании матрицы
|


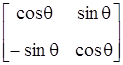 .
. .
. .
. .
. .
. .
. .
.


