Однородные координаты
Преобразования переноса, масштабирования и поворота записываются в матричной форме в виде
Очевидно, что перенос, в отличие от масштабирования и поворота, реализуется с помощью сложения. Это обусловлено тем, что вводить константы переноса внутрь структуры общей матрицы размера 2х2 не представляется возможным. Желательным является представление преобразований в единой форме – с помощью умножения матриц. Эту проблему можно решить за счет введения третьей компоненты в векторы точек
Используя эту матрицу, получаем преобразованный вектор [ х* у* 1]. Добавление третьего элемента к вектору положения и третьего столбца к матрице преобразования позволяет выполнить смещение вектора положения. Третий элемент здесь можно рассматривать как дополнительную координату вектора положения. Итак, вектор положения [ х у 1] при воздействии на него матрицы 3х3 становится вектором положения в общем случае вида [ X Y Н]. Представленное преобразование было выполнено так, что [X Y Н ]= [ х* у* 1]. Преобразование, имеющее место в трехмерном пространстве, в нашем случае ограничено плоскостью, поскольку H = 1. Если, однако, третий столбец Плоскость, в которой теперь лежит преобразованный вектор положения, находится в трехмерном пространстве. Преобразованные обычные координаты получаются за счет нормализации однородных координат, т. е.
Геометрически все преобразования х и у происходят в плоскости Н= 1 после нормализации преобразованных однородных координат. Преимущество введения однородных координат проявляется при использовании матрицы преобразований общего вида порядка 3х3
с помощью которой можно выполнять и другие преобразования, такие как смещение, операции изменения масштаба и сдвига, обусловленные матричными элементами а, b, с и d. Указанные операции рассмотрены ранее. Основная матрица преобразования размера 3х3 для двумерных однородных координат может быть подразделена на четыре части:
Как мы видим, а, b, с и d осуществляют изменение масштаба, сдвиг и вращение; т и п выполняют смещение, а р и q – получение проекций. Оставшаяся часть матрицы, элемент s, производит полное изменение масштаба. Чтобы показать это, рассмотрим преобразование
Здесь Х = х, Y = у, а Н = s. Это дает х * = x / s и y * == y / s. В результате преобразования [ х у 1 ] —> [ x / s y / s 1] имеет место однородное изменение масштаба вектора положения. При s < 1 происходит увеличение, а при s > 1 уменьшение масштаба.
|

 ,
,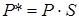 ,
, .
. и
и  , т.е. представляя их в виде
, т.е. представляя их в виде  и
и  . Матрица преобразования после этого становится матрицей размера 3х3, например:
. Матрица преобразования после этого становится матрицей размера 3х3, например: .
. матрицы преобразования Т размера 3х3 отличен от 0, то в результате матричного преобразования получим [ х у 1] × Т = [ Х Y Н ], где Н ¹ 1.
матрицы преобразования Т размера 3х3 отличен от 0, то в результате матричного преобразования получим [ х у 1] × Т = [ Х Y Н ], где Н ¹ 1. и
и  .
. ,
, .
.



