Исследование линейной непрерывной САУ
Исходные данные
Структура исследуемой замкнутой линейной непрерывной САУ представлена на рисунке 2, где  – управляющее воздействие, – управляющее воздействие,  – возмуща-ющее воздействие, – возмуща-ющее воздействие,  – сигнал ошибки, – сигнал ошибки,  – выходной сигнал. – выходной сигнал.
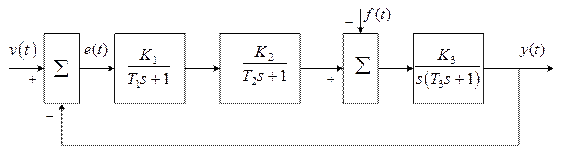
Рисунок 2
Значения параметров Т 1, Т 2, Т 3 заданы в таблице 3. Размерность Т 1, Т 2, Т 3 в секундах, общий коэффициент передачи  имеет размерность 1/с, в таблице 3 заданы также желаемые показатели качества системы: максимальная ошибка по скорости еск при скачке по скорости имеет размерность 1/с, в таблице 3 заданы также желаемые показатели качества системы: максимальная ошибка по скорости еск при скачке по скорости  и f = 0, время переходного процесса tp в секундах, и перерегулирование и f = 0, время переходного процесса tp в секундах, и перерегулирование  в процентах. в процентах.
Таблица 3
| Номер варианта
| 
| еск
| 
| y, %
| T 1× 10-1
| T 2× 10-1
| T 3
| |
| 2, 5
| 0, 1
| 3, 0
|
| 0, 55
| 1, 9
| 1, 8
| |
| 2, 0
| 0, 08
| 3, 1
|
| 0, 3
|
|
| |
| 3, 0
| 0, 15
| 3, 5
|
| 0, 5
| 1, 2
| 1, 4
| |
| 1, 8
| 0, 06
| 5, 0
|
| 0, 6
|
| 3, 5
| |
| 3, 3
| 0, 15
| 4, 0
|
| 0, 57
| 1, 5
|
| |
| 3, 2
| 0, 14
| 3, 0
|
| 0, 4
|
|
| |
| 1, 6
| 0, 08
| 2, 5
|
| 0, 5
| 1, 9
|
| |
| 1, 8
| 0, 07
| 1, 5
|
| 0, 58
|
|
| |
| 1, 2
| 0, 05
| 2, 0
|
| 0, 48
|
|
| |
| 1, 4
| 0, 04
| 2, 5
|
| 0, 33
| 1, 9
|
| |
| 1, 9
| 0, 06
| 3, 0
|
| 0, 63
| 1, 2
|
| |
| 2, 3
| 0, 08
| 3, 5
|
| 0, 34
| 2, 3
| 4, 5
| |
| 2, 7
| 0, 1
| 4, 0
|
| 0, 49
| 1, 1
| 1, 5
| |
| 2, 6
| 0, 08
| 3, 5
|
| 0, 34
| 1, 6
|
| |
| 2, 8
| 0, 06
| 3, 8
|
| 0, 23
|
| 4, 8
| |
| 1, 5
| 0, 02
| 2, 5
|
| 0, 45
| 0, 5
| 1, 8
| |
| 3, 5
| 0, 1
| 2, 0
|
| 1, 2
|
| 1, 8
| |
| 3, 2
| 0, 08
| 1, 5
|
| 1, 4
| 2, 4
| 2, 1
| |
| 2, 8
| 0, 1
| 3, 0
|
| 0, 15
| 2, 8
| 3, 6
| |
| 2, 5
| 0, 1
| 4, 2
|
| 0, 48
| 2, 3
| 1, 7
| |
| 1, 4
| 0, 06
| 2, 5
|
| 0, 27
|
| 2, 4
| |
| 1, 6
| 0, 06
| 2, 5
|
| 0, 33
| 3, 5
| 4, 3
| |
| 1, 8
| 0, 05
| 4, 0
|
| 0, 1
| 1, 8
| 1, 1
| |
| 2, 6
| 0, 08
| 3, 0
|
| 0, 56
| 2, 5
| 4, 9
| |
| 2, 8
| 0, 08
| 2, 8
|
| 0, 5
|
| 1, 6
| |
| 2, 4
| 0, 07
| 1, 5
|
| 0, 47
|
|
| |
| 3, 5
| 0, 1
| 3, 0
|
| 0, 5
| 2, 5
| 4, 2
| |
| 3, 7
| 0, 1
| 3, 2
|
| 0, 25
| 1, 2
| 3, 8
| |
| 3, 6
| 0, 11
| 2, 5
|
| 0, 34
| 1, 6
| 2, 4
| |
| 3, 8
| 0, 12
| 2, 4
|
| 0, 48
| 1, 8
| 2, 5
| Задание
1. Найти передаточные функции разомкнутой системы  ; замкнутой системы: главную передаточную функцию ; замкнутой системы: главную передаточную функцию  , по ошибке , по ошибке  и по возмущению и по возмущению  . .
2. Построить область устойчивости системы в плоскости общего коэффициента передачи  и постоянной времени и постоянной времени  при заданных значениях при заданных значениях  и и  . Найти граничное значение . Найти граничное значение  при заданном значении при заданном значении  , при котором система выходит на границу устойчивости. , при котором система выходит на границу устойчивости.
3. Построить графики логарифмических амплитудной и фазовой частотных характеристик  и и  при значении коэффициента передачи при значении коэффициента передачи  . .
4. Оценить запасы устойчивости по модулю  и фазе и фазе  , величину ошибки по скорости , величину ошибки по скорости  при при  , ,  , время переходного процесса , время переходного процесса 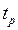 и перерегулирование и перерегулирование 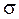 в исходной системе при в исходной системе при  . .
5. Если исходная система не удовлетворяет заданным в табл. 2 показателям качества  , ,  , еск (хотя бы одному из них) или имеет малые запасы , еск (хотя бы одному из них) или имеет малые запасы
устойчивости, то провести коррекцию системы (последовательного или
параллельного типа) и найти передаточную функцию корректирующего
устройства.
6. Вычислить в скорректированной системе переходный процесс на выходе  при подаче на вход единичной ступенчатой функции при подаче на вход единичной ступенчатой функции  (f = 0). Найти (f = 0). Найти  , ,  по переходному процессу и сравнить их с требуемыми по заданию. по переходному процессу и сравнить их с требуемыми по заданию.
Краткие методические указания
1. Передаточная функция разомкнутой системы  при при  ; главная передаточная функция ; главная передаточная функция  при при  ; передаточная функция по ошибке ; передаточная функция по ошибке  при при  и по возмущению и по возмущению  при при  определяются на основе правил структурных преобразований [1, с. 27-34]. определяются на основе правил структурных преобразований [1, с. 27-34].
2. Передаточная функция разомкнутой исходной системы имеет вид  , где , где  . Характеристическое уравнение замкнутой системы будет . Характеристическое уравнение замкнутой системы будет
 , ,
где при заданных из таблицы 3 числовых значениях 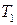 и и  , коэффициенты , коэффициенты  будут зависеть от параметров будут зависеть от параметров  и T 2. Применение критерия Гурвица [1, c. 47-50] к характеристическому уравнению четвертого порядка дает следующие условия устойчивости: и T 2. Применение критерия Гурвица [1, c. 47-50] к характеристическому уравнению четвертого порядка дает следующие условия устойчивости:  . .
Приравнивая в написанных соотношениях правые части нулю, получим в плоскости K и T 2 границы устойчивости, ограничивающие некоторую область устойчивости. При заданном  находим граничное значение находим граничное значение  коэффициента передачи K. коэффициента передачи K.
3. Полагая  находим выражение для находим выражение для  , ,  из из  при s = j ω. Строим графики логарифмических характеристик [1, с. 34]. при s = j ω. Строим графики логарифмических характеристик [1, с. 34].
4. Запасы устойчивости по модулю и фазе определяются из логарифмических характеристик: на частоте среза  определяют определяют  , а на частоте, при которой , а на частоте, при которой 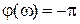 , находят , находят  . Величина ошибки по скорости . Величина ошибки по скорости  . Для ориентировочной оценки . Для ориентировочной оценки  и и  могут быть применены различные приближенные методы и формулы [1], либо следует построить переходной процесс могут быть применены различные приближенные методы и формулы [1], либо следует построить переходной процесс  при при  и из него определить и из него определить  и и  . В частности, можно воспользоваться следующим приемом. Найти вещественную частотную характеристику замкнутой системы . В частности, можно воспользоваться следующим приемом. Найти вещественную частотную характеристику замкнутой системы  , построить ее график в низкочастотной области и найти максимальное значение ординаты , построить ее график в низкочастотной области и найти максимальное значение ординаты  . Далее, зная . Далее, зная  и частоту среза и частоту среза  (находится из логарифмических характеристик) можно найти (находится из логарифмических характеристик) можно найти  и и  из диаграмм, связывающих из диаграмм, связывающих  и и  с величиной с величиной  [1, с. 78]. [1, с. 78].
5. Если исходная система не удовлетворяет заданным показателям качества, ее следует скорректировать. Различие методики коррекции приводятся в [1, 6]. В случае частотных методов синтеза коррекции строится желаемая ЛАЧХ  . В низкочастотной части желаемой ЛАЧХ при сохранении порядка астатизма требуемый коэффициент усиления выбирается из соотношения . В низкочастотной части желаемой ЛАЧХ при сохранении порядка астатизма требуемый коэффициент усиления выбирается из соотношения  . Частота среза при заданном . Частота среза при заданном  и и  выбирается по графику выбирается по графику
[1, с. 120]. На частоте среза желательно иметь наклон ЛАЧХ -20 дБ/дек с протяженностью этого участка не менее одной декады. Далее среднечастотная часть ЛАЧХ сопрягается с низкочастотной отрезком прямой с наклоном
(-40…-60) дБ/дек, а высокочастотные части желаемой и исходной ЛАЧХ по возможности должны совпадать.
Если найдена  , то в случае последовательной коррекции ЛАЧХ корректирующего устройства находится по выражению , то в случае последовательной коррекции ЛАЧХ корректирующего устройства находится по выражению 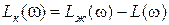 и далее по и далее по  находится передаточная функция корректирующего устройства находится передаточная функция корректирующего устройства  . Более подробно изложенная методика приведена в литературе [1, с. 118-122], [6, с. 355-360]. . Более подробно изложенная методика приведена в литературе [1, с. 118-122], [6, с. 355-360].
По логарифмическим частотным характеристикам следует для скорректированной системы найти запасы устойчивости по модулю и фазе. Считается, что приемлемыми на практике являются запасы устойчивости, лежащие в следующих пределах: по модулю  , по фазе , по фазе  . .
6. Так как практически любые методики синтеза САУ, в том числе и методика, изложенная выше, являются приближенными, то завершающим этапом синтеза является проверочный расчет для скорректированной системы, который заключается в построении кривой переходного процесса, т. е. изменения выходной координаты  при подаче на вход единичного ступенчатого сигнала при подаче на вход единичного ступенчатого сигнала  . По полученной переходной функции определяют для скорректированной системы величину . По полученной переходной функции определяют для скорректированной системы величину  и и  . .
В настоящее время наиболее приемлемый метод вычисления кривой
переходного процесса – это использование ЭВМ [1, с. 43].

Картограммы и картодиаграммы Картограммы и картодиаграммы применяются для изображения географической характеристики изучаемых явлений...
|

Практические расчеты на срез и смятие При изучении темы обратите внимание на основные расчетные предпосылки и условности расчета...
|

Функция спроса населения на данный товар Функция спроса населения на данный товар: Qd=7-Р. Функция предложения: Qs= -5+2Р,где...
|

Аальтернативная стоимость. Кривая производственных возможностей В экономике Буридании есть 100 ед. труда с производительностью 4 м ткани или 2 кг мяса...
|
Мелоксикам (Мовалис) Групповая принадлежность
· Нестероидное противовоспалительное средство, преимущественно селективный обратимый ингибитор циклооксигеназы (ЦОГ-2)...
Менадиона натрия бисульфит (Викасол) Групповая принадлежность
•Синтетический аналог витамина K, жирорастворимый, коагулянт...
Разновидности сальников для насосов и правильный уход за ними
Сальники, используемые в насосном оборудовании, служат для герметизации пространства образованного кожухом и рабочим валом, выходящим через корпус наружу...
|
СПИД: морально-этические проблемы Среди тысяч заболеваний совершенно особое, даже исключительное, место занимает ВИЧ-инфекция...
Понятие массовых мероприятий, их виды Под массовыми мероприятиями следует понимать совокупность действий или явлений социальной жизни с участием большого количества граждан...
Тактика действий нарядов полиции по предупреждению и пресечению правонарушений при проведении массовых мероприятий К особенностям проведения массовых мероприятий и факторам, влияющим на охрану общественного порядка и обеспечение общественной безопасности, можно отнести значительное количество субъектов, принимающих участие в их подготовке и проведении...
|
|

 – управляющее воздействие,
– управляющее воздействие,  – возмуща-ющее воздействие,
– возмуща-ющее воздействие,  – сигнал ошибки,
– сигнал ошибки,  – выходной сигнал.
– выходной сигнал.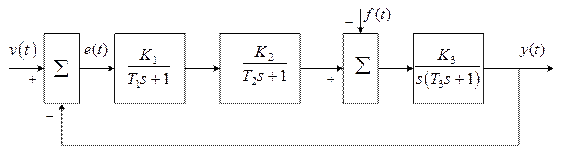
 имеет размерность 1/с, в таблице 3 заданы также желаемые показатели качества системы: максимальная ошибка по скорости еск при скачке по скорости
имеет размерность 1/с, в таблице 3 заданы также желаемые показатели качества системы: максимальная ошибка по скорости еск при скачке по скорости  и f = 0, время переходного процесса tp в секундах, и перерегулирование
и f = 0, время переходного процесса tp в секундах, и перерегулирование  в процентах.
в процентах.

 ; замкнутой системы: главную передаточную функцию
; замкнутой системы: главную передаточную функцию  , по ошибке
, по ошибке  и по возмущению
и по возмущению  .
. и постоянной времени
и постоянной времени  при заданных значениях
при заданных значениях  и
и  . Найти граничное значение
. Найти граничное значение  при заданном значении
при заданном значении  , при котором система выходит на границу устойчивости.
, при котором система выходит на границу устойчивости. и
и  при значении коэффициента передачи
при значении коэффициента передачи  .
. и фазе
и фазе  , величину ошибки по скорости
, величину ошибки по скорости  при
при  ,
,  , время переходного процесса
, время переходного процесса 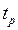 и перерегулирование
и перерегулирование 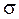 в исходной системе при
в исходной системе при  ,
,  при подаче на вход единичной ступенчатой функции
при подаче на вход единичной ступенчатой функции  (f = 0). Найти
(f = 0). Найти  при
при  ; главная передаточная функция
; главная передаточная функция  при
при  ; передаточная функция по ошибке
; передаточная функция по ошибке  при
при  при
при  определяются на основе правил структурных преобразований [1, с. 27-34].
определяются на основе правил структурных преобразований [1, с. 27-34]. , где
, где  . Характеристическое уравнение замкнутой системы будет
. Характеристическое уравнение замкнутой системы будет ,
,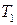 и
и  будут зависеть от параметров
будут зависеть от параметров  и T 2. Применение критерия Гурвица [1, c. 47-50] к характеристическому уравнению четвертого порядка дает следующие условия устойчивости:
и T 2. Применение критерия Гурвица [1, c. 47-50] к характеристическому уравнению четвертого порядка дает следующие условия устойчивости:  .
. находим выражение для
находим выражение для  ,
,  из
из  при s = j ω. Строим графики логарифмических характеристик [1, с. 34].
при s = j ω. Строим графики логарифмических характеристик [1, с. 34]. определяют
определяют 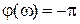 , находят
, находят  . Для ориентировочной оценки
. Для ориентировочной оценки  и
и  могут быть применены различные приближенные методы и формулы [1], либо следует построить переходной процесс
могут быть применены различные приближенные методы и формулы [1], либо следует построить переходной процесс  и из него определить
и из него определить  , построить ее график в низкочастотной области и найти максимальное значение ординаты
, построить ее график в низкочастотной области и найти максимальное значение ординаты  . Далее, зная
. Далее, зная  (находится из логарифмических характеристик) можно найти
(находится из логарифмических характеристик) можно найти  . В низкочастотной части желаемой ЛАЧХ при сохранении порядка астатизма требуемый коэффициент усиления выбирается из соотношения
. В низкочастотной части желаемой ЛАЧХ при сохранении порядка астатизма требуемый коэффициент усиления выбирается из соотношения  . Частота среза при заданном
. Частота среза при заданном  , то в случае последовательной коррекции ЛАЧХ корректирующего устройства находится по выражению
, то в случае последовательной коррекции ЛАЧХ корректирующего устройства находится по выражению 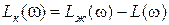 и далее по
и далее по  находится передаточная функция корректирующего устройства
находится передаточная функция корректирующего устройства  . Более подробно изложенная методика приведена в литературе [1, с. 118-122], [6, с. 355-360].
. Более подробно изложенная методика приведена в литературе [1, с. 118-122], [6, с. 355-360]. , по фазе
, по фазе  .
.


