Исходные данные
Структура нелинейной САУ представлена на рисунке 4, где НЭ- нелинейный элемент,  - передаточная функция непрерывной линейной части системы.
- передаточная функция непрерывной линейной части системы.

Рисунок 4
Передаточная функция  берется из пункта 3.1 как передаточная функция скорректированной системы с соответствующими числовыми коэффициентами. Нелинейный элемент НЭ имеет нелинейную характеристику
берется из пункта 3.1 как передаточная функция скорректированной системы с соответствующими числовыми коэффициентами. Нелинейный элемент НЭ имеет нелинейную характеристику 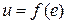 , которая для всех вариантов заданий является характеристикой идеального реле
, которая для всех вариантов заданий является характеристикой идеального реле
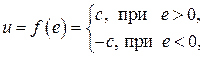
где величина  для вариантов заданий с 1 по 10 равна 1, с 11 по 20 равна 2, с 21 по 30 равна 3.
для вариантов заданий с 1 по 10 равна 1, с 11 по 20 равна 2, с 21 по 30 равна 3.
Задание
Используя метод гармонической линеаризации нелинейного элемента, определить на основе частотного способа возможность возникновения автоколебаний в замкнутой системе, их устойчивость, амплитуду и частоту.
Краткие методические указания
1. Методика определения автоколебаний частотным методом с использованием гармонической линеаризации изложена в [6, c. 596]. Приближенная передаточная функция нелинейного элемента для нашего случая (идеальное реле) имеет вид  , где
, где  - амплитуда искомого периодического режима,
- амплитуда искомого периодического режима,  .
.
2. На комплексной плоскости строится характеристика [  ] =
] =  . Это прямая, совпадающая с отрицательным отрезком действительной оси, вдоль которой идет оцифровка по амплитуде
. Это прямая, совпадающая с отрицательным отрезком действительной оси, вдоль которой идет оцифровка по амплитуде  . В том же масштабе на комплексной плоскости строится АФЧХ разомкнутой системы
. В том же масштабе на комплексной плоскости строится АФЧХ разомкнутой системы  при изменении частоты от 0 до
при изменении частоты от 0 до 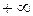 .
.
В точке пересечения АФЧХ  и прямой [
и прямой [  ] по графику
] по графику  находятся частота искомого периодического (гармонического) режима
находятся частота искомого периодического (гармонического) режима  , а на прямой [
, а на прямой [  ] в точке пересечения его амплитуда
] в точке пересечения его амплитуда  . Итак, в системе существуют периодические колебания
. Итак, в системе существуют периодические колебания  . Для определения устойчивости периодического режима можно воспользоваться следующим правилом: если при увеличении амплитуды
. Для определения устойчивости периодического режима можно воспользоваться следующим правилом: если при увеличении амплитуды  вдоль кривой [
вдоль кривой [  ] пересечение АФЧХ
] пересечение АФЧХ  происходит «изнутри наружу», то такой периодический режим будет устойчивым, т.е. в системе существуют автоколебания с частотой
происходит «изнутри наружу», то такой периодический режим будет устойчивым, т.е. в системе существуют автоколебания с частотой  и амплитудой
и амплитудой  .
.

 - передаточная функция непрерывной линейной части системы.
- передаточная функция непрерывной линейной части системы.
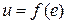 , которая для всех вариантов заданий является характеристикой идеального реле
, которая для всех вариантов заданий является характеристикой идеального реле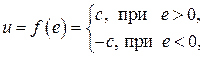
 для вариантов заданий с 1 по 10 равна 1, с 11 по 20 равна 2, с 21 по 30 равна 3.
для вариантов заданий с 1 по 10 равна 1, с 11 по 20 равна 2, с 21 по 30 равна 3. , где
, где  - амплитуда искомого периодического режима,
- амплитуда искомого периодического режима,  .
. ] =
] =  . Это прямая, совпадающая с отрицательным отрезком действительной оси, вдоль которой идет оцифровка по амплитуде
. Это прямая, совпадающая с отрицательным отрезком действительной оси, вдоль которой идет оцифровка по амплитуде  . В том же масштабе на комплексной плоскости строится АФЧХ разомкнутой системы
. В том же масштабе на комплексной плоскости строится АФЧХ разомкнутой системы  при изменении частоты от 0 до
при изменении частоты от 0 до 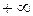 .
. ] по графику
] по графику  , а на прямой [
, а на прямой [  ] в точке пересечения его амплитуда
] в точке пересечения его амплитуда  . Итак, в системе существуют периодические колебания
. Итак, в системе существуют периодические колебания  . Для определения устойчивости периодического режима можно воспользоваться следующим правилом: если при увеличении амплитуды
. Для определения устойчивости периодического режима можно воспользоваться следующим правилом: если при увеличении амплитуды  и амплитудой
и амплитудой  .
.


