Как видим, при кручении деформации сдвига и касательные напряжения прямо пропорциональны расстоянию от центра тяжести сечения
Рис. 4.6. Эпюра касательных напряжений по поперечному сечению стержня представлена на рис. 4.5 справа. В центре тяжести круглого сечения касательные напряжения равны нулю. Наибольшие касательные напряжения будут в точках сечения, расположенных у поверхности стержня. Зная закон распределения касательных напряжений, легко определить их из условия, что крутящий момент в сечении представляет собой равнодействующий момент касательных напряжений в сечении:
где Подставив в (4.4) значение напряжений из формулы (4.3), получим
Имея в виду, что
где
Подставляя значение
Таким образом, окончательная формула для определения касательных напряжений при кручении имеет вид
Как видно из этой формулы, в точках одинаково удаленных от центра сечения, напряжения Наибольшие напряжения в точках у контура сечения:
Геометрическая характеристика Wp называется полярным моментом сопротивления или моментом сопротивления при кручении. Условие статической прочности вала при кручении имеет вид
здесь Кроме проверки прочности по этой формуле можно также подбирать диаметр вала или определять допускаемый крутящий момент при известных остальных величинах. Имея в виду, что для круглого сплошного сечения Wp = 0, 2d3, получаем
Допускаемый из условия – прочности крутящий момент определяют по формуле
|


 (4.4)
(4.4)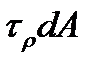 - элементарный крутящий момент внутренних сил, действующих на площадке dA.
- элементарный крутящий момент внутренних сил, действующих на площадке dA. . (4.5)
. (4.5) (4.6)
(4.6) - полярный момент инерции сечения, получим
- полярный момент инерции сечения, получим (4.7)
(4.7) в формулу (4.3), имеем
в формулу (4.3), имеем (4.8)
(4.8) (4.9)
(4.9) одинаковы.
одинаковы. (4.10)
(4.10) (4.11)
(4.11)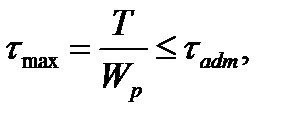 (4.12)
(4.12) - допускаемое касательное напряжение.
- допускаемое касательное напряжение.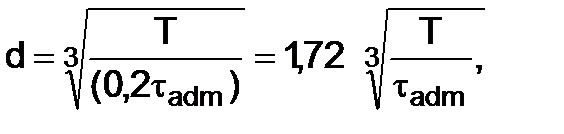 (4.13)
(4.13)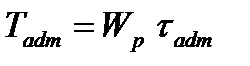 (4.14)
(4.14)


