Краткие теоретические сведения. Определение параметров схемы замещения катушки индуктивности осуществляется путём установления номинального режима при токе Iк = I2Н = 0,25 А
Определение параметров схемы замещения катушки индуктивности осуществляется путём установления номинального режима при токе Iк = I2Н = 0, 25 А, далее снимаются показания приборов: pW1 – ваттметр, измеряющий активную мощность, потребляемую катушкой индуктивности L2 Вт; pV2 – вольтметр, измеряющий напряжение на катушке индуктивности, В. R к = Р1/ I2H2, Z к = U2/ I2Н, где RK, ZL = ZK, XL = ХК – активное, полное, индуктивное сопротивления катушки L 2, Ом.

Рис. 2.1.2. Схема исследования электрической цепи с последовательным соединением катушки индуктивности, резистора и конденсатора
Величина ёмкости С2, при которой в электрической цепи (рис. 2.1.2) наступает резонанс напряжения, определяется исходя из условий резонанса напряжения:
где f – частота, Гц;
С2 – ёмкость конденсатора, Ф. При последовательном соединении резистивного, индуктивного и ёмкостного элементов составляется уравнение напряжения, согласно второму закону Кирхгофа в комплексной форме:
где
По закону Ома в комплексной форме определяется ток I, А:
где Пользуясь уравнением второго закона Кирхгофа, можно построить векторную диаграмму. Ток в электрической цепи есть величина постоянная, поэтому за основу построения векторной диаграммы принимаем ток. Векторы напряжений откладываются с учётом характера нагрузки. Вектор напряжения на резистивном элементе совпадает по фазе с вектором тока, на индуктивном элементе опережает на угол 90˚, на ёмкостном – отстаёт на угол 90˚. Приведём пример построения векторной диаграммы для условия, когда XL > XC (рис. 2.1.3),
Рис. 2.1.3. Векторная диаграмма при активно-индуктивно-ёмкостной нагрузке (XL > XC)
где φ – угол между вектором тока
Рис. 2.1.4. Треугольники: а) сопротивлений; б) мощностей; в) напряжений
Из треугольника сопротивлений (рис. 2.1.4, а):
Из треугольника мощностей (рис. 2.1.4, б):
P – активная мощность электрической цепи вычисляется по формуле
Q – реактивная мощность электрической цепи вычисляется по формуле
S – полная мощность электрической цепи. Когда индуктивное сопротивление XL становится равным ёмкостному сопротивлению XC (XC = XL, т.е.
Признаки резонанса напряжения следующие: 1. ток в цепи достигает наибольшего значения 2. 3. полная мощность электрической цепи равна активной, так как реактивная ёмкостная и реактивная индуктивная мощности равны между собой 4. сosφ становится равным единице(cosφ = 1).
|

 ,
, ,
,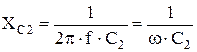 , Ом,
, Ом, – угловая частота, с-1;
– угловая частота, с-1; ,
, ,
,  ,
,  - комплексные напряжения на участках цепи;
- комплексные напряжения на участках цепи; – комплексный ток в цепи;
– комплексный ток в цепи; – полное комплексное сопротивление индуктивного элемента;
– полное комплексное сопротивление индуктивного элемента; – полное комплексное сопротивление ёмкостного элемента.
– полное комплексное сопротивление ёмкостного элемента. ,
, – полное комплексное сопротивление электрической цепи.
– полное комплексное сопротивление электрической цепи.
 – активная и реактивная составляющие напряжения;
– активная и реактивная составляющие напряжения; . Если XL > XC, то электрическая цепь имеет активно-индуктивный характер, то есть ток отстаёт по фазе от напряжения, если XL< XC, то цепь имеет активно-ёмкостный характер, то есть ток опережает напряжение по фазе. Действующее значение напряжения, приложенного к электрической цепи, можно определить из треугольника напряжений (рис. 2.1.4), полученного из векторной диаграммы
. Если XL > XC, то электрическая цепь имеет активно-индуктивный характер, то есть ток отстаёт по фазе от напряжения, если XL< XC, то цепь имеет активно-ёмкостный характер, то есть ток опережает напряжение по фазе. Действующее значение напряжения, приложенного к электрической цепи, можно определить из треугольника напряжений (рис. 2.1.4), полученного из векторной диаграммы а) б) в)
а) б) в) .
.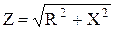 .
. , ВА.
, ВА. , Вт.
, Вт. , вар.
, вар. ), тогда в электрической неразветвлённой цепи наступает резонанс напряжений. Резонансом напряжений называют такой режим работы неразветвлённого участка цепи, который содержит индуктивный, ёмкостный и резистивный элементы последовательного контура и при котором ток и напряжение совпадают по фазе, то есть φ = 0:
), тогда в электрической неразветвлённой цепи наступает резонанс напряжений. Резонансом напряжений называют такой режим работы неразветвлённого участка цепи, который содержит индуктивный, ёмкостный и резистивный элементы последовательного контура и при котором ток и напряжение совпадают по фазе, то есть φ = 0: .
. , так как
, так как  ;
; ;
; ;
;


