Краткие теоретические сведения. Явление резонанса токов наблюдается в разветвленных цепях переменного тока, содержащих ветви цепи с индуктивностью и емкостью
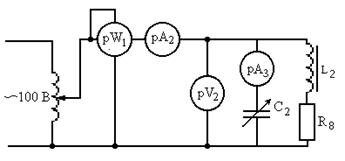
Явление резонанса токов наблюдается в разветвленных цепях переменного тока, содержащих ветви цепи с индуктивностью и емкостью. Суть резонанса заключается в том, что реактивная проводимость всей цепи равна нулю, то есть bL – bC = 0. Определение параметров нагрузки (рис.2.1.7) R8, XL2, ZК для цепи производится следующим образом: при расчёте сопротивления нагрузки (R8, XL2) необходимо зашунтировать катушку (L1, R22), установить номинальное напряжение (UН = 100 В) и снять показания приборов pW1, pV2, pA2, на основании показаний приборов вычислить:
где ω – угловая частота, с-1; f – промышленная частота, Гц; f = 50 Гц.
Коэффициент мощности cos φ рассчитывается следующим образом:
Согласно рис. 2.1.8 расчёт значения ёмкости C2 для повышения cos φ 1 до необходимого значения cos φ 2, производится так:
где P1 – активная мощность, потребляемая нагрузкой. Условие резонанса токов заключается в том, что bL = bC и значение ёмкости C2, при которой наступит резонанс токов, будет:
Токи в индуктивной катушке и в ёмкости при параллельном соединении определяются по 1 закону Кирхгофа в комплексной форме:
İ = İ K + İ C2= İ R8+ İ L2+ İ C2. Признаки резонансов токов: а) полная проводимость цепи активна и имеет наименьшее значение:
ток в неразветвлённой части цепи находится:
Рис. 2.1.7. Схема исследования катушки индуктивности
Рис. 2.1.8. Схема исследования однофазной цепи при параллельном соединении индуктивной катушки и конденсатора
б) ток в неразветвлённой части цепи чисто активный и минимальный
в) индуктивный и ёмкостные токи равны друг другу
г) коэффициент мощности cos φ при резонансе становится равным единице (cos φ = 1), векторная диаграмма при резонансе токов представлена на рис. 2.1.9.
Рис. 2.1.9. Векторная диаграмма при резонансе токов
|
, 
, 
, 
,
,
.
,
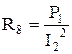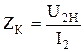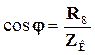, так как bC = ω С 2, следовательно 
, таким образом: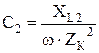 
, при этом 
= R2 8 + X2 L.
;
, 
,
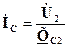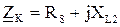или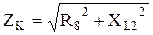 
.
;
;
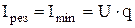