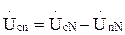Выводы по работе. 3. Электрические цепи трёхфазного переменного тока
3. Электрические цепи трёхфазного переменного тока Систему трех ЭДС, сдвинутых по фазе одна относительно другой, называют трехфазной. Если три ЭДС системы равны по амплитуде и сдвинуты по фазе одна относительно другой на угол 2π /3, то такую систему называют симметричной трехфазной системой. Совокупность устройств, по которым может протекать один из токов трехфазной системы ЭДС, называют фазой. Фазы принято обозначать А, В, С. Для трехфазной системы ЭДС можно записать: еA(t) + еB(t) + еC(t) = 0; Ė А +Ė В+Ė С = 0. При генерировании, передаче и преобразовании электрической энергии трехфазные цепи имеют ряд преимуществ по сравнению с однофазными: 1) меньший расход меди в проводах; 2) меньший расход стали в трансформаторах; 3) простота получения вращающегося поля в электродвигателях; 4) меньшая пульсация момента на валу роторов генераторов и двигателей. Таблица 3.1
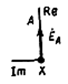
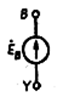
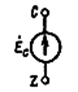
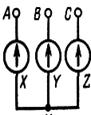
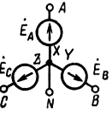
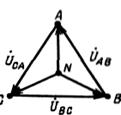
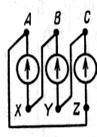
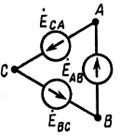
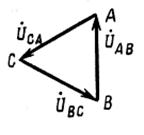
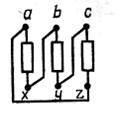
Мгновенные значения ЭДС трех фаз, их комплексные изображения, а также изображения на топографических диаграммах напряжений и схемах приведены в табл. 3.1. Здесь через А, В, С обозначены начала обмоток, а через X, Y, Z – их концы. Для источников и приемников трехфазных цепей существует две схемы соединений: 1) звездой ( При трехпроводной линии передачи источник и приемник могут быть соединены как треугольником, так и звездой. В последнем случае точка соединения концов обмоток (нейтраль) остается неподключенной, и схема не имеет нейтрального провода. По схеме соединения «звезда»: Ú Л = √ 3 Ú ф Ú AN = Ė A; Ú BN = Ė A (-1\2 – j√ 3/2); Ú CN = Ė A (-1\2 + j√ 3/2);
Ú AB = Ú AN –Ú BN = Ė A √ 3 (√ 3/2 + j /2); Ú BC = Ú BN – Ú CN = - jĖ A√ 3;
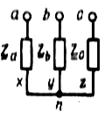
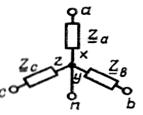
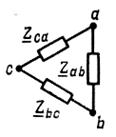
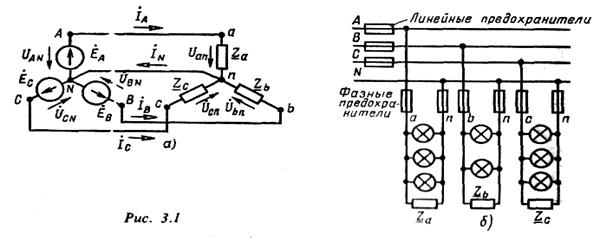
Ú CA = Ú CN – Ú AN = Ė A √ 3 (-√ 3/2 + j /2); По схеме соединения «треугольник»: Ú Л = Ú ф Ú AВ = EA; Ú BC = EB = EA (-1/2-j√ 3/2); Ú CA = EС = EA (-1/2+j√ 3/2); Четырехпроводную линию передачи применяют при соединении источника и приемника звездой. Один из проводов соединяет точки нейтралей, обозначаемые N для источника и n ─ для приемника. Схемы соединения источников и приемников, и топографические диаграммы напряжений источников приведены в табл. 3.2. Комплексные сопротивления различных фаз приемника при соединении звездой Z a, Z b, Z c, а при соединении треугольником – Z ab, Z bc и. Z ca. Источники и приемники соединяют с помощью проводов, подключаемых к точкам А к а, В к Ь, С и с в трехпроводной линии, а также N и n в четырехпроводной линии. Возможно переключение как источника, так и приемника с одной схемы на другую. При изменении вида соединения источника, например, со звезды на треугольник, напряжение между проводами линии (линейное напряжение) уменьшается в √ 3 раз. При аналогичном изменении вида соединения приемника, фазное напряжение приемника увеличивается в √ 3 раз. Переключая источник и приемник с соединения звездой на соединение треугольником и обратно, можно изменять фазное напряжение приемника в √ 3 и в 3 раза. Схема соединения источника и приемника звездой с нейтральным проводом показана на рис. 3.1а. Предполагается, что сопротивлениями проводов линии можно пренебречь. При симметричной схеме приемника, когда Za = Zb = Zc = Z; ток в нейтральном проводе, определяемый по первому закону Кирхгофа, равен нулю: İ N = İ A + İ B + İ C = (Ė A + Ė B + Ė C)/ z = 0. При несимметричной схеме приемника, когда Z a ≠ Z b ≠ Z c, ток в нейтральном проводе не равен нулю:
Примером несимметричного трехфазного приемника является
а) б) Рис. 3.1
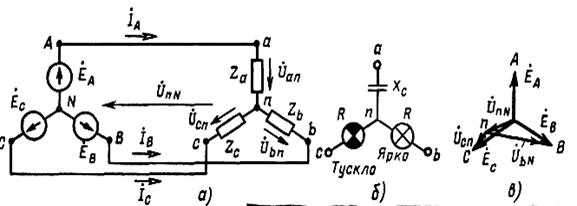
Линейные предохранители, в отличие от фазных, рассчитаны на большие токи. В нейтральном проводе N линейного предохранителя нет. Поскольку отключение нейтрали приводит к несимметричному распределению напряжений между однофазными приемниками и перегрузке некоторых из них в результате повышения напряжения. Векторные диаграммы токов для обоих случаев построены на рис. 3.2, в. Если поменять местами конденсатор и катушку (рис. 3.1), то схема соединения источника и приемника звездой без нейтрального провода будет (рис. 3.2, а). При симметричной нагрузке, когда Z a = Z b = Z c = Z, напряжение между нейтральной точкой источника N и нейтральной точкой приемника n равно нулю, так как по формуле двух узлов.
и наличие или отсутствие нейтрального провода не изменяет токов в фазах приемника. При несимметричной нагрузке, когда Z a ≠ Z b ≠ Z c, напряжение
Рис. 3.2
Эти напряжения по модулю могут отличаться одно от другого и меняться с изменением сопротивлений других фаз. Поэтому рассматриваемую схему применяют только для приемников с симметричной нагрузкой. В отдельных случаях ее могут использовать для получения несимметричных систем напряжений трех фаз.
|
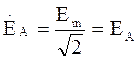
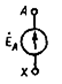
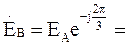
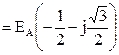
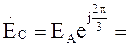
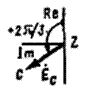
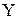), 2) треугольником (
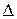). В первом случае, все концы (X, Y, Z) обмоток источников соединяются между собой, а к началам фаз (А, B, С) подводится питание. От источника к приемнику ведут четыре провода: три подсоединены к началам трех обмоток (А, В, С), четвертый N – к соединённым между собой концам обмоток. Во втором случае, к концу каждой обмотки подсоединяют начало следующей обмотки. При этом образуется замкнутый контур, состоящий из трех источников ЭДС с различными фазами. Так как сумма ЭДС фаз равна нулю, то ток в этом контуре отсутствует. Соединение источника и приемника производят с помощью трех или четырех проводов. При этом образуется трёхпроводная или четырёхпроводная линия передачи электрической энергии от источника к приемнику.
; 
; 
,
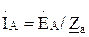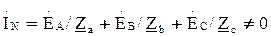
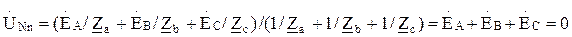
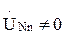. Определив по формуле двух узлов UnN, можно найти напряжение на каждой фазе приемника:
; 
; 
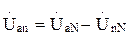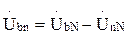