Методика проведения опытов. При выполнении данной работы исследуется форма напряжения при наличии LC-фильтра и без него (при анализе форм напряжения следует использовать осциллограф)
При выполнении данной работы исследуется форма напряжения при наличии LC-фильтра и без него (при анализе форм напряжения следует использовать осциллограф). Параметры LC-фильтра рассчитываются из условия резонанса напряжения на одной из гармоник. По результатам измерений производится запись напряжения источника в виде ряда Фурье. Действующее значение несинусоидальных напряжений и токов будут определяться:
где U1, U2, …Un; I1, I2, …In; - соответственно действующие значения отдельных гармоник напряжения и тока.
где U1m, U2m, …Unm; I1m, I2m, …Inm; – соответственно амплитудные значения гармонических составляющих напряжения и тока. В лабораторной работе с помощью резистора R1 устанавливается заданный угол отпирания тиристора. Номинал R1 рассчитывается по известным параметрам угла открывания тиристора и емкости конденсатора c1 = 2, 2 мкФ.
Из формулы определяется значение R1 для получения заданного преподавателем угла
Численные значения отдельных гармонических составляющих в долях от амплитудного значения напряжения и их начальные фазы представлены в табл. 2.1.7. Таблица 2.1.7
В качестве нагрузки в данной лабораторной работе используется цепь со смешанным сопротивлением (рис. 2.1.21)
Рис. 2.1.21
Величина емкости С2 выбирается из достижения требуемого режима работы цепи. Данную цепь для расчета постоянной составляющей и гармонических составляющих ряда Фурье для несинусоидального тока можно представить в виде схем замещения:
1. Рис. 2.1.22 – для расчета постоянной составляющей тока:
R3 = 150 Ом
I0=U0/R3 Рис. 2.1.22
2. Рис. 2.1.23 – для расчета 1-й гармонической составляющей тока:
Рис. 2.1.23
3. Рис. 2.1.24 – для расчета 2-й гармонической составляющей тока:
Рис. 2.1.24 Действующее значение тока определяется:
Значение емкости C2, при котором наступает резонанс напряжений в цепи, можно найти из условия резонанса напряжения (рис. 2.1.25)
Рис. 2.1.25 Следовательно: Рис. 2.1.25 где ω – угловая частота, с-1.
Программа работы 1. Изучить схему управляемого выпрямителя на стенде. 2. Установит одно из значений угла управления тиристорами. 3. Отключить исследуемую цепь и, измерив среднее значение напряжения источника, определить его амплитудное значение. 4. Записать напряжение источника в виде ряда Фурье. 5. Рассчитать значение С2 для фильтрации высших гармонических составляющих и для резонанса напряжений и определить величину I0 и Iрез по методу положения (суперпозиции). 6. Установить на стенде значения С2 для фильтрации высших гармоник и для резонанса напряжения, измерить величину I0 и Iрез и сравнить их с результатом расчета. Данные свести в таблицу 2.1.8. Таблица 2.1.8
Контрольные вопросы 1. Изложите основные положения, на которых основывается методика расчета линейных цепей при периодических несинусоидальных токах. 2. Как определяются коэффициенты ряда Фурье? 3. Как определяются амплитуды и фазы высших гармоник аналитическим способом? 4. Охарактеризуйте физический смысл действующего значения тока (напряжения) несинусоидального тока. 5. Как определяются активная и полная мощности несинусоидального тока? 6. Как можно изменить несинусоидальные токи и напряжения?
|

 ,
, 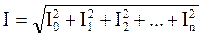 ,
, ,
,  – постоянные составляющие несинусоидального напряжения и тока, разложенных в ряд Фурье.
– постоянные составляющие несинусоидального напряжения и тока, разложенных в ряд Фурье.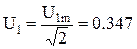 ;
; 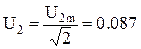 ;
;  ;
; ;
; 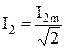 ;
;  .
. .
. отпирания тиристора. Гармонический состав напряжения управляемого выпрямителя определяется рядом Фурье:
отпирания тиристора. Гармонический состав напряжения управляемого выпрямителя определяется рядом Фурье: .
.



 ;
; ;
; ;
;


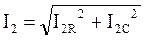
 .
.

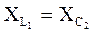 ;
;

 .
. с-1.
с-1.


