Электрические цепи однофазного переменного тока
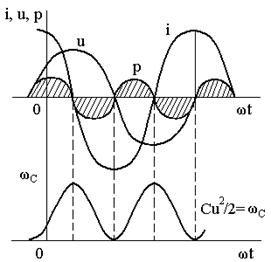
Ток, изменяющийся во времени по синусоидальному закону, называется переменным синусоидальным током. i(t) = Imsin(ω t + ψ i) = Imcos(ω t + ψ i + π /2), (2.1) где i(t) – мгновенное (зависящее от времени) значение тока (рис. 2.1); Im – амплитуда тока; ω – угловая частота тока; ψ i – начальная фаза тока.
Рис. 2.1
Среднее значение тока
Среднеквадратичное значение тока
В качестве действующего значения синусоидального тока и напряжения принимается его среднеквадратичное значение:
где Im, Um– амплитудное (максимальное) значение тока и напряжения. Период синусоидального тока T = 2π /ω. Синусоидальная функция времени i(t) может быть получена, как проекция на вертикальную ось комплексной плоскости вектора Вектор İ где Комплексная амплитуда тока в алгебраической форме
где Комплексная амплитуда тока в показательной форме
где Вращение комплексной амплитуды с угловой частотой ω аналитически выражают следующим образом:
Мгновенное значение тока i(t)
где ω – угловая частота, ψ i – начальная фаза. Большой буквой с точкой наверху обозначают только комплексные изображения синусоидальных функций времени. Математическое описание синусоидальной функции дано на примере тока i(t). Аналогично описывают математически ЭДС е(t), напряжение u(t) и потокосцепление Ψ (t). Пассивными линейными элементами (приемниками) электрической цепи синусоидального тока являются: резистивный элемент (резистор), обладающий сопротивлением R; индуктивный элемент (индуктивная катушка) с индуктивностью L; и емкостный элемент (конденсатор) с емкостью С. Сопротивление, индуктивность и емкость являются коэффициентами пропорциональности в выражениях для напряжения u, потокосцепления Ψ и количества электричества qв линейных цепях через ток и напряжение: u = Ri; Ψ = Li; q = С u.(2.6)
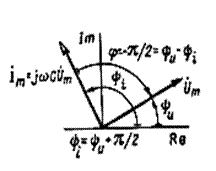
Индуктивный элемент рассматривают, как зависимый источник напряжения, ЭДС которого представляется как источник. При этом положительные направления для ЭДС и тока принимаются совпадающими согласно закону электромагнитной индукции е = – dΨ /dt или е = dΨ /dt, если индуктивный элемент рассматривается, как приемник, и положительное направление ЭДС принимается противоположным условно-положительному направлению, выбранному для тока. В обоих случаях напряжение на зажимах индуктивного элемента
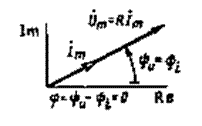
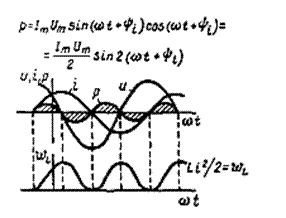
Мгновенные значения напряжения u, тока i и мощности р для трех элементов цепи синусоидального тока приведены в табл. 2.1. Там же даны комплексные изображения синусоидальных величин Под комплексными изображениями синусоидальных функций вре-мени понимают комплексные действующие значения Под WL понимается энергия магнитного поля, а под WC - энергия электрического поля. Рассмотрение синусоидальных токов и напряжений в резистивном, индуктивном и емкостном элементах (табл. 2.1) для линейных цепей синусоидального тока позволяет обобщить законы Ома и Кирхгофа и представить их в форме (табл. 2.2), где Zt = Rk + jXk– комплексное сопротивление ветви k; Zк= | Zk | = √ (Rк2 + Xк2)–модуль комплексного сопротивления или полное сопротивление; arc tg (Xk/Rk)= φ к –аргумент комплексного сопротивления ветви k или угол, на который ток iк отстает от напряжения uk. Если ветвь состоит только из резистивного элемента с сопротивле-нием Rk, то φ k = 0; если ветвь содержит только индуктивный элемент Lk, то φ k = π /2; а если только емкостный элемент Ck, то φ k = -π /2.
Таблица 2.1
Продолжение таблицы 2.1 Таблица 2.2
|



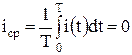 (2.2)
(2.2) (2.3)
(2.3) I = iср.кв. =
I = iср.кв. =  ; U = uср.кв.=
; U = uср.кв.= 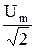 ,
,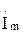 (рис. 2.1), вращающегося в положительном направлении стрелки с угловой частотой ω. Вектор
(рис. 2.1), вращающегося в положительном направлении стрелки с угловой частотой ω. Вектор 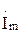 на комплексной плоскости выражают комплексным числом и называют комплексной амплитудой тока.
на комплексной плоскости выражают комплексным числом и называют комплексной амплитудой тока. ,
, – мнимая единица или единичный вектор с углом поворота на 90 градусов.
– мнимая единица или единичный вектор с углом поворота на 90 градусов. ,
,
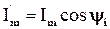 ;
; 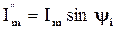 ;
; 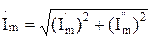 .
.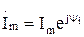 ,
, .
. . (2.4)
. (2.4) , (2.5)
, (2.5)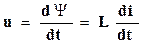 .
.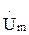 и
и 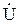 ,
,  и
и 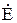 . Комп-лексные сопротивления Z и проводимость Y представляют собой опе-раторы, преобразующие синусоидальный ток i(t) в синусоидальное напряжение u (t) и наоборот.
. Комп-лексные сопротивления Z и проводимость Y представляют собой опе-раторы, преобразующие синусоидальный ток i(t) в синусоидальное напряжение u (t) и наоборот.
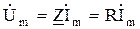 или
или  ;
;  ,
где R – активное сопротивление; G – активная проводимость
,
где R – активное сопротивление; G – активная проводимость
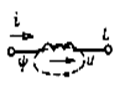
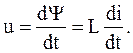 где L – коэффициент пропорциональности между потокосцеплением и током i
где L – коэффициент пропорциональности между потокосцеплением и током i
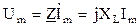 или
или 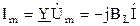 ;
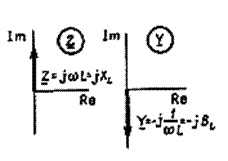
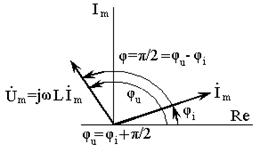
Z = 1/У =jω L=jXL
где XL = ω L – реактивное (индуктивное)
сопротивление;
BL = 1/XL = 1/(ω L) – реактивная (индуктивная) проводимость
;
Z = 1/У =jω L=jXL
где XL = ω L – реактивное (индуктивное)
сопротивление;
BL = 1/XL = 1/(ω L) – реактивная (индуктивная) проводимость

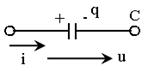
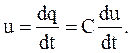 где С – коэффициент пропорциональности между зарядом q и напряжением u
где С – коэффициент пропорциональности между зарядом q и напряжением u
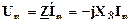 ;
; 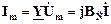 ;
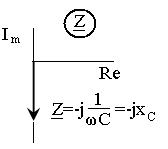
У = 1/Z =jω C=jBC
где XС=1/BС=1/(ω С) – реактивное (емкостное) сопротивление
BC=ω C – реактивная (емкостная) проводимость
;
У = 1/Z =jω C=jBC
где XС=1/BС=1/(ω С) – реактивное (емкостное) сопротивление
BC=ω C – реактивная (емкостная) проводимость