Переходные процессы

 

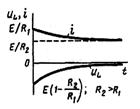
Процесс в электрической цепи, при переходе от одного установившегося режима к другому, называют переходным. В электрических цепях, содержащих реактивные элементы, накапливающие электрическую или магнитную энергию, переходные процессы возникают при: а) замыкании или размыкании какого-либо участка цепи; б) изменении напряжений или токов источников.

Анализ переходных процессов в цепях производят на интервале времени 0 < t < ∞. Любые переключения в электрической цепи называют коммутацией. Моментом коммутации обычно считают t = 0. В момент коммутации, энергия, запасенная в индуктивном Li²/2 или емкостном Сu²/2 элементах, не может изменяться скачком, и, следовательно, ток в индуктивном элементе и напряжение на емкостном элементе также не могут изменяться скачком (законы коммутации ). Для расчета переходных процессов применяют три метода: 1) классический, 2) операторный, 3) частотный. В настоящем пособии рассматривается только классический метод расчета.

Для переходных процессов законы Ома и Кирхгофа, записанные для мгновенных значений, справедливы, но для тока в индуктивном и напряжения на емкостном элементах необходимо учитывать начальные условия i_L(0) и u_с(0):

i_L = i_L(0) + (1/L) ∫ u_Ldt (6.1)

u_C = u_C(0) + (1/C) ∫ i_Cdt

Система дифференциальных уравнений, составленная по первому и второму законам Кирхгофа, может быть сведена к одному уравнению для любого из токов или напряжений в цепи:

dⁿ_i/dtⁿ + a₁d^n-1i/dtⁿ +…+ a_n-1di/dt + a_ni = f_i(t)

dⁿu/dtⁿ + b₁d^n-1u/dtⁿ +…+ b_n-1du/dt + a_nu = f_u(t) (6.2)

где a_i = b_i – постоянные коэффициенты, зависящие от параметров (R, L и С) цепи;

f_t(t)…f_tut) – функции времени, зависящие от ЭДС и токов источников.

Решение неоднородного дифференциального уравнения (6.2) классическим методом разбивается на две части: 1) частное решение – принужденная составляющая i_np(t) уравнения (6.2), зависящая от его правой части; 2) общее решение – свободная составляющая i_CB(t) однородного уравнения, зависящая от левой его части:

i_св = A₁е ^p₁^t + A₂е ^р₂^t+... + A_n е ^p_n^t, (6.3)

где А₁, А₂,...А_n–постоянные интегрирования, определенные из начальных условий на основании законов коммутации; р₁, р₂, _….р_n - корни характеристического уравнения

рⁿ + a₁ p^n-1 + а₂ р^n-2 +... + a_n = 0.(6.4)

При отсутствии источников с апериодически изменяющимся напряжением, принужденную составляющую i_np определяют, как установившееся значение тока i_уст при t → ∞.

Если среди корней характеристического уравнения имеется пара комплексно-сопряженных корней, например р_{1, 2}= –β ±jω ₁, то

A₁е ^p₁^t + A₂е ^р₂^t = Aе^{- -β t} sin (ω ₁t + γ), (6.5)

где А, γ – находят из начальных условий.

Значения переходных токов и напряжений на индуктивном элементе при переключениях в RL-цепях, при постоянной ЭДС (е = Е) и

синусоидальной [е = Е_msin(ω t +ψ _е) ], приведены в табл. 6.1. Для постоянной ЭДС показаны графики i(t) и U_L(t). Чтобы избежать перенапряжений в цепи переключение производят без ее разрыва с индуктивным элементом

(переключатель 1→ 2). Дифференциальное уравнение первого порядка и характеристическое уравнение имеет один корень P₁. При ω L > > R (то есть φ ≈ π /2), и подключении источника синусоидальной ЭДС (при ψ _с = 0) ток в момент времени t_l = π /ω достигает в два раза большего значения, чем установившееся E_м/Z. В этом случае [sin(π – π /2) – sin(– π /2)]= 2,

е ^р₁^t₁ ≈ 1. Поскольку подключение источника происходит в случайный момент времени 0 < ψ _е < 2π, то, в зависимости от момента включения, максимальное значение переходного тока в цепи с индуктивным элементом может находиться в пределах от E_m/Z до 2E_m/Z.

Таблица 6.1

Схема переключения	Ток и напряжение индуктивного элемента при t> 0	Корни характеристического уравнения
е = Е	е = Еmsin(ω t + Ψ e)
	I=E/R(1-ep 1t); UL=Eep 1t	i= Em/Z[sin(ω t + ψ е-φ)- sin(ψ е- φ)е р 1t]; uL= E/Z[wLcos(wt+ψ e-φ)+ +Rsin(ψ е-φ)ep 1t]; Z = √ R2 + (ω L)2; φ = arctg(ω L/R)	P1=-R/L
	I=E/R(ep 1t) UL=-E(1+R2/R1)ep 1t	i = Em/Z [sin (ψ еe - φ) ep 1t ]; uL = -(R1+R2) Em/Z1 sin (ψ е – -ψ 1) ep 1t ]; Z = √ R2 + (ω L)2; φ = arctg(ω L/R)	P1=-
	ep 1t uL=E(1-R2/R1) ep 1t	i= Em/Z [sin (ω t + ψ e – φ)+ +Em[sin(ψ e-φ 1)/Z1- -sin(ψ e-φ 2)/Z2] ep 1t; uL = Em {(wL/Z2) cos (wt + ψ e – φ 2) -R2(sin (ψ е – φ 1)/Z1- sin (ψ е– φ 2)/Z2] ep 1t }; Z1 = √ R21 + (ω L)2; Z2 = √ R22 + (ω L)2 φ 1 = arctg (ω L/R1); φ 2 = arctg (ω L/R2)	P1= - R2/L

Таблица 6.2

Схема переключения	Ток и напряжение емкостного элемента при t > 0	Корни хар-кого уравнения
е=Е	е = Еmsin(ω t + Ψ e)
	i=(E/R) ep 1t; uс=E(1- ep1t)	i= Em/Z [sin (ω t + ψ e – φ)-cos(ψ e- -φ)/(ω RC) ep 1t ]; uC = E/ω CZ[-cos (ω t + ψ e – φ)+ +cos (ψ е – φ) ep 1t ]; Z = √ R2 + (1/ω C)2; φ = -arctg (1/ω RC)	P1= -1/RC
	i=-(E/R) ep 1t; uC = E ep 1t	i= Em/Zω RC [cos (ψ e - φ) ep 1t]; u c = Em/Zω C cos (ψ e – φ) ep 1t ]; Z = √ R2 + (1/ω C)2; φ = -arctg (1/ω RC)	P1= -1/RC
	i=(E/R) ep 1t; uс = Eep 1t	i= Em/R (sin ψ е) ep 1t; uс = Em (sinψ е) ep 1t.	P1= -1/RC