Редактор М.Е. Цветкова. [1] Глава 9 подготовлена доцентом кафедры информационных технологий, математики и средств дистанционн
Редактор М.Е. Цветкова Корректор Н.А. Орлова Лицензия № 020446 от 04.03.97. Подписано в печать 22.04.02. Формат бумаги 60´ 84 1/16. Бумага газетная. Печать трафаретная. Усл. печ. л. 3, 75. Уч.-изд.л. 3, 75. Тираж 25 экз. Заказ 093 Ц. 50 р. Рязанская государственная радиотехническая академия. 391000, Рязань, ул. Гагарина, 59/1. Редакционно-издательский центр РГРТА.
ISBN 5-7722-0190-5 Ó Рязанская государственная радиотехническая академия, 2002  =4, так как =4, так как   ( (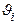 )=0.9= = )=0.9= =  ( (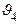 ). Последнее в (10.9) дает ). Последнее в (10.9) дает  =0 (значению =0 (значению  =0 в табл. 10.6 соответствует КАЧЕСТВО2= неустранимый дефект). По (10.11) и табл.10.6 определяем =0 в табл. 10.6 соответствует КАЧЕСТВО2= неустранимый дефект). По (10.11) и табл.10.6 определяем  = неустранимый дефект = 1/0+0.5/1+0/2. Композируя = неустранимый дефект = 1/0+0.5/1+0/2. Композируя  с матрицей с матрицей  ( (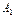 ( ( ) ) 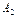 ( (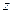 )) (табл. 10.8), по аналогии с )) (табл. 10.8), по аналогии с 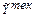 получаем получаем  =1/0+0.5/1+0/2, что дает =1/0+0.5/1+0/2, что дает 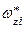 =0, так как =0, так как   ( ( )=1= )=1=  ( ( ). Параметр ). Параметр 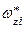 =0, соответствующий =0, соответствующий  =0 таблицы 10.7, определяет переменную УГОЛ= малый. По (10.16) находим =0 таблицы 10.7, определяет переменную УГОЛ= малый. По (10.16) находим 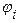 =900. =900.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК 1. Обработка нечеткой информации в системах принятия решения / А.Н. Борисов, А.В. Алексеев и др. М.: Радио и связь, 1989. 304 с. 2. Левин Р., Дранг Д., Эделсон Б. Практическое введение в технологию искусственного интеллекта и экспертных систем с иллюстрациями на Бейсике. Пер. с англ. / Предисловие М.Л. Сальникова, Ю.В. Сальниковой. М.: Финансы и статистика, 1991. 239 с. 3. Алиев Р.А. Интеллектуальные роботы с нечеткими базами знаний. М.: Радио и связь, 1994. 177 с. 4. Марселус Д. Программирование экспертных систем на ТУРБО- ПРОЛОГЕ. М.: Финансы и статистика, 1994. 256 с. 5. Герман О.В. Введение в теорию экспертных систем и обработку знаний. Мн.: ДизайнПРО, 1995. 255 с. 6. Статические и динамические экспертные системы: Учеб. пособие / Э.В. Попов, И.Б. Фоминых, Е.Б. Кисель, М.Д. Шапот. М.: Финансы и статистика, 1996. 320 с. 7. Змитрович А.И. Интеллектуальные информационные системы. – Мн.: НТООО Тетра-систем, 1997. 368 с. 8. Гаврилова Т.А., Хорошевский В.Ф. Базы знаний интеллектуальных систем. СПб.: Питер, 2000. 384 с. 9. Корнеев В.В. и др. Базы данных. Интеллектуальная обработка информации. М.: Нолидж, 2000. 352 с. 10. Хомоненко А.Д., Цыганков В.М., Мальцев М.Г. Базы данных: Учебник для высших учебных заведений / Под ред. проф. А.Д. Хомоненко. СПб.: КОРОНА принт, 2000. 416 с.
Чтобы придать формуле содержание, ее интерпретируют как утверждение, распространяющееся на некоторую область
Формула называется теоремой, если существует доказательство, в котором она является последней.
|


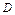 (область интерпретации).
(область интерпретации). Наиболее распространенной формальной системой является исчисление предикатов первого порядка. Основной задачей при получении новых знаний в рамках исчисления предикатов является выяснение истинности или ложности заданной формулы на области
Наиболее распространенной формальной системой является исчисление предикатов первого порядка. Основной задачей при получении новых знаний в рамках исчисления предикатов является выяснение истинности или ложности заданной формулы на области 


