Принцип резолюций
Принцип резолюций позволяет из двух предикатных предложений получить третье, что соответствует процедуре логического вывода новых предложений из множества исходных. Пусть имеются два конкретных предложения: Достоинствами формально-логической модели представления знаний являются единственность теоретического обоснования и возможность реализации системы формально точных определений и выводов. Недостатком формально-логической модели являются жесткие ограничения, свойственные всем формальным моделям.
Если с точки зрения технологии параметры Для уяснения связи
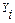 дает дает 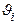 , определяющее лингвистическую переменную “КАЧЕСТВО1”, а (10.7) по всем табличным , определяющее лингвистическую переменную “КАЧЕСТВО1”, а (10.7) по всем табличным
предикатов. Прямая дедукция: если Пример задачи по методу “от фактов к цели”. Факт 1: Иванов – преподаватель математического факультета (формализованная запись - преп.(матем., иванов)). Факт 2: Петрова – студентка факультетаинформатики (студ.(информ., петрова)). Правило 1: если Цель 1 (запрос): Может ли Иванов быть экзаменатором у Петровой (экзам.(иванов, петрова))? Утвердительный ответ на поставленный вопрос имеет вид следующей теоремы: (факт1 Ù факт2 Ù правило1) ® цель1. Доказательство теоремы сводится к доказательству истинности данного логического выражения. С помощью табл. 1.1 перепишем теорему как Ø (факт1 Ù факт2 Ù правило1) Ú цель1. Истинность этого выражения соответствует ложности следующего выражения: 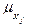 , принимающей значения в интервале [0, 1] для всех , принимающей значения в интервале [0, 1] для всех 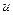 из универсумов из универсумов 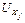 = {0, 1, …, 10} (записывается как = {0, 1, …, 10} (записывается как 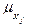 : : 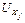 ®[0, 1]). Значения переменной “ПАРАМЕТР” приведены в табл. 10.3. ®[0, 1]). Значения переменной “ПАРАМЕТР” приведены в табл. 10.3.
Таблица 10.3. Значения переменной " ПАРАМЕТР"
Так как
где Ранее было
Для вычисления синглтонов
-
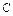 1Ù 1Ù 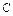 2. Докажем предыдущую теорему методом обратной дедукции. Для этого преобразуем с учетом табл. 1.1 ранее используемую формулу Ø (факт1 Ù факт2 Ù правило1) Ú цель1: 2. Докажем предыдущую теорему методом обратной дедукции. Для этого преобразуем с учетом табл. 1.1 ранее используемую формулу Ø (факт1 Ù факт2 Ù правило1) Ú цель1:
Ø факт1 Ú Ø факт2 Ú Ø правило1 Ú цель1. Последнее полностью соответствует теореме обратной дедукции. Вначале используем принцип резолюций. Этап 1. Преобразуем часть Ø правило1 к виду преп.( и подставим еев последнюю формулу теоремы: Ø факт1 Ú Ø факт2 Ú (преп.( Ù Ø равно( С учетом двойственности правила согласия правилу резолюций из цели 1 и отрицания правила 1 выводим новую цель 2: преп.( где осуществлена замена переменных на известные константы цели 1. Этап 2. Из цели 2 и отрицания факта 1 выводим цель 3: студ.( Этап 3. Из цели 3 и отрицания факта 2 находим факт 3: Ø равно(матем., информ.). Получили известный (неиндексированный) факт и факт истинный. Теорема доказана. Если следовать только правилам эквивалентных формул, то на первом этапе доказательства теоремы дизъюнкция Ø правило1 Ú цель1 дает предложение цель2 Ú цель1, на втором этапе имеем Ø факт1 Ú цель2=цель3 Ú цель2, на третьем этапе получаем Ø факт2 Ú цель3=факт3 Ú цель3. В итоге вместо Ø факт1 Ú Ø факт2 Ú Ú Ø правило1 Ú цель1 оказывается факт3 Ú цель3 Ú цель2 Ú цель1=И (истинно), так как факт3=И. Теорема доказана. Типичными представителями продукционной модели с прямым выводом знаний являются диагностические системы, а моделей с обратным поиском решения – системы проектирования.
|

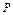 1Ú
1Ú  и Ø
и Ø  2Ú
2Ú 
 (
(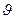 ))Ù [(1-
))Ù [(1- 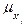 (
( (
(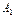 (
(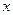 )
) 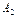 (
(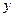 )) выражение
)) выражение
 1-
1-  (
(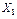 ,
, 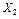 неравнозначны, например при определении качества изделий большее значение имеет кривизна, чем температура, то в последнем выражении вместо
неравнозначны, например при определении качества изделий большее значение имеет кривизна, чем температура, то в последнем выражении вместо 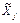 и функций принадлежности
и функций принадлежности  (
(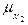 (
(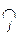
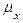 (
(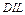 ) нечетких множеств, необходимо представить входное нечеткое множество как
) нечетких множеств, необходимо представить входное нечеткое множество как 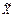 =
=  Ç
Ç 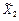 ) и, соответственно,
) и, соответственно, 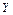 используем экспертное правило: “Если
используем экспертное правило: “Если 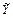 наивысшее иначе
наивысшее иначе  ,
, 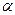 =1:
=1: [(
[( (
( )-1)
)-1)  ], (10.6)
], (10.6) ê
ê 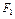 ,
, 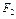 , …,
, …,  ,
,  - логические выражения, то
- логические выражения, то  и
и 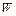 - студентка факультета
- студентка факультета 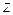 при
при 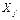 - промышленный параметр, а
- промышленный параметр, а  ], (10.1)
], (10.1) (
( )/
)/ 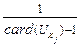 ê
ê 


