Предикатом или логической функцией называется функция от любого количества ( ) аргументов, принимающая значения 1 (истина) и 0 (ложь) (
) аргументов, принимающая значения 1 (истина) и 0 (ложь) ( -местный предикат).
-местный предикат).
Алфавит языка предикатов первого порядка:
- разделители: запятая - “, ”, открывающая скобка - “(”, закрывающая скобка - “)”;
- константы – строчные буквы – “ 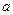 ”, …;
”, …;
- переменные – прописные (заглавные) буквы – “  ”, …;
”, …;
- предикаты – заглавные буквы;
- функции (не предикаты) – строчные буквы – “  ”, …;
”, …;
- логические операции:
1) Ø - отрицание,
2) Ù - коньюнкция,
3) Ú - дизъюнкция,
4) ® - импликация (если…то…),
5) «- эквивалентность (…тогда и только тогда, когда…),
6) $ - квантор существования (сушествует…),
7) " - квантор общности (для любого…).
Выражение “первого порядка” связано с формулами, в которых запрещается квантифицировать символы предикатов и функций.
Формулой алгебры логики (пропозициональной формой) называют всякое высказывание, составленное из некоторых исходных высказываний посредством логических операций.
Терм – выражение, включающее константы, переменные и n -местные функции от термов.
Атом – элементарная функция – это выражение, включающее константы, переменные, функции и предикаты.
Правильная формула (ПФ) – это атом, Ø  ,
,  Ú
Ú  ,
,  Ù
Ù  , ($
, ($  )
)  , ("
, ("  )
)  , где
, где  ,
,  – ПФ;
– ПФ;  – переменная; ($
– переменная; ($  )
)  означает: существует
означает: существует  , для которогот справедливо
, для которогот справедливо  ; ("
; ("  )
)  означает: для любого
означает: для любого  справедливо
справедливо  .
.
Правило вывода – процедура, которая из одной или нескольких ПФ
дефект =1/0+0.5/1+0/2,  =малый = 1/0+0.5/1+0/2.
=малый = 1/0+0.5/1+0/2.
Для получения нечеткого множества, соответствующего текущему углу поворота манипулятора как логического следствия, в качестве нечеткого бинарного отношения воспользуемся выражением
 (
(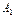 (
( )
) 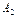 (
(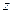 ))=(
))=( ´
´ 
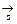
 ´
´  )Ç (Ø
)Ç (Ø  ´
´ 
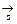
 ´ Ø
´ Ø  ),
),
где 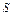 обозначает
обозначает 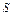 -логику. Или
-логику. Или  (
(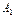 (
( )
) 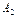 (
(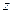 )) =
)) =  (
( )
) 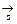
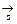
 (
( ))Ù ((1-(
))Ù ((1-(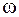 ))
)) 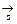 (1-
(1-  (
( )) ] /(
)) ] /( ,
,  ). По аналогии с (10.5)
). По аналогии с (10.5)
 1, если
1, если  (
( )=
)=  (
( ),
),
 (
( ,
,  ) = (10.14) 0, если
) = (10.14) 0, если  (
( )¹
)¹  (
( ).
).
Согласно этой формуле и (10.10), (10.12) строим матрицу отношений  (
(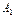 (
( )
) 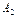 (
(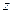 )) - табл. 10.8. На основе табл. 10.8 рассчитываем
)) - табл. 10.8. На основе табл. 10.8 рассчитываем
Таблица 10.8. Матрица отношений  (
(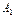 (
( )
) 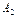 (
(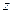 ))
))
нечеткое множество  , определяющее угол поворота, в соответствии с текущим
, определяющее угол поворота, в соответствии с текущим  =
=  по аналогии с
по аналогии с  - (10.8):
- (10.8):
 =
= 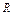 (
(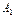 (
( ))o
))o  (
(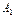 (
( ),
), 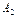 (
(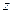 ))=
))=  o
o  (
(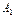 (
( )
) 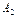 (
(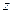 )). (10.15)
)). (10.15)
Так как конкретное значение угла поворота 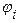 связано с параметром
связано с параметром 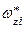 ,
,
задаем 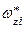 Î
Î  ½
½  (
(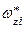 )=
)= 
 (
( ),
),  =
= 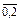 . Подставляя
. Подставляя 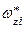 в выражение
в выражение
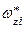 =
=  [(
[( (
( )-1)
)-1)  ] ê, (10.16)
] ê, (10.16)
находим
Таблица 1.1. Эквивалентные ПФ
| Исходная ПФ
| Эквивалентная ПФ
| Вид закона
|
Ø  (Ø (Ø  ) )
| 
|
|
 ® ® 
| Ø  Ú Ú 
|
|
 « «
| ( ® ®  )Ù ( )Ù ( ® ®  ) )
|
|
Ø ( Ù Ù  ) )
| Ø  Ú Ø Ú Ø 
| Закон де Моргана
|
Ø ( Ú Ú  ) )
| Ø  Ù Ø Ù Ø 
| Закон де Моргана
|
 Ù ( Ù ( Ú Ú  ) )
| ( Ù Ù  )Ú ( )Ú ( Ù Ù  ) )
| Закон дистрибутивности
|
 Ú ( Ú ( Ù Ù  ) )
| ( Ú Ú  )Ù ( )Ù ( Ú Ú  ) )
| Закон дистрибутивности
|
 Ú Ú 
|  Ú Ú 
| Закон коммутативности
|
 Ù Ù 
|  Ù Ù 
| Закон коммутативности
|
( Ú Ú  )Ú )Ú 
|  Ú ( Ú ( Ú Ú  ) )
| Закон ассоциативности
|
( Ù Ù  )Ù )Ù 
|  Ù ( Ù ( Ù Ù  ) )
| Закон ассоциативности
|
 ® ® 
| Ø  ® Ø ® Ø 
| Контрапозиционный закон
|
 Ù Ø Ù Ø 
|
|
|
 Ú Ø Ú Ø 
|
|
|
 Ù 0 Ù 0
|
|
|
 Ù 1 Ù 1
| 
|
|
 Ú 0 Ú 0
| 
|
|
 Ú 1 Ú 1
|
|
|
Ø ($   ( ( )) ))
| "  (Ø (Ø  ( ( )) ))
|
|
Ø ("   ( ( )) ))
| $  (Ø (Ø  ( ( )) ))
|
|
"  ( ( ( ( )Ù )Ù  ( ( )) ))
| "   ( ( )Ù " )Ù "   ( ( ) )
|
|
$  ( ( ( ( )Ú )Ú  ( ( )) ))
| $   ( ( )Ú $ )Ú $   ( ( ) )
|
|
"   ( ( ) )
| " 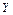  ( (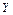 ) )
| Закон немых переменных
|
$   ( ( ) )
| $ 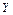  ( (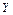 ) )
| Закон немых переменных
|
Ú Ø  (
( ,
, 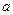 )Ú
)Ú 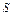 (
(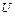 )Ú Ø
)Ú Ø 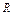 (
(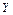 ,
, 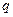 (
( ,
, 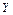 ))Ú
))Ú 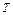 (
( ,
, 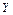 ))).
))).
Если учесть, что все переменные в ПФ связаны, то кванторы общности относятся ко всей матрице и их можно опустить. Остается матрица. В ней коньюнкции ПФ можно заменить на множество ПФ (по числу символов коньюнкции плюс единица). Пример для последней формулы:
……………………………………………………………………………………
91. 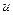 =
=  =9,
=9, 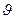 =
= 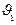 =1;
=1; 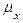 (
( ) =0.1,
) =0.1,  (
(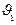 ) = 0.1;
) = 0.1; 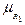 (
( ,
, 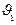 ) = =
) = =  (
(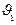 ) =1;
) =1;
101. 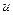 =
= 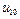 =10,
=10, 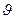 =
= 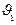 =1;
=1; 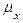 (
(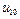 )=0,
)=0,  (
(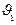 )=0.1;
)=0.1; 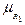 (
(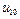 ,
, 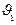 ) =1-
) =1-
-  (
(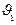 ) = 0.9 и т.д.
) = 0.9 и т.д.
При любых текущих 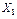 =
=  ,
, 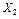 =
=  по формулам (10.3), (10.2) находим текущие нечеткие множества
по формулам (10.3), (10.2) находим текущие нечеткие множества 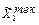 ,
, 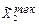 . Для нахождения
. Для нахождения 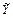 =
= 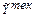 воспользуемся формулой “композиционного вывода”
воспользуемся формулой “композиционного вывода”
 =
= 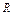 (
(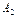 (
(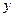 ))=
))= 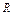 (
(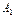 (
(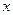 ))o
))o  (
(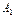 (
(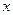 ),
), 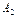 (
(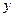 ))=
))=
=  o
o  (
(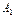 (
(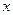 )
) 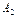 (
(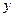 ))=
))= 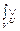 (
(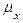 (
(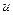 )Ù
)Ù 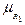 (
(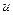 ,
, 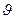 ))/
))/ 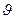 . (10.8)
. (10.8)
В качестве входного параметра для определения угла поворота манипулятора-сортировщика вводим нечеткое множество  , формирующее лингвистическую переменную ”КАЧЕСТВО2” в виде тройки
, формирующее лингвистическую переменную ”КАЧЕСТВО2” в виде тройки
 ={<
={<  ,
,  ,
,  > },
> },  Î
Î 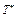 (
( ),
),  =
= 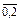 .
.
Значения переменной ”КАЧЕСТВО2” показаны в табл. 10.6. Для
Таблица 10.6. Значения переменной " КАЧЕСТВО2"
| Значение переменной ”КАЧЕСТВО2”
|  Î Î 
|
| Неустранимый дефект
|
|
| Возможна повторная обработка
|
|
| На следующую операцию
|
|
отображения  ®
®  зададим следующее. Пусть
зададим следующее. Пусть  =
=  È
È  È
È  . При этом
. При этом  Ç
Ç  Ç
Ç  =Æ, например,
=Æ, например,  ={0, 1, …, 4},
={0, 1, …, 4},  = {5, 6, 7},
= {5, 6, 7},  ={8, 9, 10}.
={8, 9, 10}.
Отметим, что $  Î
Î  ½
½  (
( )=
)= 
 (
(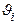 ) – “сильнейший” (с наибольшим значением
) – “сильнейший” (с наибольшим значением  (
(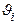 )). Осуществим переход, связывающий множества
)). Осуществим переход, связывающий множества  ,
,  ,
,  с тремя положениями манипулятора-сортировщика:
с тремя положениями манипулятора-сортировщика:
 0, если
0, если  Î
Î  ,
,
 = 1, если
= 1, если  Î
Î  , (10.9)
, (10.9)
2, если  Î
Î  .
.

(

)|
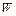
}. После выполнения п.1 находим
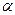
= {
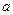
|

,
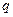
(
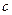
,

(

),
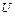
)|
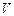
}. Пункт 2 дает
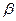
= {
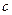
|
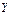
,

(

)|
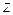
,

(

)|
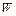
}. Результатом п.3 является
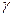
={
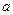
|

,
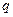
(
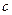
,

(

),
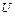
)|
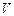
,
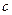
|
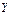
,

(

)|
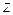
,

(

)|
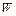
}. Очевидно, что применение к литералу последовательно замен
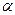
и
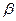
дает такой же результат, что и применение замены
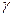
.
В общем случае 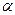 o
o 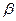 ¹
¹ 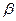 o
o 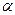 . Композиция замен ассоциативна: (
. Композиция замен ассоциативна: (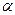 o
o 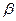 )o
)o 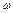 =
= 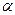 o(
o(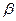 o
o 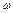 ).
).
Множество выражений {  } = {
} = {  } является унифицируемым, если существует такая замена (унификатор), что все
} является унифицируемым, если существует такая замена (унификатор), что все 
 оказываются идентичными. Пример:
оказываются идентичными. Пример:  = {
= { 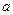 |
|  ,
, 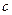 |
| 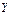 ,
, 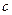 |
| 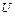 ,
,  |
| 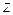 ,
,  |
| 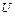 ,
, 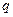 (
( )|
)| 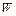 },
},
{  } ={
} ={  (
( ,
,  (
(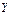 ),
),  (
( )),
)),  (
( ,
,  (
( ),
),  (
( )),
)),  (
( ,
,  (
(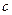 ),
), 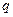 (
(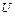 )),
)),  (
( ,
,
 (
(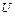 ),
), 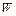 )}. Для
)}. Для 
 имеем:
имеем: 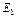
 =
=  (
(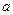 ,
,  (
(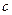 ),
), 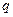 (
( )),
)), 
 = =
= =  (
(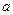 ,
,  (
(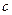 ),
), 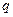 (
( )), …. Значит,
)), …. Значит,  - унификатор.
- унификатор.
Может существовать множество унификаторов  для {
для {  }. Простейшим унификатором
}. Простейшим унификатором  множества {
множества {  } называют такой, что для любого
} называют такой, что для любого  существует дополнительная замена
существует дополнительная замена  такая, что
такая, что  =
=  o
o  . Для последнего примера
. Для последнего примера  = {
= { 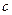 |
| 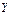 ,
, 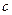 |
| 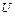 ,
,  |
| 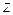 ,
,  |
| 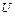 ,
, 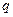 (
( )|
)| 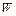 },
},  =
=  o{
o{ 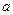 |
|  }.
}.
 (
( )|
)| 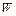 }. После выполнения п.1 находим
}. После выполнения п.1 находим 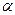 = {
= { 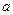 |
|  ,
, 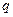 (
(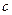 ,
,  (
( ),
), 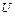 )|
)| 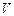 }. Пункт 2 дает
}. Пункт 2 дает 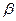 = {
= { 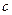 |
| 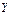 ,
,  (
( )|
)| 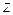 ,
,  (
( )|
)| 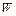 }. Результатом п.3 является
}. Результатом п.3 является 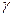 ={
={ 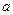 |
|  ,
, 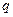 (
(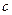 ,
,  (
( ),
), 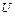 )|
)| 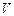 ,
, 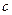 |
| 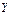 ,
,  (
( )|
)| 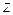 ,
,  (
( )|
)| 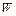 }. Очевидно, что применение к литералу последовательно замен
}. Очевидно, что применение к литералу последовательно замен 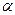 и
и 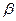 дает такой же результат, что и применение замены
дает такой же результат, что и применение замены 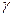 .
.

 ) аргументов, принимающая значения 1 (истина) и 0 (ложь) (
) аргументов, принимающая значения 1 (истина) и 0 (ложь) ( ”, …;
”, …; ,
,  Ú
Ú  =малый = 1/0+0.5/1+0/2.
=малый = 1/0+0.5/1+0/2. (
(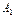 (
( )
) 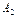 (
(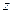 ))=(
))=( ´
´ 
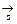
 ´
´ 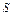 обозначает
обозначает  (
( )
)  (
( ))Ù ((1-(
))Ù ((1-(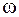 ))
))  1, если
1, если  (
( (
(
 , определяющее угол поворота, в соответствии с текущим
, определяющее угол поворота, в соответствии с текущим  по аналогии с
по аналогии с  - (10.8):
- (10.8):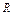 (
(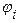 связано с параметром
связано с параметром 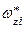 ,
,
 ),
),  =
= 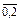 . Подставляя
. Подставляя  [(
[( (
( ] ê, (10.16)
] ê, (10.16) (Ø
(Ø  Ù
Ù  Ù 1
Ù 1
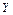
 (
(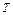 (
(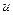 =
=  =9,
=9, 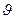 =
= 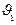 =1;
=1; 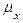 (
( (
(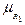 (
( ,
, 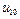 =10,
=10, 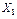 =
=  ,
, 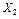 =
=  по формулам (10.3), (10.2) находим текущие нечеткие множества
по формулам (10.3), (10.2) находим текущие нечеткие множества 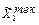 ,
, 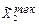 . Для нахождения
. Для нахождения 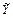 =
= 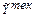 воспользуемся формулой “композиционного вывода”
воспользуемся формулой “композиционного вывода”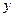 ))=
))= 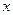 ))o
))o  (
( o
o 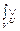 (
( ={<
={<  ,
, 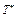 (
( Î
Î  ®
®  È
È  È
È  . При этом
. При этом  Î
Î 
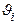 ) – “сильнейший” (с наибольшим значением
) – “сильнейший” (с наибольшим значением  0, если
0, если  = 1, если
= 1, если 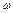 =
=  } = {
} = {  } является унифицируемым, если существует такая замена (унификатор), что все
} является унифицируемым, если существует такая замена (унификатор), что все  оказываются идентичными. Пример:
оказываются идентичными. Пример:  |
| 
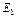

 множества {
множества {  такая, что
такая, что 


