Нечеткие множества
ОБщие положения  - базовое универсальное множество элементов - базовое универсальное множество элементов 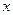 , ,  - подмножество в - подмножество в  , т.е. , т.е.  Ì Ì  . Принадлежность элемента . Принадлежность элемента 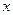
Соединение двух списков. Соединение двух списков X и Y может быть представлено как операция, обратная разделению списков. Функция присоединения называется append. Программа, реализующая эту функцию, имеет следующий вид: 10 append([ ], L, L). 20 append([X | L1], L2, [X |L3 ]): - append(L1, L2, L3). Пример. Введем запрос: append([a, b.c], [d, e, f], L), где L – неизвестный искомый список. В первом цикле решения задачи, так как [a, b.c]¹ [ ], унификация запроса (исходное состояние стека вопросов) возможна только с правилом 20: [X | L1]=[a, b.c] (т.е. X=a, L1=[b, c]), L2=[d, e, f], [X |L3 ]=L. Новоесостояние стека вопросов: append=([b, c], [d, e, f], L3). Во втором цикле унификация последнего предложения возможна также только с правилом 20. Вводя новые обозначения для переменных, имеем: X=X.1=b, L1=L1.1=[c], L2=L2.1=[d, e, f], [X1 | L3.1]=L3. Новое состояниестека: append=([c], [d, e, f], L3.1). В третьем цикле аналогично изложенному получим X.2=c, L1.2=[ ], L2.2=[d, e, f], [X2 | L3.2]=L3.1. Состояние стека: append=([ ], [d, e, f], L3.2). В четвертом цикле последний литерал унифицируется с фактом 10 программы: L=[d, e, f] (второй аргумент) и L=L3.2 ( третий аргумент).Следовательно, L3.2=[d, e, f] и состояние стека становитсяравным append=([ ], [d, e, f], [d, e, f]) – конкретный факт 10.Освобождаем стек и двигаемся по цепочке целей назад: L3.1=[X2 | L3.2]=[c, d, e, f], L3=[X1 | L3.1]=[b, c, d, e, f], L=[X | L3]=[a, b, c, d, e, f]. Исходное состояние стека становится конкретным фактом 10. Вариант ответа найден. Дополнительная унификация предпоследнего стекового литерала append=([ ], [d, e, f], L3.2) ужес правилом 20 невозможна, так как в данном литерале первый аргумент “[ ]” нельзя представить сочетанием головы и хвоста. Данная программа позволяет решить обратную задачу: определить при известном списке одну из его частей: append(L, [d, e, f], [a, b, c, d, e, f]), где L – неизвестный присоединенный список. Последовательность поиска ответа такова. Первый цикл. Унификация литерала append(L, [d, e, f], [a, b, c, d, e, f]) с фактом 10 - append([ ], L, L) - невозможна, так как [d, e, f]¹ [a, b, c, d, e, f]. Унификация с правилом 20 дает [X | L1]=L, L2=[d, e, f], [X | L3]=[a, b, c, d, e, f], X=a, L3=[b, c, d, e, f]. Новоесостояние стека: append=(L1, [d, e, f], [b, c, d, e, f]). Второй цикл. Как и в первом цикле, с учетом переименования имеем: [X.1 | L1.1]=L1, L2.1=[d, e, f], [X.1 | L3.1]=[b, c, d, e, f], X.1=b, L3.1=[c, d, e, f]. Состояние стека: append=(L1.1, [d, e, f], [c, d, e, f]). Третий цикл. Аналогично: [X.2 | L1.2]=L1.1, L2.2=[d, e, f], [X.2 | L3.2]=[c, d, e, f], X.2=c, L3.2=[d, e, f]. Состояние стека: append(L1.2, [d, e, f], [d, e, f]). Четвертый цикл. Последний литерал унифицируется с фактом 10: [ ]= =L1.2. Послеунификациипоследнее состояние стека становится конкретным. Двигаемся назад по цепочке целей: L1.1=[ X.2 | L1.2]=[c], ЭС и ее тестировании. 1. Идентификация. На данном этапе определяются задачи, участники разработки и имеющиеся ресурсы. 2. Концептуализация. Выделяются ключевые понятия, отношения и характеристики, описывающие процесс решения задачи. Определяются типы исходных данных и стратегии решения. 3. Разбивка ЭС на модули для детальной проработки. Здесь следует выделить два способа разбивки: 3.1. Структурное программирование, при котором осуществляется декомпозиция системы по методу “сверху-вниз”. Такой метод называется каскадным. Он обеспечивает линейность выполнения этапов разработки и использование процедурных языков программирования. Главный недостаток – программирование можно начинать только после завершения проектирования. Это приводит к сложностям модернизации системы, так как почти всегда в этом случае надо начинать с начала. 3.2. Объектно-ориентированная декомпозиция, заключающаяся в представлении ЭС в виде совокупности классов и объектов предметной области. Процесс разработки принципиально носит итерактивный характер, приводящий к эволюции системы, постепенному улучшению ее свойств. В любой момент могут вводиться новые классы и объекты, разрабатываться сценарии. Могут быть быстро разработаны прототипы ЭС, протестированы методы и свойства, взаимоотношения объектов. Коды программы могут генерироваться автоматически. Нет строгой последовательности разработки, этот метод назвали возвратным. Он позволяет распараллелить работы, что ускоряет проектирование. Разработанные компоненты легко повторно использовать, что также экономит время. 4. Формализация. Все выявленные отношения и связи выражаются на формальном языке. 5. Выполнение - компоновка всей ЭС. 6. Отладка и тестирование: 6.1. Тестирование на основе концепции “черного ящика”: набор тестируемых ситуаций генерируется без учета используемых в системе методов решения задач. 6.1.1. Случайное тестирование: тестируемые ситуации выбираются случайным образом из пространства входных наборов данных. 6.1.2. Выборочное тестирование входов: пространство входных наборов данных разбивается на выборки, для которых определяются ситуации для тестирования. 6.1.3. Выборочное тестирование выходов: тестируемые ситуации определяются на основе выборок, сформированных для выходных наборов данных. 6.2. Тестирование на основе концепции “белого ящика”: тестируемые ситуации учитывают внутреннюю структуру системы. 6.3. Тестирование полноты базы знаний. 6.3.1. Поиск конфликтных правил, приводящих к различным ситуациям. 6.3.2. Поиск избыточных правил. 6.3.3. Поиск продукционных правил. 7. Опытная эксплуатация: Рассмотрим запрос: меньший([b, c, a, e], L), где L – наименьший элемент в списке [b, c, a, e]. Процедура поиска элемента: Первый этап. Унификация с 10 невозможна, так как [b, c, a, e] – список, а X – элемент. Унификация с 20 допустима при [X, Y|Z]=[b, c, a, e], R=L, т. е. X=b, Y=c, Z=[a, e], R=L. Новое состояние стека: b< =c, меньший([b|[a, e]], L) (слагаемое X> Y, меньший([Y|Z], R) правила 20 не учитывается вследствие ложности неравенства X> Y). Первое неравенство не требует доказательства, поэтому в стеке остается: меньший([b|[a, e]], L). Второй этап. Унификация литерала меньший([b|[a, e]], L) с 10 невозможна. Унификация с 20 дает: [X.1, Y.1|Z.1]=[b|[a, e]], R=L.1, т.е. X.1=b, Y.1=a, Z.1=[e], R=L.1. Новое состояние стека: b> a, меньший([a|[e]], L.1). После удаления факта b> a в стеке остается: меньший([a|[e]], L.1). Третий этап. Унификация последнего предложения с литералом 10 невозможна. Унификация с 20 дает: [X.2, Y.2|Z.2]=[a|[e]], R=L.2, т.е. X.2=a, Y.2=e, Z.2=[ ], R=L.2. Состояние стека, так как a< e, равно: меньший([a|[ ]], L.2). Четвертый этап. Унификация литерала меньший([a|[ ]], L.2) с фактом 10 возможна при L.2=a. Возврат назад по цепочке целей к исходному состоянию стека дает ответ: L=R=a. Других решений нет. Выбор наибольшего элемента. Аналогичен предыдущему поиску при замене знаков неравенств “< ”, “> ” соответственно на “> ” и “< ”. Перевод одного списка в другой. Формально простой метод перевода заключается в поиске для каждого слова исходного текста соответствующего ему слова из словаря. Рассмотрим пример базы знаний: 10 перевести([ ], [ ]). 20 перевести([С_А|Ф_А], [С_Р|Ф_Р]): - словарь(С_А, С_Р), перевести(Ф_А, Ф_Р). 40 словарь(“I”, ”я”). 50 словарь(“study”, ”изучаю”). 60 словарь(“language”, ”язык”). 70 словарь(“PROLOG”, ”Пролог”). 80 словарь(“in”, ”в”). 90 словарь(“the university”, ”университете”). Здесь записано правило перевода 20: выбрать первое слово С_А английской фразы Ф_А, найти ему соответствующее русское слово С_Р в словаре и поставить в начало русского перевода Ф_Р. Введем запрос: перевести([“I”, ”study”, ”language”, ”PROLOG”, ”in”, ”the university”], P)..Процедура перевода: Первый цикл. Унификация запроса с фактом 10 невозможна. Унификация с правилом 20 дает: [С_А|Ф_А]=[“I”, ”study”, ”language”, ”PROLOG”, ”in”, ”the university”], [С_Р|Ф_Р]=P, т.е. С_А=“I”, Ф_А=[”study”, ”language”, ”PROLOG”, ”in”, ”the university”]. Новое состояние стека вопросов: словарь=(“I”, Р), перевести([”study”, ”language”, ”PROLOG”, ”in”, ”the university”], Ф_Р).
=. Тогда для S=[XY] из уравнения S=ST находим
[XY] = [XY], что дает X=7/16, Y=8/15. Кроме упомянутых ЭС, можно также выделить: изолированные ЭС, не способные взаимодействовать с другими программными системами, и интегрированные ЭС, взаимодействующие с другими программными системами; закрытые ЭС, работающие только в программной среде фирмы-разработчика, и открытые ЭС, ориентированые на использование в разных программных средах; централизованные ЭС, территориально располагаемые на серверах, и децентрализованные ЭС, использующиеся на периферийных устройствах. Часто ЭС классифицируют по типу решаемых ими задач. В этом случае можно выделить ЭС интерпретации, прогноза, диагностики, проектирования, планирования, мониторинга, обучения, управления и т.д.
|






