Семантическая сеть
Если в иерархической модели (рис. 3.1) запись-потомок может иметь только одну запись-предка (информация о связях), то в сетевой модели запись-потомок может иметь произвольное число записей-предков. В основе семантической модели лежит граф, собирающий вокруг одного узла всю информацию по данному узлу. Семантическая сеть состоит из множества объединенных концептуальных графов, каждый из которых соответствует некоторой логической формуле со своими именами и аргументами предикатов, связанными друг с другом по установленным правилам. Пример концептуального графа логической формулы “ Поставка(Интеграл, Луч, Схема 14)” (смысловая трактовка формулы и правило моделирования формулы не рассматриваются) приведен на рис.4.1.Аргументы изображены прямоугольниками, а предикат – скругленным контуром. Первые два аргумента связаны с третьим через имя предиката. При изменении отношений между элементами сети связи между ними будут модифицироваться соответствующим образом. Преобразование семантических сетей из совокупности
1-й аргумент
3-й аргумент
предиката
2-й аргумент
Рис.4.1. Концептуальный граф формулы “ Поставка(Интеграл, Луч, Схема 14)”
концептуальных графов можно осуществить с помощью специальных правил. Правило коньюнкции: если узлы-концепты 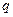 содержит два идентичных содержит два идентичных
Кроме этого, СЭС обычно включает интерфейс связи с внешними источниками информации, подсистему приобретения знаний, диалоговый интерфейс и т.д. Главный недостаток СЭС – непредсказуемость времени на их выполнение. Динамические ЭС (ДЭС). Учитывают изменение компонентов во время решения задачи (например, системы реального времени). Поэтому они имеют средства на сокращение перебора, оперативные алгоритмы реакции на непредвиденные ситуации. ДЭС включает СЭС, подсистему моделирования внешнего мира (ПМВМ), интерфейс связи с внешним миром (ИСВМ):
Один из подходов к моделированию внешнего мира основывается на процессе Маркова. Этот процесс: - имеет конечное число возможных состояний, - может находиться в одном состоянии в одно время, - последовательно переходит из одного состояния в другое с течением времени, - вероятность перехода зависит от только что произведенного состояния (отсутствие последействия). Примером процесса Маркова является диаграмма перехода из одного состояния в другое в соответствии со следующей матрицей переходов (Т):
Будущее
 S PJ i =1 (вероятностный вектор). S PJ i =1 (вероятностный вектор).
Если исходное состояние процесса квалифицировать строкой состояния S1=[P1P2…Pn], где S Pr =1 (rÎ {1, 2, …n}), то будущее S2=S1T. При последовательном умножении SkT (k=1, 2, …)для T, содержащей только положительные элементы (регулярная матрица переходов), в итоге получим S=ST, где S – матрица устойчивого состояния (независимо от начального S1). Для примера используем матрицу T= ”я”=Р. В стеке остается: перевести([”study”, ”language”, ”PROLOG”, ”in”, ”the university”], Ф_Р). Третий цикл. Унификация стекового литерала возможна только с правилом 20: [С_А.1 | Ф_А.1] = [”study”, ”language”, ”PROLOG”, ”in”, ”the university”], [С_Р.1 | Ф_Р.1] = Ф_Р, т.е. С_А.1 = ”study”, Ф_А.1 = [”language”, ”PROLOG”, ”in”, ”the university”] и т.д.до исчерпания всех слов. При этом последнее состояние стека унифицируется с фактом 10. Возврат по цепочке целей назад увеличивает длину искомой переменной P = =[ С_Р | Ф_Р ], Ф_Р=[С_Р.1 | Ф_Р.1], … до следующей предельной величины: P= = [“я”, ”изучаю”, ”язык”, ”Пролог”, ”в”, “университете”]. Других решений нет. Удаление заданного элемента из списка. Проводится путем сравнения элемента с первым элементом исходного списка или его части и удаления из них элемента, совпадающего с заданным. Операция может быть многоэтапной и основывается на двух правилах: 1) если удаляемый элемент E совпадает с головой списка [E | Y], то надо оставить его хвост Y: удалить(E, [E | Y], Y); 2) если удаляемый элемент E не совпадает с головой списка, то надо найти его в хвосте и удалить: удалить(E, [X |Y ], [X |Z ]): - удалить(E, Y, Z). Указанные факт и правило образуют программу удаления заданного элемента E из списка [X |Y ]. Сортировка элементов списка. Используется метод последовательного сравнения смежных элементов: в списке находят наименьший элемент, если сортировка идет по возрастанию (или наибольший, если по убыванию), добавляют его в голову другого списка и удаляют из первого списка. Далее этот процесс продолжают с оставшимся подсписком до исчезновения в нем элементов: 10 сортировать([ ], [ ]). 20 сортировать(L, [M |R ]): - меньший(L, M), удалить(M, L, Q), сортировать(Q, R), !. Пример запроса: сортировать([e, t, r, a, b], S), где S – искомый список. Процедура сортировки повторяет вышеприведенные этапы. Первый цикл. Унификация с правилом 20 возможна при L=[e, t, r, a, b], S=[M | R]. Новое состояние стека вопросов: меньший([e, t, r, a, b], M), удалить(M, [e, t, r, a, b], Q), сортировать(Q, R),!. А-1.2.4. Знакомство с понятиями (1) А-2. Арифметика А-2.1. Сложение однозначных чисел (1) А-2.2. Сложение многозначных чисел (1) А-2.3. Вычитание однозначных чисел (1) А-2.4. Вычитание многозначных чисел (1) А-2.5. Умножение однозначных чисел (1) А-2.6. Умножение многозначных чисел (1) А-2.7. Деление без остатка (1) А-2.8. Деление с остатком (1) Б. Биология и физиология Б-1. Наследственные факторы Б-1.1. Неспособность к обучению родителей (1) Б-1.2. Неспособность к обучению родных братьев и сестер (не близнецов) (1) Б-1.3. Неспособность к обучению близнецов (1) Б-1.4. Хромосомные аномалии или наследственные болезни в семье (1) В. Психология В-1. Самоуверенность В-1.1. Отказ от работы (1) В-1.2. Необоснованность поступков (1) В-1.3. Позерство (1). В ЭС устанавливаются уровни принятия решения о способности учащегося. При определении решения (вывода) суммируются все полученные веса подразделов (фактов). Если полученная сумма равна или превышает уровень принятия решения, можно говорить о затруднениях в усвоении материала. Уровней принятия решений можно сделать несколько. Тогда можно говорить о способности учащегося в численном или лингвистическом масштабе. В процессе освоения ЭС весовые коэффициенты могут изменяться в ту или другую сторону, обеспечивая приоритетность подразделов применительно к конкретной ситуации.
|


 Имя
Имя

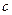 1 и
1 и 

 Здесь P – вероятность, причем
Здесь P – вероятность, причем


 Настоящее
Настоящее
 Т
Т



