Интерпретатор Пролога
Пролог находит в базе знаний факт, соответствующий первой цели (подвопросу) и пытается подобрать факт, удовлетворяющий остальным целям таким образом, чтобы одна и та же переменная имела одно и то же значение при поиске одного варианта решения. Возврат для поиска новых решений идет обратно по цепочке целей. Рассмотрим программу: domains имя=symbol predikates отец(имя, имя) дед(имя, имя) clauses 10 отец(алексей, владимир). 20 отец(андрей, алексей). 30 дед(X, Y): - отец(X, Z), отец(Z, Y). Пусть задан вопрос: дед(X, Y). Он помещается в стек вопросов (целей) с состоянием 40 дед(X, Y). В первом цикле интерпретатор просматривает сверху вниз пункты программы 10-30. Он пытается унифицировать первый литерал из стека (в данном примере литерал всего один) с первыми литералами предложений 10-30. Только правило 30 в нашем примере может быть унифицировано с предложением 40. Перед унификацией интерпретатор переименовывает переменные в пункте 30: X ® X1, Y ® Y1, Z ® Z1. Унификация предложений 40 и 30 требует замену: X вместо X1, Y вместо Y1. После унификации литерала из стека вопросов 40 и правила 30 содержимое стека замещаетсяусловной частью правила 30: 40a отец(X, Z1), отец(Z1, Y). 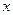 есть есть  , то , то 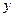 есть есть 
Пр2:
III. Пр1: если
Сл:
IV-1. Пр1: если Пр2:
IV-2. Пр1: если Пр2:
где “Пр” – предпосылка, “Сл” – следствие, Условие-неравенство: Пример:
Проверим правило-критерий I. Для этого сначала найдем бинарное отношение
При описании предложений типа фактов на языке Пролог необходимо соблюдать правила: - имена объектов (сущностей) и отношений состоят из латинских букв, цифр, знаков подчеркивания и начинаются со строчной буквы; - первым в предложении указывается имя отношения, за которым в скобках указываются имена объектов, разделяемых запятыми; - факт заканчивается точкой, порядок перечисления объектов в скобках произволен, но постоянен. Имена объектов в круглых скобках называются аргументами, а имя отношения – предикатом. Имена объектов и отношений выбираются произвольно. Отношения могут иметь произвольное число аргументов. Аргументы могут быть представлены константами или переменными. Пример (для удобства чтения наряду с латинскими будем использовать русские буквы): вопрос “ отец(виктор, X) ” переводится как “отцом каких детей является Виктор? ”. Для нахождения ответа просматриваются имена всех имеющихся в наличии объектов, отец которых – Виктор. Ответов может быть несколько, например: 1) X =таня, 2) X=оля. Подвопросы в предложениях отделяются запятыми (союз “и”). Примеры: 1. нравится(виктор, анна), нравится (анна, виктор) – нравятся ли Виктор и Анна друг другу?. 2. нравится(виктор, X), нравится(анна, X) – что нравится обоим – Виктору и Анне?. Факты в программе на языке Пролог записываются в разделе clauses. Пример программы на языке Пролог, содержащей факты: domains имя=symbol predikates отец(имя, имя) муж(имя, имя) clauses отец(виктор, таня). отец(виктор, оля). отец(виктор, даша). отец(владимир, виктор). отец(владимир, сергей). муж(виктор, анна). муж(владимир, люда). Здесь domains - определение аргументов, predikates - формат предикатов, clauses – факты и правила. На запрос отец(X, Y) Пролог отвечает в соответствии с принципом поиска всех решений: X=виктор, Y=таня X=виктор, Y=оля 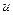 = =  =1, =1,  = =  =0; =0;  ( ( )=0.8, )=0.8, 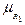 ( ( , ,  )=0; )=0;  =0.8Ù 0=0 и т. д. =0.8Ù 0=0 и т. д.
50. Очевидно, что 02. 12.
42. 52.
|

 Сл:
Сл:  Пр2:
Пр2:  Сл:
Сл:  Сл:
Сл:  (
( (
(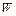 ” =
” =  , “более или менее
, “более или менее  (
( (
(
 (
(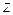 .
. ,
,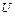 =
= 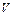 =0+1+2+3+4+5+6+7+8+9+10,
=0+1+2+3+4+5+6+7+8+9+10, (
(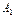 (
(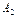 (
(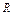 (
(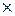

 (
( (
(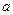 =
=  =
= 
 =5,
=5, 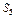 =0Ù 1=0 и т. д.
=0Ù 1=0 и т. д. (
( [
[  )=0. Далее:
)=0. Далее: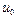 =0,
=0,  =2;
=2;  .
.
 =4,
=4,  =0.2Ù 1=0.2.
=0.2Ù 1=0.2. =0. Для этих пунктов
=0. Для этих пунктов  (
( )]=0.2. После нахождения всех значений
)]=0.2. После нахождения всех значений 


