Прямой и обратный поиск. Поиск новых знаний в продукционных моделях может быть прямым и обратным
Поиск новых знаний в продукционных моделях может быть прямым и обратным. Рассмотрим указанные методы применительно к теории 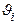 - функции принадлежности элементов нечеткого множества - функции принадлежности элементов нечеткого множества 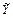 , соответствующего найденному значению лингвистической переменной. , соответствующего найденному значению лингвистической переменной.
Зная Таблица 10.5. Матрици отношений
Пример расчета: 00. 10. = 0.9, для первого элемента из ………………………………………………………………………………….. 100. 01.
 Ø Ø 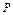 ( ( )Ú Ø )Ú Ø  ( ( , , 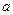 )Ú )Ú 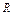 ( ( , ,  )Ú )Ú 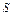 ( (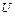 ), ),
Ø Символы переменных в соответствии с законом немых переменных можно изменить так, чтобы они появлялись не более, чем в одном из обособленных предложений, что дает формальное разделение (независимость) переменных в предикатах одного предложения относительно других предложений:
Ø Такая замена переменных позволяет в ряде случаев рассматривать множество связанных предложений независимо друг от друга, что упрощает их машинную обработку при поиске новых знаний. Если литерал в любом предложении не содержит никакой переменной, он называется конкретным. Дизъюнкция таких литералов является конкретным предложением. Цель анализа логических выражений обычно состоит именно в том, чтобы свести их к тем или иным конкретным литералам и предложениям, представляющим собой известные факты.
|

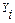 =
= 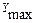 , а из (10.7) по аналогии с
, а из (10.7) по аналогии с  имеем
имеем 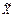 ,
,  (
(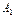 (
(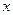 )
) 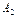 (
(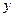 )) по (10.5), где
)) по (10.5), где 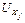 =
=  ,
, 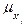 (
(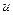 )=
)= 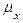 (
(
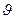
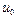 =0,
=0,  =0; из ранее определенных нечетких множеств
=0; из ранее определенных нечетких множеств  (
( )=0. Тогда из (10.5) получаем
)=0. Тогда из (10.5) получаем 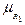 (
( =1,
=1, 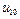 =10,
=10, 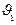 =1;
=1; 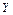 ,
, 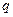 (
(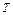 (
(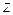 )Ú Ø
)Ú Ø 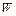 )Ú Ø
)Ú Ø 


