Операции
1. Арифметические операции: “+”, “-”, “*”, “/”. Пример: расстояние1=расстояние2+расстояние3. Порядок аргументов в выражениях значения не имеет. 2. Функции: X mod Y – остаток от деления X на Y; X div Y - целая часть от деления X на Y; abs(X) – абсолютная часть числа X; exp(X) – e в степени X; sgrt(X) – квадратный корень из X; sin(X), cos(X), tg(X), arctg(X). Приоритеты: 1) “+”, “-“; 2) “*”, “/”; 3) mod, div; 4) одноместные “+”, “-“. 3. Логические операции: - умножение – “, ”, - сложение – “; ”, - отрицание – “not” – предикат. 4. Операции отношения: “> ”, “> =”, “< ”, “< =”, “=”, “< > ” или “> < ”. Используем некоторые из перечисленных операций, например для вычисления факториала Y от X: предикат fact(X, Y). Так как Пролог обрабатывает все возможные варианты, надо указать условие останова поиска вариантов решения, например X> 1. Тогда программа вычисления факториала будет иметь следующий вид: predicates fact(real, real) clauses 10 fact(1, 1). 20 fact(X, Y): - X> 1, Z=X-1, fact(Z, X1), Y=X*X1. Запрос оформим как fact(5, X). Во время первого цикла решения задачи Пролог анализирует стек вопросов, состояние которого есть сам запрос. Очевидно, что исходное предложение-запрос после сравнения его с фактом 10 и правилом 20 программы может быть унифицировано только с правилом, так как в факте 10 первый аргумент “1” не соответствует первому аргументу “5” запроса. После унификации имеем для программного правила X=5, Y=X. Далее стек вопросов должен быть обновлен условной частью правила 20: X> 1, Z=X--1, fact(Z, X1), Y=X*X1. Анализ составляющих стека с учетом предыдущих замен переменных дает: 5> 1, Z=5-1=4, fact(4, X1), X=5*X1 или, после отбрасывания из стека конкретных фактов, fact(4, X1), X=5*X1.
Максиминная композиция
 ( ( ( ( , ,  )). Пример: )). Пример:
Порядок расчета
Очевидно, что любому набору пар
|


 o
o  , где
, где  Ì
Ì  ´
´ 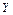 ,
, 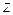 :
: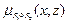 =
=  (
(


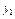






 =
= 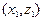 . Тогда:
. Тогда: (
( ,
,  ) =
) =  ,
, 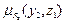 ) =
) = 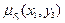 ,
,  ) =
) =  (0.1, 0.4, 0.7) = 0.7 и т. д.
(0.1, 0.4, 0.7) = 0.7 и т. д. /
/ 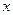 ,
,  /
/  можно дать словесные (лингвистические) определения. Это увязывает нечеткую логику с мышлением человека (хороший, плохой, очень, не очень, более или менее, неизвестно), так как иначе трудно оценить состояние объекта, характеризующегося указанными наборами. Нечетких логик много. Пример: нечеткая (многозначная) логика
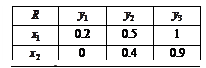
можно дать словесные (лингвистические) определения. Это увязывает нечеткую логику с мышлением человека (хороший, плохой, очень, не очень, более или менее, неизвестно), так как иначе трудно оценить состояние объекта, характеризующегося указанными наборами. Нечетких логик много. Пример: нечеткая (многозначная) логика  (табл. 10.1, где
(табл. 10.1, где 
 =
= 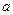 =
= 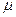 ) логических посылок
) логических посылок  и
и  ).
).


