Унификация
При анализе множества любых предложений с целью получения новых знаний переменные в них необходимо преобразовать таким образом, чтобы стало возможным сопоставление исходных предложений с последующим выводом нового предложения. Одной из таких операций является зависимая замена переменных, противоположная ранее рассмотренной. Такая замена переменных в литералах с целью их эквивалентных преобразований называется унификацией. Заменой = { Композицией двух замен 1) применяют 2) исключают из 3) собирают пары, полученные в пп.1, 2. 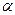 = { = { 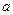 | |  , , 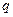 ( (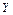 , , 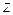 , , 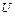 )| )| 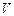 }, }, 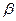 = { = {  | |  , , 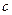 | | 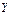 , ,  ( ( )| )| 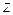 , ,  ( (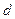 )| )| 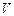 , ,
где
Угол поворота манипулятора-сортировщика выражается в виде нечеткого множества
Значения переменной “УГОЛ” приведены в табл.10.7. Переменная
Таблица 10.7. Значения переменной " УГОЛ"
находится обычным путем:
Зададим углы поворота манипулятора
-1)
По аналогии с (10.5) для построения нечеткого бинарного отношения, характеризующего логическую связь между качеством изделия и углом “Если Как и ранее, используя соответствующие формулы (10.10)-(10.13), табл.10.6 для производит другие ПФ. 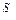 называются аксиомами. называются аксиомами.
|

 (возможно использование и других символов) называют конечное множество упорядоченных пар {
(возможно использование и других символов) называют конечное множество упорядоченных пар { 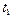 |
| 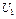 , …,
, …, 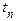 |
| 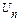 } =
} = 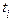 |
| 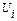 означает, что переменная
означает, что переменная 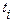 . Применение
. Применение  обозначают как
обозначают как  (
(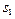 =
=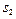 = {
= { 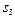 = {
= {  (
(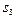 =
= 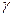 =
=  =
= 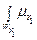 (
( )/
)/ 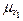 (
( )=1-
)=1- 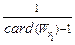 ô
ô  ô,
ô,  =
= 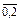 . (10.11)
. (10.11) , которое формирует лингвистическую переменную “УГОЛ” в виде тройки
, которое формирует лингвистическую переменную “УГОЛ” в виде тройки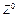 ={<
={< 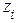 ,
,  ,
, 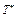 (
( ),
),  Î
Î 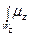 (
(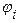 Î [900, 2700], т. е.
Î [900, 2700], т. е. 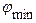 =900,
=900, 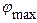 =2700. В соотношении (10.12) функция принадлежности
=2700. В соотношении (10.12) функция принадлежности  (
(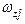 ) рассчитывается по формуле
) рассчитывается по формуле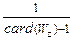 ê
ê  [(
[( (
(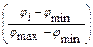 ] ê,
] ê, 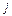 =
= 


