Семантика языка предикатов первого порядка
Всякая формула имеет определенный смысл только тогда, когда существует какая-либо ее интерпретация на области Значение любой ПФ на области Некоторые ПФ эквивалентны друг другу. Ниже представлена таблица 1.1 эквивалентных (построчно) ПФ. Эквивалентные ПФ совпадают независимо от их интерпретации. Формы записи ПФ разнообразны. Обычно ПФ представляются как дизъюнкция литералов. Литерал - это атом или его отрицание. Формулу, представляющую собой дизъюнкцию литералов, называют предложением (дизъюнктором). В каждом литерале отсутствуют операции (включая кванторы) и область действия знака отрицания уменьшена до одной предикатной буквы (пример: Ø (" Квантор существования в ПФ можно исключить с помощью функций Сколема. Пример ПФ: (" Все кванторы общности, имеющие свою переменную, независимо от количества и первоначального положения их в ПФ можно переместить в ее начало без изменения относительного порядка кванторов. Такая формула называется префиксной. Она состоит из цепочки кванторов (префикс) и следующей за ними матрицы (бескванторная часть). Пример: ((" Ú Ú ( Матрицу в свою очередь с помощью законов ассоциативности и дистрибутивности операций Ú и Ù можно привести к коньюнктивной нормальной форме как коньюнкцию конечного множества дизъюнкций литералов. Например: ("  900, 900, 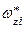 =0, =0,
2700, Пример: 00. 10. ……………………………………………………… 100. Из 00-100 и (10.2) находим 01. 11. ………………………………………………………….. 101. По 01-101 и (10.8) получаем
Информационные системы (ИС) входят в число важнейших компонентов науки и производства. Они широко используются для обучения и решения конкретных задач в различных областях человеческой деятельности: в автоматизированных системах управления (АСУ) и научных исследований (АСНИ), системах автоматизации проектирования (САПР), информационно-поисковых системах (ИПС), системах управления базами данных (СУБД), экспертных системах (ЭС), системах поддержки принятия решения (СППР) и т.д. ИС, помимо прочего, характеризуются тем, что с их помощью можно накапливать знания и опыт людей, совершенствуя работу и возможности самих ИС. Знание – это информация о свойствах и законах предметной области. Знания могут быть исходными и выводимыми, конкретными и обобщенными. Конкретные знания обычно именуют данными, а обобщенные – просто знаниями. Данные – это исходная частная информация об окружающем мире. ИС оперируют формализованными данными, которые позволяют автоматизировать сбор и хранение конкретной информации об объектах. Формализованные данные можно обработать по определенной программе. В результате обработки данных получают новые знания. Знания могут быть декларативными и процедурными. Декларативные знания представляют собой утверждения, не содержащие процедур. Декларативные знания определяют пространство статического состояния объекта. Процедурные знания – это программы обработки данных (фактов) с целью получения новой информации. Одной из главных проблем, с которой сталкиваются разработчики ИС, являются методы и формы представления знаний, минимизирующие затраты ресурсов ИС и способствующие высокой эффективности общения с ними. В первую очередь это касается моделей представления знаний.
|

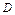 . Указанная интерпретация зависит от предметной области знания, в которой используются предикаты.
. Указанная интерпретация зависит от предметной области знания, в которой используются предикаты. (
( )). Каждый квантор в пределах области действия по закону немых переменных можно связать со своей переменной. Пример:
)). Каждый квантор в пределах области действия по закону немых переменных можно связать со своей переменной. Пример: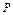 (
( (
(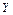 )
) 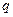 (
(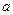 )Ú (
)Ú (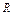 (
( )Ù (("
)Ù ((" 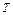 (
(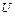 )
) 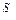 (
(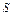 (
(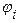 =900
=900 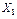 Î [3, 8] мм,
Î [3, 8] мм, 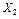 Î [100, 183]0,
Î [100, 183]0,  =5.5 мм,
=5.5 мм,  =1600. Тогда согласно (10.1) для
=1600. Тогда согласно (10.1) для 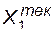 находим
находим 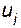 =5 (ПАРАМЕТР= среднее). Согласно (10.1) для
=5 (ПАРАМЕТР= среднее). Согласно (10.1) для  =7 (ПАРАМЕТР= почти большое). Далее рассчитываем
=7 (ПАРАМЕТР= почти большое). Далее рассчитываем  (
(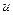 ),
), 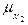 (
(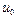 =0;
=0;  =1;
=1; 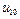 =10;
=10; 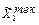 = среднее = 0.5/0+0.6/1+0.7/2+0.8/3+ +0.9/4+1/5+0.9/6+0.8/7+0.7/8+0.6/9+0.5/10,
= среднее = 0.5/0+0.6/1+0.7/2+0.8/3+ +0.9/4+1/5+0.9/6+0.8/7+0.7/8+0.6/9+0.5/10, 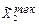 = почти большое = 0.3/0+ +0.4/1+0.5/2+0.6/3+0.7/4+0.8/5+0.9/6+1/7+0.9/8+0.8/9+0.7/10. В этом случае
= почти большое = 0.3/0+ +0.4/1+0.5/2+0.6/3+0.7/4+0.8/5+0.9/6+1/7+0.9/8+0.8/9+0.7/10. В этом случае 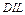 (
( =
= 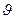 =
=  =0;
=0; 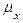 (
(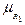 (
( (
(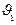 ),
), 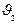 ), …. В итоге в соответствии с (10.4) имеем
), …. В итоге в соответствии с (10.4) имеем 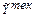 = 0.5/0+0.6/1+0.7/2+0.8/3+0.9/4+0.89/5+0.84/6+0.77/7+
= 0.5/0+0.6/1+0.7/2+0.8/3+0.9/4+0.89/5+0.84/6+0.77/7+


