И методов экспертного оценивания
Окончание табл. 1.20
Известны две меры согласованности мнений группы экспертов: дисперсионный и энтропийный коэффициенты конкордации (ДКК и ЭКК). Дисперсионный коэффициент конкордации. ДКК оценивается формулой (8). Для ее вывода проведем ряд рассуждений [9]. Пусть имеется матрица результатов ранжировки и объектов группой из m экспертов ||rij|| (j = 1, …, m; i = 1, …, n), где rij – ранг, присваиваемый j-м экспертом i-му объекту. Найдем вектор
Определим оценку дисперсии найденной последовательности в предположении, что она случайная величина
где
ДКК определяется как отношение оценки дисперсии D к максимальному значению этой оценки:
Значение W изменяется от нуля до единицы, так как 0 £ D £ D max. Найдем D max для случая отсутствия связанных рангов (все объекты различны), предварительно показав, что D зависит только от n и m (числа объектов и количества экспертов). Подставив (1) в (3), получим
Если j = const, найдем сумму рангов для j -го эксперта. Поскольку для ранжирования используются натуральные числа от 1 до n, можно записать сумму натуральных чисел от 1 до n:
Подставив (6) в (5), получим:
Из (7) видно, что величина
Введя обозначение
Тогда окончательное выражение для коэффициента конкордации (для случая отсутствия связи рангов) запишется как
максимальное значение дисперсии достигается в случае полного совпадения мнений экспертов. Минимальное значение дисперсии, которое равно нулю, достигается в случае, если эксперты дают несовпадающие мнения. Доказательство этого утверждения здесь не приводится, оно дано в [9]. При наличии связанных рангов коэффициент конкордации вычисляется по формуле
где ДКК = 1, если все ранжировки одинаковы (имеется явный сговор [7]). ДКК = 0, если все ранжировки различны (некомпетентность [7]). ДКК можно считать случайной величиной. В таком случае необходимо дать оценку значимости значения ДКК. Для больших значений n и m (при n > 7) можно использовать критерий Доказано, что величина w = m (n – 1) имеет При наличии связанных рангов (более общего случая)
Определение взаимосвязи ранжировок. Для решения задачи определения зависимости между ранжировками двух экспертов или связи между достижением двух различных целей при решении одной и той же совокупности проблем или взаимосвязи между двумя признаками используют меру, называемую коэффициентом ранговой корреляции (КРК). Характеристикой взаимосвязи множества ранжировок или целей будет являться матрица КРК. Известны КРК Спирмена и Кендалла. КРК Спирмена определяется формулой
где К 12 – взаимный корреляционный момент первой и второй ранжировок, D 1, D 2 – дисперсии этих ранжировок. Для определения взаимовлияния двух ранжировок К 12 , D 1 и D 2 вычисляются по формулам:
где n – число ранжируемых объектов; Оценки средних рангов определяются как
Проведя ряд
КРК Спирмена изменяется от –1 до +1. КРК = 1 при одинаковых ранжировках, т.е. при Определить значимость случайной величины r можно с помощью следующих формул и рассуждений. Если |r| < e, где e – пороговое значение случайной величины r для вероятности b, то оценка КРК Спирмена считается значимой. e определяется как
где n – количество объектов; y(х) – функция, обратная функции Значения функции Для определения значимости оценки КРК Спирмена можно воспользоваться критерием Стьюдента, поскольку величина Для связанных рангов КРК Спирмена имеет вид:
где r – оценка КРК Спирмена,
здесь k 1 и k 2 – количество связанных рангов в первой и второй ранжировках соответственно. КРК Кендалла при отсутствии связанных рангов определяется формулой:
где n – количество объектов; rij – ранги объектов; sign х
Сравнение (из опыта использования) обоих КРК показывает, что КРК Спирмена дает более точный результат и рассчитывается по более простой формуле, т.е. при практических расчетах он более предпочтителен.
Пример. Два эксперта провели ранжирование пяти объектов. Результаты ранжировки приведены в таблице.
КРК Спирмена Определим порог e при b = 0, 05:
Поскольку r = 0, 5 < e = 0, 98, оценка КРК является значимой.
Энтропийный коэффициент конкордации (ЭКК) определяется формулой из [9]:
где Н – энтропия, вычисляемая как
Н max – максимальное значение энтропии, Рij – оценки вероятностей j -го ранга, присваиваемые i -му объекту; Максимальное значение энтропии достигается при равновероятном распределении рангов, т. е. когда
Значение ЭКК изменяется от нуля до единицы. При W э = 0 расположение объектов по рангам равновероятно, поскольку ЭКК и ДКК дают примерно одинаковую оценку согласованности мнений экспертов при различных ранжировках. Но ЭКК позволяет обнаружить факт разделения мнений экспертов на две противоположные группы (в таком случае ЭКК = 0, 7, а ДКК = 0). Однако объем вычислений для ЭКК несколько больше, чем для ДКК. В настоящее время для сбора и обработки эвристической информации применяют новые теории, например, теорию нечетких множеств. В работе [17] приводятся примеры использования возможностей, параметрическое представление управленческих оценок в виде нечетких интервалов, сравнение нечетких интервалов и др.
Контрольные вопросы и задания к разделу 1
1.1. 1. Эволюция ФСА. 2. В чем заключается универсальность метода ФСА? 3. Области применения ФСА. 4. Менеджмент качества и ФСА. 5. На чем базируется ФСА? Основная идея метода. 6. В чем отличие ФСА от традиционных методов анализа? 7. Трудности внедрения результатов ФСА.
1.2.
|

 (1)
(1) (2)
(2) (3)
(3)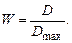 (4)
(4) (5)
(5) (6)
(6) (7)
(7) зависит только от n и m (числа объектов и количества экспертов). Осуществив ряд последовательных преобразований [9], можно получить
зависит только от n и m (числа объектов и количества экспертов). Осуществив ряд последовательных преобразований [9], можно получить
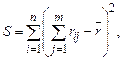 можно записать выражение для оценки D в виде
можно записать выражение для оценки D в виде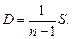
 (8)
(8)
 Здесь Тj – показатель связанных рангов в j -й ранжировке, Hj – число групп равных рангов в j -й ранжировке,
Здесь Тj – показатель связанных рангов в j -й ранжировке, Hj – число групп равных рангов в j -й ранжировке,  .
. степенями свободы.
степенями свободы.


 – ранги в первой и второй ранжировках соответственно;
– ранги в первой и второй ранжировках соответственно;  – оценки средних рангов.
– оценки средних рангов.
 преобразований, можно получить удобную для расчетов формулу КРК Спирмена для несвязанных рангов:
преобразований, можно получить удобную для расчетов формулу КРК Спирмена для несвязанных рангов:
 . Значение r = –1 имеет место при противоположных ранжировках (прямой и обратной). Если КРК=1, то ранжировки считаются линейно независимыми.
. Значение r = –1 имеет место при противоположных ранжировках (прямой и обратной). Если КРК=1, то ранжировки считаются линейно независимыми.

 табулированы [11].
табулированы [11].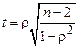 приближенно распределена по закону Стьюдента
приближенно распределена по закону Стьюдента 


 .
. .
. .
.

 – отношение количества экспертов mij, приписавших объекту О i ранг j, к общему числу объектов m.
– отношение количества экспертов mij, приписавших объекту О i ранг j, к общему числу объектов m. тогда
тогда  Подставив Рij в выражение для определения Н, получим:
Подставив Рij в выражение для определения Н, получим:



