Ожидаемая скорость скольжения, для рассматриваемого заданияVS ≈ 0, 45 ∙ 10-3∙ 750∙ С учетом указанных рекомендаций из прилагаемых табл. 5 [4] выбираем: для червяка – сталь 40Х, термообработка улучшение и закалка ТВЧ, твердость поверхности зубьев 45…50 НRC (420…500 НВ), σ Т = 750 Н/мм2; для зубчатого венца колеса – безоловянную бронзу марки БрА9ЖЗЛ, отливка в кокиль σ Т = 195 Н/мм2; σ В = 490 Н/мм2 (таблица 25 [4]). 2.3 Допускаемые контактные напряжения Допускаемые контактные напряжения для материалов I г р у п п ы определяются в следующей последовательности: определяется общее число циклов перемены напряжений N = 60n2 ∙ t, где t – ресурс работы редуктора, если по расчету N ≥ 25 ∙ 107, то принимают N = 25 ∙ 107; коэффициент долговечности КHL = коэффициент интенсивности изнашивания зубьев СV =1, 66VS-0, 352 или принимают в зависимости от скорости скольжения из следующего ряда:
Допускаемое контактное напряжение при числе циклов перемены напряжений, равном 107 [σ ]НО = (0, 75…9) σ В, где коэффициент 0, 75 для червяков принимают при НRС < 45, (НВ ≥ 350); 0, 9 при НRС ≥ 45 (НB> 350), а σ В принимают по табл. 5 [4]. С учетом указанной последовательности, допускаемые контактные напряжения определяются по итоговой формуле [σ ]Н = КHL∙ CV[σ ]НО. II г р у п п а. [σ ]НО = 250 Н/мм2 для червяков при НВ ≤ 350; [σ ]НО = 300 Н/мм2 для червяков при (НВ ≥ 350). Допускаемые контактные напряжения [σ ]Н = [σ ]НО – 25 VS = 300-25∙ 3, 32= 217 Н/мм2. III г р у п п а. Допускаемые контактные напряжения [σ ]Н = 175 – 35 VS.
2.4 Допускаемые изгибные напряжения Допускаемые изгибные напряжения определяются по следующей методике: определяется коэффициент долговечности КFL = где N – число циклов нагружения, рассчитывается исходное допускаемое напряжение изгиба по формулам: для материалов I и II групп: [σ ]Fo = 0, 25σ Т + 0, 08σ В; для материалов III группы: [σ ]Fo = 0, 12σ В ∙ и; определяется расчетное допускаемое напряжение изгиба [σ ]F = KFL∙ [σ ]Fo. Для рассматриваемого примера, для материалов, выбранных ранее в п.2.2, и в соответствии с предложенной методикой, определяются: N = 60∙ n2 t = 60∙ 25∙ 30000 = 4, 5∙ 107 = 45∙ 106 КFL = [σ ]Fo = 0, 25∙ 195 + 0, 08∙ 490=87, 95 Н/мм2, где значения σ Т = 195 Н/мм2 и σ В = 490 Н/мм2, определены ранее в п.2.2 [σ ]F = 0, 66∙ 87, 95 = 58, 05 H/мм2. Для дальнейших расчетов принимаем [σ ]Н = 217 Н/мм2 и [σ ]F = 58, 05 Н/мм2. 2.5 Проектировочный расчет На первом этапе проектировочного расчета из обеспечения условий прочности определяются основные геометрические параметры передачи.
2.5.1 Межосевое расстояние Межосевое расстояние определяется из условия контактной прочности зубьев по формуле aw ≥ 61 где а w – межосевое расстояние, 61 – цифровой коэффициент червячной передачи. Для рассматриваемого примера aw ≥ 61 Рассчитанное значение aw необходимо привести к ряду нормальных чисел, в соответствии с табл. 1 [4]. Стандартное значение межосевого расстояния aw = 170 мм. 2.5.2 Основные параметры передачи Число заходов червяка z1 зависит от передаточного числа u и определяется из следующего ряда чисел: 8 ≤ u ≤ 14 14 < u < 30 u ≥ 30 z1 = 4 z1 = 2 z1 = 1. Для рассматриваемого примера u =30, следовательно z1 = 1; число зубьев колеса z2 = u·z1; z2 = 30·1=30. Выполняться условие z2> zmί n = 28, чтобы не было подрезания зубьев. Предварительное значение модуля передачи определяется по выражению m = (1, 5…1, 7) где m1 – предварительное значение модуля передачи, m = (1, 5…1, 7) Полученное значение модуля округляют до стандартного значения модуля в соответствии с приведенным рядом стандартных модулей: m, мм 2, 5; 3, 15; 4; 5; 6, 3; 8; 10; 12, 5; 16. Из этого ряда выбираем стандартное значение модуля m = 10 мм. Предварительное значение коэффициента относительного диаметра червяка определяют по формуле: q = После подстановки в формулу рассчитанных цифровых значений получим q = Минимальное допускаемое значение q из условия жесткости червяка проверяют по условию qmin = 0, 212 · z2; qmin = 0, 212 · 30 = 6, 36, так как рассчитанное значение q = 4 меньше минимального допустимого qmin = 6, 36, то для дальнейших расчетов принимают большее значение q при рассчитанном модуле m = 10 мм из табл.29 [4], q = 8. Для принятия окончательного решения о правильности расчетов и выбора параметров аw, z2, q определяют коэффициент смещения х: х = при цифровой подстановке: х = 170/10 – 0, 5(30+8) = 17 - 19= - 2. Если по расчету | x | > 1, то изменяют значение а w, q илиz2 из соответствующего ряда стандартных значений. Принимаем а w= 180, тогда также m = 10 мм, q = 8. х = 180/10 – 0, 5(30+8) = 18-19 = -1. Так как значение | x | = 1, то принятые параметры аw, z2, q не изменяются и нарезание зубьев производится без смещения инструмента. Определяется значение фактического передаточного числа uф = z2/z1 и отклонение Δ u от заданного Δ u = В рассматриваемом случае Δ u = Следовательно, фактическое передаточное число соответствует заданному. 2.5.3 Геометрические размеры червяка и колеса Определяются по стандартным формулам, приведенным ниже: делительный диаметр червяка d1 = mq = 10· 8 = 80 мм; диаметр вершин витков червяка d a 1 = d1 +2m = 80+2· 10 = 100 мм; диаметр впадин df1 = d1 – 2, 4m = 80-2, 4· 10 = 56мм; длина нарезной части червяка при коэффициенте смещения x < 0 в 1 = (10+5, 5 | x | +z1) · m = (10 + 5, 5 |-1| + 1) · 10 = 165 мм. Полученное значение в 1 округляют в большую сторону до стандартного числа из табл. 1 [4], т.е. в 1 = 170 мм. Примечание. При положительном смещении, т.е. х > 0, червяк должен быть несколько короче. В этом случае размер в 1, рассчитанный по приведенной выше формуле, уменьшают на величину (70 +60 · х)· m/z2 и вновь полученное значение в 1 приводят к ряду стандартных чисел. диаметр делительной окружности колеса d2 = m·z2 = 10·30 = 300 мм; уточнение межосевого расстояния аw = 0, 5(d1+d2) = 0, 5· (80 + 300) = 190 мм; диаметр окружности вершин зубьев колеса d a 2 = d2 + 2(1 + x)· m = 300 + 2·10 = 320 мм. Примечание. При уточненном значении аw величина коэффициента смещения х 1 определяется по формуле х = диаметр колеса наибольший d a m2 ≤ d a2 +6m/(z1 + 2) = 320 + 6∙ 10/1 +2 = 340 мм; диаметр окружности впадин колеса df2 = d2 -2∙ m(1, 2 – x) = 300 - 2∙ 10∙ 1, 2 = 276 мм; ширина венца колеса в 2 = φ а · аw, где значение коэффициента φ а принимается равным 0, 355, если z1 = 1 и 2 и равно 0, 315, если z1 = 4, в 2 = 0, 355· 190 = 67, 45 мм., полученное значение в 2 округляют в ближайшую сторону по табл. 1 [4], в 2 = 71 мм; высота головки зуба h a = m = 10 мм; высота ножки зуба h f = 1, 2m = 1, 2·10 = 12 мм; высота зуба h = h a + hf = 10+12 = 22 мм; шаг зацепления Р = π · m = 3, 14· 10 = 31, 4 мм; толщина зуба S, равная ширине впадин е, т.е. S = e =0, 5· P = 0, 5· 31, 4 = 15, 7 мм; радиальный зазор С = 0, 2· m = 0, 2· 10 = 2 мм; угол наклона (подъема) линии витка червяка γ = arctg [z1 /(q + 2· x)] = arctg [1/8] = 7, 1250 (7007'). После проведения расчетов основных геометрических параметров червяка, колеса и передачи в целом, определяют конструктивную форму колеса и червяка.
2.5.4 КПД передачи КПД передачи рассматривается с целью определения доли потерь энергии, затраченной на нагрев составных деталей редуктора. КПД передачи определяется по формуле η = 0, 95 · где р' – приведенный угол трения между червяком и колесом, принимают в соответствии со следующим рядом:
Меньшее значение угла р' - для оловянной бронзы, большее значение – для безоловянной бронзы, латуни и чугуна. Для определения значения угла р' необходимо предварительно определить уточненную скорость скольжения в зацеплении: VSф = V1/cosγ, где V1 – окружная скорость на червяке (V1 = π d1n1/60000 м/с), а угол γ определен ранее в п.2.5.3. Окружная скорость на колесе определяется по формуле: V2 = π d2n2/60000 м/с. Для рассматриваемого примера: V1 = 3, 14· 80· 750/60000 = 3, 14 м/с; V2 = 3, 14· 300· 25/60000=0, 39м/с; VSф = 3, 14/cos70 07' = 3, 14/0, 992 = 3, 17 м/с. VSф = 3, 17 м/с отличается от предварительно принятой (смотри п.2.2) VS = 3, 32 м/с, поэтому [σ ]н = [σ ]но – 25Vs = 300 - 25· 3, 17 = 220, 75 Н/мм2. По найденному значению скорости VSф из представленного ряда углов р' определяем необходимое значение р' = 10 54'. Подставляя найденное значение р'= 70 07' в формулу для определения КПД, находим: η = 0, 95 Рассчитанное значение укладывается в интервал предварительно выбранных значений КПД. 2.5.5 Тепловой расчет передачи Червячный редуктор в связи с невысоким значением КПД и большим выделением теплоты проверяют на нагрев. Условие работы редуктора без перегрева определяется: tраб ≤ [tраб], где tраб – температура нагрева масла в 0С, которая не должна превышать для широко применяемых масел 950С. Температура нагрева масла без искусственного охлаждения: tраб = [(1 – η)Р1/КтА]+200С, где Р1 = π n2Т2/30η или Р1 = Т1ω 1 – мощность на валу-червяке Вт; Кт = 12…18 Вт/м2 С0 – коэффициент теплоотдачи; А – площадь поверхности охлаждения корпуса редуктора приближенно определяемая из прилагаемого ряда, как функция от аw:
После подстановки в указанные формулы, рассчитанных ранее значений, находим: при аw = 190 мм и А ≈ 0, 735 м2 мощность на входном валу Р1 = температура нагрева масла tраб = [(1 – 0, 75)· 339, 1/(12…18)0, 735]+ 200 ≈ 114…830С. Таким образом, условие работы редуктора без перегрева не соблюдается, поэтому необходимо улучшить условия охлаждения. Этого можно достичь двумя конструкторскими решениями: во-первых, увеличить поверхность охлаждения за счет создания ребер охлаждения на корпусе редуктора; во-вторых, предусмотреть установку вентилятора и обеспечить принудительную вентиляцию редуктора, в этом случае расчет температуры нагрева производится по формуле: tраб = [(1-η)Р1/(0, 7Кт +0, 3Ктв)· А]+ 200С, где Ктв – коэффициент теплоотдачи при обдуве вентилятором, выбирается в зависимости от числа оборотов вентилятора, который может быть установлен на входном валу редуктора, из следующего ряда:
Выбор способа улучшения охлаждения редуктора зависит от условий поставленной задачи. В рассматриваемом варианте решения задания приемлем любой способ, в частности при применении вентилятора температура нагрева масла определяется: tраб = Вывод. Обеспечение условий охлаждения редуктора достигается за счет установки вентилятора на входном валу редуктора и обеспечения хороших условий обдува (т.е. выбором большего значения коэффициента Кт). 2.5.6 Силы в зацеплении В червячном зацеплении действуют окружная, радиальная и осевая силы, которые рассчитываются по формулам (см. рис.3): окружная сила на колесе, равная осевой силе на червяке Ft2 = F a 1= 2T2/d2; окружная сила на червяке, равная осевой силе на колесе Ft1 = F a 2 = 2T2/(u · d1 · η); радиальная сила Fr1 = Fr2 =Ft2 · tgα, где α = 200 – стандартный угол зацепления; tg200 = 0, 3640.
Рис.3 Силы, действующие в червячном зацеплении В рассматриваемом примере Ft2 = F a 1= Ft1 = F a 2= Fr1 = Fr2 = 6361, 3· 0, 3640 = 2315, 5 Н.
2.5.7. Степень точности зацепления Степень точности зацепления передачи принимают по табл.20 [4] в зависимости от окружной скорости колеса. Окружная скорость колеса определена ранее в п.2.5.4, V2 = 0, 39 м/с и в соответствии с табл.20 [4] степень точности равна 9. 2.6. Проверочный расчет Проверочный расчет передачи на прочность производится по контактным напряжениям и по направлениям изгиба зубьев колеса. Червяки обычно выполняют за одно целое с валом, т.е. в виде вала-червяка, поэтому проверочный расчет на прочность и жесткость производится как для валов. 2.6.1. Проверочный расчет по контактным напряжениям Условие прочности σ н = (0, 9…1, 1) [σ н], σ н – расчетное (фактическое) контактное напряжение, определяется по формуле σ н = где Кн – коэффициент нагрузки, при V2 ≤ 3 м/с Кн =1, а при V2 > 3 м/с Кн = 1, 1…1, 3. Подставив в расчетную формулу исходные данные для рассматриваемого примера, имеем: σ н = Вывод. Условие контроля по контактным напряжениям выполняется, так как σ н = 174, 8 Н/мм2 меньше диапазона [σ н] = 220, 75…242, 8 Н/мм2. [σ н] определено в п.2.3 и уточнено в п.2.5.4. σ н = 174, 8 Н/мм2< [σ н]= =220, 75 Н/мм2. 2.6.2. Проверочный расчет по напряжениям изгиба зубьев Условие прочности σ F = где YF – коэффициент формы зуба, принимается из ряда в зависимости от эквивалентного числа зубьев колеса:
ZV2 = z2/cos3γ, а коэффициент К был определен ранее в п.2.6.1. Для рассматриваемого примера, из результатов ранее рассчитанных параметров следует: КF = Кн = 1, и ZV2 = 30/0, 9923 = 30, 73. Этому значению соответствует YF = 1, 71. Тогда σ F = Вывод. Условие прочности зубьев по напряжениям изгиба зубьев выполняется, так как σ F = 10, 72 Н/мм2 < < [σ ]F · 1, 1 = 58, 05 · 1, 1 = 63, 86 Н/мм2. Результаты расчета червячной передачи приведены в таблице 2 Таблица 2 Результаты расчета червячной передачи
Продолжение таблицы 2
3 Эскизное проектирование передачи Общие положения Эскизное проектирование передач включает: определение размеров валов; выбор подшипников и схемы их установки; эскизное конструирование валов и компоновку передач редуктора; расчеты валов на прочность. На рисунке 4 показана расчетная схема червячного редуктора для эскизного проектирования.
Рис.4 Расчетная схема редуктора для эскизного проектирования Основные конструктивные схемы валов и обозначений геометрических размеров показаны на рис. 3.1, 3.2, 10.6, 10.7, 10.8 [3], 4.2 [2], с.136. Валы следует конструировать по возможности гладкими, с минимальным числом уступов, что приводит к существенному сокращению расхода металла на изготовление. Для осевого фиксирования валов наиболее простой является схема установки подшипников «враспор». Входной и выходной валы редукторов имеют консольные цилиндрические или конические участки для установки полумуфт. Минимальные диаметры валов рассчитываются из условия только на кручение, как это было показано в сопротивлении материалов, по пониженным допускаемым касательным напряжениям [τ ] по формуле: d = где при [τ ] = 10…25 Н/мм2 коэффициент с = 6…8, вращающий момент Т в Н·м. 3.1 Проектировочный расчет входного вала и выбор подшипников 3.1.1 Расчетная схема. Исходные данные
Рис. 5 Расчетная схема входного вала Входной вал В1 имеет цилиндрический консольный участок длиной ℓ МБ и диаметром d, промежуточный участок длиной ℓ КБ для установки подшипников и уплотнений диаметром dп, участки диаметром буртика dБП для упора во внутренние кольца подшипников, средний участок, представляющий червяк диаметром вершин витков червяка d а 1 и длиной нарезанной части в 1. Участок ℓ МБ имеет наименьший диаметр, рассчитываемый из условия работы только на кручение, и служит для установки муфты Х1, соединяющей с валом электродвигателя. Исходные данные: Т1 = 45, 44 Н·м; аw = 190 мм; d а 1 = 100 мм; df = 56 мм; в 1 = 170 мм; d ам2 = 340 мм. 3.1.2 Геометрические размеры вала и выбор подшипников Определение наименьшего диаметра вала из условия его работы только на кручение d = Этот диаметр согласуется с диаметром вала электродвигателя по условию d= (0, 7…1, 0) dэ =(0, 7…1, 0) 42 = 29, 4…42 мм. Принимаем стандартное значение диаметр вала d = 30 мм (таблица 1 [4]).
|
3, 32 м/с.
;
,
≈ 0, 66
,
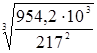= 166, 3 мм.
,
= 8, 5…9, 63 мм.
.
.
- 0, 5 (z2 + q),
.
.
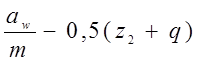равно нулю;
,
.
= 3329, 1 Вт;
С = 104…840С.
Н;
Н;
,
Н/мм2.
,
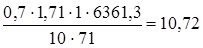Н/мм2.
,
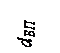
Расчетная схема входного вала приведена на рисунке 5.
= 22, 5мм.
