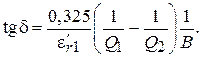При измерении скалярной диэлектрической проницаемости необходимо обеспечить отсутствие вырождения рабочего вида колебаний. В цилиндрическом резонаторе все виды колебаний с индексом  невырожденые. Для измерения сравнительно малых значений диэлектрической проницаемости используется вид колебаний
невырожденые. Для измерения сравнительно малых значений диэлектрической проницаемости используется вид колебаний  . При этом образец помещается на оси резонатора в максимуме электрического поля и оказывает существенное влияние на параметры резонатора. Задача определения диэлектрической проницаемости и угла потерь сводится к решению уравнений электромагнитного поля для цилиндрического резонатора и учету влияния на это поле исследуемого образца диэлектрика. Измеряемыми величинами являются резонансная частота
. При этом образец помещается на оси резонатора в максимуме электрического поля и оказывает существенное влияние на параметры резонатора. Задача определения диэлектрической проницаемости и угла потерь сводится к решению уравнений электромагнитного поля для цилиндрического резонатора и учету влияния на это поле исследуемого образца диэлектрика. Измеряемыми величинами являются резонансная частота  и добротность пустого резонатора
и добротность пустого резонатора  , резонансная частота
, резонансная частота  и добротность
и добротность  резонатора при введенном в резонатор исследуемом образце.
резонатора при введенном в резонатор исследуемом образце.
Из теории малых возмущений (см. прил. 1) известно, что
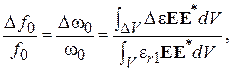
где  – изменение частоты при внесении диэлектрика;
– изменение частоты при внесении диэлектрика;  – отличие относительной диэлектрической проницаемости вносимого диэлектрика
– отличие относительной диэлектрической проницаемости вносимого диэлектрика 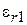 от проницаемости среды
от проницаемости среды  , заполняющей объем резонатора
, заполняющей объем резонатора  ;
;  – объем диэлектрика.
– объем диэлектрика.
Выражение для запасенной в резонаторе энергии имеет вид

Добротность пустого резонатора определяется известной формулой

где 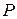 – мощность потерь в резонаторе. При внесении образца диэлектрика в резонатор его добротность изменяется за счет небольших изменений
– мощность потерь в резонаторе. При внесении образца диэлектрика в резонатор его добротность изменяется за счет небольших изменений  и
и 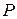 , так что добротность резонатора с образцом будет иметь вид:
, так что добротность резонатора с образцом будет иметь вид:

Используя выражения (1.18) и (1.19) и предполагая, что  и
и  , что справедливо, если объем внесенного диэлектрика значительно меньше объема резонатора, получим формулу изменения добротности резонатора
, что справедливо, если объем внесенного диэлектрика значительно меньше объема резонатора, получим формулу изменения добротности резонатора

где

– изменение мощности потерь за счет внесения диэлектрика.
В цилиндрическом резонаторе при использовании основного, наиболее низкочастотного, вида колебаний  (рис. 1.2) электрическое поле имеет только продольную компоненту:
(рис. 1.2) электрическое поле имеет только продольную компоненту:

где  – функция Бесселя нулевого порядка;
– функция Бесселя нулевого порядка;  – волновое число;
– волновое число; 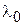 – длина; волны рассматриваемого вида колебания;
– длина; волны рассматриваемого вида колебания;  – расстояние от оси резонатора до точки наблюдения. В соответствии с (1.21) электрическое поле имеет в центре резонатора максимальную напряженность
– расстояние от оси резонатора до точки наблюдения. В соответствии с (1.21) электрическое поле имеет в центре резонатора максимальную напряженность  , определяемую подводимой от генератора мощностью, и принимает нулевое значение на стенке резонатора
, определяемую подводимой от генератора мощностью, и принимает нулевое значение на стенке резонатора  .
.
Поместив вдоль продольной оси такого резонатора образец диэлектрика в виде тонкого цилиндрического стержня радиуса  и высотой
и высотой 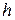 (рис. 1.2), считаем, что при выполнении условия
(рис. 1.2), считаем, что при выполнении условия

поле в образце остается однородным. Выполняя интегрирование числителя и знаменателя формулы, и используя соотношение  , получим следующие выражения:
, получим следующие выражения:

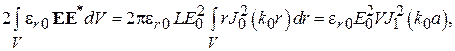
где 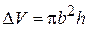 и
и  объемы внесенного образца диэлектрика и резонатора, соответственно. Для резонатора с воздушным заполнением
объемы внесенного образца диэлектрика и резонатора, соответственно. Для резонатора с воздушным заполнением  . Подставив значения интегралов и в формулу, учитывая, что
. Подставив значения интегралов и в формулу, учитывая, что  и решая полученное уравнение относительно
и решая полученное уравнение относительно  , найдем:
, найдем:

Формула позволяет определить диэлектрическую проницаемость образца по результатам измерений резонансных частот пустого резонатора  и резонатора с внесенным образцом
и резонатора с внесенным образцом  .
.
Если внесение исследуемого образца приводит к значительному изменению частоты, то существует возможность уменьшить это изменение, сместив образец в сторону от оси резонатора. Формула для диэлектрической проницаемости при смещении диэлектрика от продольной оси принимает вид:

где  – коэффициент уменьшения поля,
– коэффициент уменьшения поля,  – расстояние от оси резонатора до точки, в которой укреплен образец. При таких положениях образца возрастает погрешность измерения
– расстояние от оси резонатора до точки, в которой укреплен образец. При таких положениях образца возрастает погрешность измерения 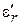 за счет ошибки определения коэффициента
за счет ошибки определения коэффициента  , которая возрастает при увеличении расстояния
, которая возрастает при увеличении расстояния  от оси
от оси  до оси образца.
до оси образца.
Другим способом уменьшения ухода частоты является уменьшение высоты образца. При исследовании образцов с  следует иметь в виду, что поле резонатора искажается тем больше, чем выше значение диэлектрической проницаемости образца. В этом случае теория малых возмущений, использованная при выводе формулы, оказывается неприменимой, что ограничивает возможность использования метода при исследовании диэлектриков с
следует иметь в виду, что поле резонатора искажается тем больше, чем выше значение диэлектрической проницаемости образца. В этом случае теория малых возмущений, использованная при выводе формулы, оказывается неприменимой, что ограничивает возможность использования метода при исследовании диэлектриков с  . Следует заметить, что наиболее точные результаты получаются при использовании образцов, длина которых равна высоте резонатора.
. Следует заметить, что наиболее точные результаты получаются при использовании образцов, длина которых равна высоте резонатора.
Уменьшение ухода частоты достигается также уменьшением радиуса образца, что, однако, сопряжено с трудностями изготовления измеряемого образца и увеличением погрешностей, обусловленных качеством обработки образца.
Для получения формулы, связывающей параметры цилиндрического резонатора с тангенсом угла потерь исследуемого диэлектрика  , воспользуемся выражением. Потери в цилиндрическом образце, расположенном по оси резонатора, могут быть представлены в виде:
, воспользуемся выражением. Потери в цилиндрическом образце, расположенном по оси резонатора, могут быть представлены в виде:

Используя выражение для энергии, запасенной в резонаторе, получим формулу для тангенса потерь  :
:

Полученная формула для  позволяет определить угол потерь исследуемых диэлектриков по измеренным значениям добротности резонатора без образца
позволяет определить угол потерь исследуемых диэлектриков по измеренным значениям добротности резонатора без образца 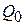 и добротности с образцом
и добротности с образцом  . Использование этой формулы допустимо для материалов с
. Использование этой формулы допустимо для материалов с 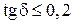 . При более высоких потерях в образце резонансная кривая резонатора с образцом сильно «расплывается» и сам метод малых возмущений перестает быть справедливым.
. При более высоких потерях в образце резонансная кривая резонатора с образцом сильно «расплывается» и сам метод малых возмущений перестает быть справедливым.
Точность измерения диэлектрической проницаемости зависит от погрешностей измерений всех величин, входящих в расчетную формулу, и может быть приблизительно оценена в 2…3 %, а точность определения  – порядка 10 %. При этом основная ошибка вносится неточностью определения диаметра образца и добротности резонатора.
– порядка 10 %. При этом основная ошибка вносится неточностью определения диаметра образца и добротности резонатора.
Цилиндрические резонаторы с колебаниями типа  не позволяют исследовать материалы с высокими значениями проницаемости и потерь, так как требуемое для исследований расположение образца в максимуме электрического поля приводит к значительным изменениям параметров резонатора. Например, на длине волны 1 см максимальный радиус образца с
не позволяют исследовать материалы с высокими значениями проницаемости и потерь, так как требуемое для исследований расположение образца в максимуме электрического поля приводит к значительным изменениям параметров резонатора. Например, на длине волны 1 см максимальный радиус образца с  не должен превышать 0, 1 мм, что практически невыполнимо, учитывая необходимую точность изготовления образца.
не должен превышать 0, 1 мм, что практически невыполнимо, учитывая необходимую точность изготовления образца.
Применение цилиндрических резонаторов с колебаниями типа

позволяет исследовать образцы со сравнительно высокими потерями

и значительно большего диаметра без опасности существенного возмущения поля. На рис. 1.3 изображено распределение полей в цилиндрическом резонаторе, возбужденном на волне типа

, с образцом внутри. Единственная составляющая электрического поля

для этого типа колебаний может быть записана в виде

где 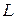 – высота резонатора;
– высота резонатора;  – значение первого корня функции Бесселя первого рода первого порядка. Вблизи оси резонатора электрическое поле близко к нулю, поэтому его возмущение образцом невелико.
– значение первого корня функции Бесселя первого рода первого порядка. Вблизи оси резонатора электрическое поле близко к нулю, поэтому его возмущение образцом невелико.
Проводя интегрирование числителя и знаменателя уравнения для измененной частоты при внесенном диэлектрическом образце и применяя рекуррентную формулу
 ,
,
получаем формулу для диэлектрической проницаемости цилиндрического образца, ось которого совпадает с продольной осью резонатора:

где
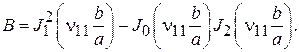
Формулу для вычисления  исследуемого материала можно получить, используя соотношения, и. При внесении образца в резонатор изменяется мощность потерь в резонаторе и величину этого изменения можно записать следующим образом:
исследуемого материала можно получить, используя соотношения, и. При внесении образца в резонатор изменяется мощность потерь в резонаторе и величину этого изменения можно записать следующим образом:
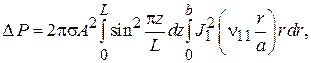
Энергия, запасенная в резонаторе, определяется следующим выражением:

Подставляя полученные выражения для  и
и 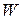 в формулу и используя числовой коэффициент
в формулу и используя числовой коэффициент  из, после необходимых преобразований получим:
из, после необходимых преобразований получим:
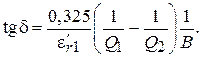
Последнее выражение позволяет получить формулу, связывающую параметры цилиндрического резонатора с тангенсом угла потерь исследуемого диэлектрика.
 – изменение мощности потерь за счет внесения диэлектрика.
– изменение мощности потерь за счет внесения диэлектрика.
 позволяет исследовать образцы со сравнительно высокими потерями
позволяет исследовать образцы со сравнительно высокими потерями  и значительно большего диаметра без опасности существенного возмущения поля. На рис. 1.3 изображено распределение полей в цилиндрическом резонаторе, возбужденном на волне типа
и значительно большего диаметра без опасности существенного возмущения поля. На рис. 1.3 изображено распределение полей в цилиндрическом резонаторе, возбужденном на волне типа  , с образцом внутри. Единственная составляющая электрического поля
, с образцом внутри. Единственная составляющая электрического поля  для этого типа колебаний может быть записана в виде
для этого типа колебаний может быть записана в виде

 невырожденые. Для измерения сравнительно малых значений диэлектрической проницаемости используется вид колебаний
невырожденые. Для измерения сравнительно малых значений диэлектрической проницаемости используется вид колебаний  . При этом образец помещается на оси резонатора в максимуме электрического поля и оказывает существенное влияние на параметры резонатора. Задача определения диэлектрической проницаемости и угла потерь сводится к решению уравнений электромагнитного поля для цилиндрического резонатора и учету влияния на это поле исследуемого образца диэлектрика. Измеряемыми величинами являются резонансная частота
. При этом образец помещается на оси резонатора в максимуме электрического поля и оказывает существенное влияние на параметры резонатора. Задача определения диэлектрической проницаемости и угла потерь сводится к решению уравнений электромагнитного поля для цилиндрического резонатора и учету влияния на это поле исследуемого образца диэлектрика. Измеряемыми величинами являются резонансная частота  и добротность пустого резонатора
и добротность пустого резонатора  , резонансная частота
, резонансная частота  и добротность
и добротность  резонатора при введенном в резонатор исследуемом образце.
резонатора при введенном в резонатор исследуемом образце.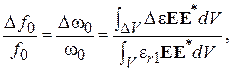
 – изменение частоты при внесении диэлектрика;
– изменение частоты при внесении диэлектрика;  – отличие относительной диэлектрической проницаемости вносимого диэлектрика
– отличие относительной диэлектрической проницаемости вносимого диэлектрика 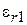 от проницаемости среды
от проницаемости среды  , заполняющей объем резонатора
, заполняющей объем резонатора  ;
;  – объем диэлектрика.
– объем диэлектрика.

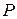 – мощность потерь в резонаторе. При внесении образца диэлектрика в резонатор его добротность изменяется за счет небольших изменений
– мощность потерь в резонаторе. При внесении образца диэлектрика в резонатор его добротность изменяется за счет небольших изменений  и
и 
 и
и  , что справедливо, если объем внесенного диэлектрика значительно меньше объема резонатора, получим формулу изменения добротности резонатора
, что справедливо, если объем внесенного диэлектрика значительно меньше объема резонатора, получим формулу изменения добротности резонатора


 – функция Бесселя нулевого порядка;
– функция Бесселя нулевого порядка;  – волновое число;
– волновое число; 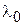 – длина; волны рассматриваемого вида колебания;
– длина; волны рассматриваемого вида колебания;  – расстояние от оси резонатора до точки наблюдения. В соответствии с (1.21) электрическое поле имеет в центре резонатора максимальную напряженность
– расстояние от оси резонатора до точки наблюдения. В соответствии с (1.21) электрическое поле имеет в центре резонатора максимальную напряженность  , определяемую подводимой от генератора мощностью, и принимает нулевое значение на стенке резонатора
, определяемую подводимой от генератора мощностью, и принимает нулевое значение на стенке резонатора  .
. и высотой
и высотой 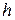 (рис. 1.2), считаем, что при выполнении условия
(рис. 1.2), считаем, что при выполнении условия
 , получим следующие выражения:
, получим следующие выражения:
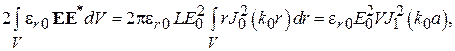
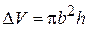 и
и  объемы внесенного образца диэлектрика и резонатора, соответственно. Для резонатора с воздушным заполнением
объемы внесенного образца диэлектрика и резонатора, соответственно. Для резонатора с воздушным заполнением  . Подставив значения интегралов и в формулу, учитывая, что
. Подставив значения интегралов и в формулу, учитывая, что  и решая полученное уравнение относительно
и решая полученное уравнение относительно  , найдем:
, найдем:

 – коэффициент уменьшения поля,
– коэффициент уменьшения поля, 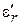 за счет ошибки определения коэффициента
за счет ошибки определения коэффициента  , которая возрастает при увеличении расстояния
, которая возрастает при увеличении расстояния  до оси образца.
до оси образца. следует иметь в виду, что поле резонатора искажается тем больше, чем выше значение диэлектрической проницаемости образца. В этом случае теория малых возмущений, использованная при выводе формулы, оказывается неприменимой, что ограничивает возможность использования метода при исследовании диэлектриков с
следует иметь в виду, что поле резонатора искажается тем больше, чем выше значение диэлектрической проницаемости образца. В этом случае теория малых возмущений, использованная при выводе формулы, оказывается неприменимой, что ограничивает возможность использования метода при исследовании диэлектриков с  . Следует заметить, что наиболее точные результаты получаются при использовании образцов, длина которых равна высоте резонатора.
. Следует заметить, что наиболее точные результаты получаются при использовании образцов, длина которых равна высоте резонатора. , воспользуемся выражением. Потери в цилиндрическом образце, расположенном по оси резонатора, могут быть представлены в виде:
, воспользуемся выражением. Потери в цилиндрическом образце, расположенном по оси резонатора, могут быть представлены в виде:
 :
:
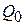 и добротности с образцом
и добротности с образцом  . Использование этой формулы допустимо для материалов с
. Использование этой формулы допустимо для материалов с 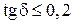 . При более высоких потерях в образце резонансная кривая резонатора с образцом сильно «расплывается» и сам метод малых возмущений перестает быть справедливым.
. При более высоких потерях в образце резонансная кривая резонатора с образцом сильно «расплывается» и сам метод малых возмущений перестает быть справедливым. не должен превышать 0, 1 мм, что практически невыполнимо, учитывая необходимую точность изготовления образца.
не должен превышать 0, 1 мм, что практически невыполнимо, учитывая необходимую точность изготовления образца.

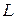 – высота резонатора;
– высота резонатора;  – значение первого корня функции Бесселя первого рода первого порядка. Вблизи оси резонатора электрическое поле близко к нулю, поэтому его возмущение образцом невелико.
– значение первого корня функции Бесселя первого рода первого порядка. Вблизи оси резонатора электрическое поле близко к нулю, поэтому его возмущение образцом невелико. ,
,
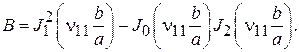
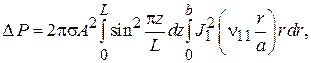

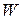 в формулу и используя числовой коэффициент
в формулу и используя числовой коэффициент  из, после необходимых преобразований получим:
из, после необходимых преобразований получим: