Рассмотрим слой, который имеет во всех точках одинаковую толщину Н и характеризуется некоторыми эквивалентными значениями удельной объемной проводимости  и относительной диэлектрической проницаемости
и относительной диэлектрической проницаемости 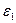 .
.
Постоянная времени разрядки слоя
 (3.36)
(3.36)
Время нарастания слоя на электроде
 (3.37)
(3.37)
где Со - скорость роста слоя.
 (3.38)
(3.38)
где v =  - скорость аэрозольной частицы у поверхности слоя; В — подвижность частицы; ЕК — напряженность поля коронного разряда у осадительного электрода; N — средняя концентрация частиц у поверхности слоя; Vср - средний объем частицы.
- скорость аэрозольной частицы у поверхности слоя; В — подвижность частицы; ЕК — напряженность поля коронного разряда у осадительного электрода; N — средняя концентрация частиц у поверхности слоя; Vср - средний объем частицы.
Если сопротивление слоя велико, т.е. постоянная времени нарастания слоя  » Tсл, то заряд не успевает уйти на электрод, и слой оказывается равномерно заряженным с плотностью объемного заряда р.
» Tсл, то заряд не успевает уйти на электрод, и слой оказывается равномерно заряженным с плотностью объемного заряда р.
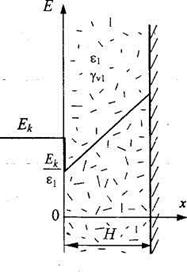
В этом случае напряженность поля внутри слоя будет равна
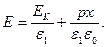 (3.39)
(3.39)
И максимальная напряженность поля будет на поверхности электрода:
 (3.40)
(3.40)
где  = рН - плотность заряда слоя на единицу поверхности электрода.
= рН - плотность заряда слоя на единицу поверхности электрода.
Если же слой так медленно растет, что заряд слоя успевает стечь ( «Tсл,), то весь заряд находится на поверхности слоя, и процесс зарядки поверхности слоя будет аналогичен зарядке отдельной лежащей на электроде частицы. Тогда все определяется соотношением проводимости в поле коронного разряда и слоя частиц. На поверхности слоя накопится свободный заряд:
«Tсл,), то весь заряд находится на поверхности слоя, и процесс зарядки поверхности слоя будет аналогичен зарядке отдельной лежащей на электроде частицы. Тогда все определяется соотношением проводимости в поле коронного разряда и слоя частиц. На поверхности слоя накопится свободный заряд:
своб.уст
 (3.41)
(3.41)

 и относительной диэлектрической проницаемости
и относительной диэлектрической проницаемости 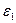 .
.
 (3.36)
(3.36) (3.37)
(3.37) (3.38)
(3.38) - скорость аэрозольной частицы у поверхности слоя; В — подвижность частицы; ЕК — напряженность поля коронного разряда у осадительного электрода; N — средняя концентрация частиц у поверхности слоя; Vср - средний объем частицы.
- скорость аэрозольной частицы у поверхности слоя; В — подвижность частицы; ЕК — напряженность поля коронного разряда у осадительного электрода; N — средняя концентрация частиц у поверхности слоя; Vср - средний объем частицы. » Tсл, то заряд не успевает уйти на электрод, и слой оказывается равномерно заряженным с плотностью объемного заряда р.
» Tсл, то заряд не успевает уйти на электрод, и слой оказывается равномерно заряженным с плотностью объемного заряда р.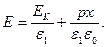 (3.39)
(3.39) (3.40)
(3.40) = рН - плотность заряда слоя на единицу поверхности электрода.
= рН - плотность заряда слоя на единицу поверхности электрода. (3.41)
(3.41)


