Примеры задач для самостоятельного решения
1. Если землевладелец, получающий со своего участка земли в 10 га арендную плату 25000 лир в год, решит продать его, то цена при ставке банковского процента 5% составит а) 25 000; б) 125 000; в) 50 000; г) 500 000. Решение: цена земли рассчитывается по формуле: Р = R/i = 25000/0, 05 = 500 000. Ответ: цена земли составит 500 000 лир.
2. Спрос на землю описывается уравнением: Q = 100 – 2R. Какова будет ставка ренты, если площадь земельных угодий составляет 90га? Какова будет цена одного гектара земли, если ставка банковского процента составляет 120 %? Государство устанавливает максимальный уровень ренты в 3 млн. Руб. За гектар. Как эта мера отразится на благосостоянии общества? Решение: равновесный уровень ренты определим из условия: 100 - 2R = 90, откуда R = 5. Цену одного гектара земли найдем по формуле: Р = R/i = 5/1, 2 = 4, 166 млн. руб. Если государство установит фиксированный уровень ренты, то объем спроса (100 – 6 = 94) превысит объем предложения земли. Величина земельной ренты, получаемой собственниками земли, сократиться с 90*5 = 450 до 90*3 = 270 млн. руб. Влияние данного решения на выигрыш покупателя земли оценить количественно невозможно: с одной стороны, они выигрывают от снижения уровня ренты, с другой стороны, проигрывают от дефицита земли. 3. Фермер выращивает пшеницу и продает ее на конкурентном рынке по 4 долл. за бушель. В краткосрочном периоде зависимость объема производства пшеницы от площади используемой земли (производственная функция) описывается формулой: Q = 2000X – 3X2, где Х – объем использования земли в гектарах. Сколько пшеницы будет ежегодно выращивать фермер, если рента, которую он платит за землю, составляет 320 долл. за гектар? Решение: найдем предельный продукт (МР) как производную по функции валового выпуска продукции (Q): 2000 – 6Х. Далее найдем предельный денежный продукт: МRP = МР*Р = 4(2000 – 6Х) = 8000 – 24Х. Предельный денежный продукт можно рассматривать в качестве рентного дохода: МRP = R, откуда: 320 = 8000 – 24Х. Соответственно Х = 320, а Q = 2000*320 – 3*3202 = 332 800. Ответ: 332 800 бушелей пшеницы будет ежегодно выращивать фермер. 4. Если по корпоративной облигации выплачивается доход в первый год в размере 1000 рублей, во второй год – 1200 рублей, а в третий – 1300 рублей, то при ставке банковского процента 10% какова будет дисконтированная стоимость этого потока доходов? Решение: воспользуемся формулой: Ответ: дисконтированная стоимость будет 2878, 26.
5. Номинальная процентная ставка – 12%, а уровень инфляции – 8%. Какова реальная ставка процента? Решение: воспользуемся формулой: Ответ: реальная ставка процента составляет 3, 6%.
6. Производственная функция фирмы в краткосрочном периоде: Q = 300L – L2, где L - объем использования труда, человеко – часы в неделю. Фирма реализует продукцию на конкурентном рынке по цене 0, 5 долл. за единицу. На рынке труда фирма выступает монопсонией, а функция предложения труда имеет вид: L = 2РL – 160, где РL – цена труда в долларах в неделю. Найдите оптимальный объем использования труда фирмой и цену труда, которую она установит. Решение: найдем функцию предельного продукта как производную по функции валового продукта: МР = 300 - 2L. Далее найдем функцию предельного денежного продукта: МRP = MP*P = (300 - 2L)*0, 5 = 150 – L. Перепишем функцию предложения труда: РL = 80 + 0, 5L. Найдем общие затраты фирмы на оплату труда: ТRС = Р*L = (80 + 0, 5L)*L = 80L – 0, 5 L2. Возьмем производную по функции общих затрат и найдем предельные расходы на ресурс: МRС = 80 + L. Приравняем МRP и МRС и найдем оптимальный объем использования труда для монополии: 150 – L = 80 + L, откуда L = 35. Воспользуемся функцией: РL = 80 + 0, 5L, и найдем цену труда: РL = 80 + 0, 5*35 = 97, 5. Ответ: оптимальный объем использования труда фирмой 35, а цена труда 97, 5.
|

 = 1000/1, 1 + 1200/1, 21 + 1300/1, 33 = 2878, 26.
= 1000/1, 1 + 1200/1, 21 + 1300/1, 33 = 2878, 26.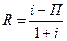 = (0, 12 – 0, 08)/(1 + 0, 12) = 0, 0357, или 3, 6%.
= (0, 12 – 0, 08)/(1 + 0, 12) = 0, 0357, или 3, 6%.


