Модель целенаправленной системы с управлением
Модель целенаправленной системы с управлением показана на рис. 3.2. Цель системы можно определить как задачу получения желаемого выходного результата или достижения желаемого состояния системы. Функционирование целенаправленной системы, определяемое протекающими в ней процессами изменения её состояний, направлено на достижение поставленных заранее (запланированных) целей.
x+ x‑
Рис. 3.2. Модель целенаправленной системы с компонентой управления в контуре обратной связи Общую цель системы называют глобальной или стратегической, поскольку её достижение планируется за длительный промежуток времени, обычно, ‑ несколько лет. Глобальная цель, как правило, имеет сложное строение, т.е. может быть подвергнута иерархической декомпозиции (разложению) на более простые локальные цели. При модульном строении системы локальные цели выступают как требования к выходам (выходным характеристикам) отдельных модулей системы. Именно продуманные требования на выходы согласовывают модули так, что состоящая из них система выполняет глобальную цель. Таким образом, локальные цели выступают важным регулятором организации частей и элементов в целенаправленную систему, а их согласование направляет проводимые в системе изменения в единое русло. Целенаправленное вмешательство в процесс функционирования системы называется управлением. Управление — важнейший инструмент достижения системных целей. Оно естественным образом связано с постановкой целей: именно возможность вмешательства, выбора, альтернативы делает процесс функционирования системы вариативным, а один или более из этих вариантов ‑ ведущим к достижению поставленной цели. Любой элемент обладает рядом свойств (параметров, характеристик), которые могут меняться в процессе функционирования системы. Вследствие этого могут измениться свойства, характеристики группы элементов (компонента, модуля) и всей системы в целом. Если зафиксировать все значения характеристик системы, важных для целей исследования или проектирования, то такую ситуацию называют состоянием системы. Процессом называют упорядоченный во времени набор состояний системы, соответствующий непрерывному или дискретному изменению (обычно – во времени) некоторого параметра, определяющего характеристики (свойства) системы. Для символьной записи процесса введем многомерную (по числу интересующих нас характеристик системы) величину у, описывающую конкретные значения этих характеристик. Все множество возможных величин обозначим через Y: y Î Y. Введем параметр процесса t, множество его значений Т и опишем у как функцию от этого параметра: y = y(t). Тогда процесс
Этому же процессу будет соответствовать отображение множеств T × Y®Y. Процессы в системе могут играть различную роль. Так, в системе автоматизированного проектирования процесс проектирования как движение от технического задания до рабочих чертежей является основной функцией системы. И, в целом, функционирование (а также создание) сложной системы обычно является процессом. Однако в том же проектировании необходимо учитывать целый ряд внутренних процессов: если что-то двигается, то ‑ уравнения движения, если идут химические превращения, то ‑ ход реакции. Таким образом, типичен учет процессов в системе как способ получения зависимостей выходов от входов в модулях разных иерархических уровней. При этом, в принципе, неважно, способствует ли в целом данный процесс выполнению системой ее функции или препятствует этому. К последнему случаю относятся, например, процессы износа, старения, а также действия противоположной стороны в игровых ситуациях. Общий вид процесса
Этому управляемому процессу будет соответствовать отображение множеств U× T× Y®Y. В (3.6) отражена лишь управляемость, вариативность процесса, но не его цель. Для записи процесса, приводящего к выполнению цели, начнем с того, что введем специальное обозначение f для тех выходных воздействий, на которые можно влиять выбором управлений и. Таким образом величины f, обычно называемые критериями, есть часть выходов x‑ рассматриваемого нами компонента или системы в целом (рис 3.1). Обозначим теперь желаемый вид выходных воздействий через fG, где G есть символ поставленной цели (от англ. GOAL – цель). Критерии f, естественно, считаем зависящими от характеристик (параметров) у: f=f (y). Пусть существует момент времени tG (или он задан) и существует состояние характеристик уG, позволяющие достичь цели fG. Пусть состояние уG может быть достигнуто управляемым процессом
Если в качестве критерия достижения цели рассматривать сам параметр y (т.е. если f(y)=y, то мы имеем в качестве цели желаемое состояние системы, так что надобность во втором равенстве в (3.7) отпадает, и управляемый процесс можно записать как Теперь можно сделать важное расширение формальной записи модели (3.4) – включением в нее параметра управления u. Рассмотрим управляемый процесс (правило перехода) Su. Пусть правило Su позволяет, с помощью выбора управления и из некоторой фиксированной совокупности U, достигать значения параметра состояния yG (т.е. целевого состояния). Параметр yG, в свою очередь, обеспечивает получение управляемых выходных воздействий f в виде fG, соответствующем достижению цели G (см. также (3.7)). Тогда кортежная запись модели управляемой системы получит следующий вид: S u: { x+, x-, fG, a, u, t, y Su, V, Модель оптимального планирования доставки товаров потребителям Задача оптимизации доставки товаров потребителям (скажем с нескольких складов в несколько магазинов) относится к классу задач оптимального планирования. Постановка задачи. Рассмотрим задачу нахождения такого плана перевозок продукции с М складов к N потребителям, который требовал бы минимальных затрат. Обозначим Хij. — количество продукции, поставляемое со склада i потребителю j. Пусть Pij — издержки доставки единицы продукции со склада i потребителю j. Предполагается, что транспортные расходы пропорциональны количеству перевозимой продукции, т. е. Q = РХ. Обозначим
С i— количество продукции, находящееся на складе i; Bj — количество продукции, необходимой потребителю j. Для решения задачи необходимо соблюдение следующего условия:
То есть, потребность в продукции всех потребителей должна быть обеспечена количеством товара на всех складах. Целевая функция определяется равенством
Исходными данными при решении данной задачи являются: · издержки транспортировки либо прибыль от реализации товара (массив Р); · количество товара на каждом складе (массив C); · количество товара, нужного каждому потребителю (масив В). Математическая модель задачи оптимального планирования формулируется следующим образом. Необходимо найти значения действительных переменных X 1, X 2..., Х n, для которых целевая функция Q (x) = P 1 X 1+ Р 2 Х 2 +... + Р n Х n принимает экстремальное (минимальное) значение на множестве точек, координаты которых удовлетворяют условиям: a 11 X 1 + a 12X2+... + a 1NXN = b 1 (3.11) а 21 Х 1 + а 22 Х 2 +... + а 2N Х N = b 2, … a M1 Х 1 + а M2Х2 +... + а MN X N = b M, Х 1≥ 0, Х 2≥ 0,..., X N≥ 0. Здесь коэффициенты aij, b i, P j (i = 1, 2,..., М; j = 1, 2,..., N) — действительные числа. Использование матричных обозначений позволяет записать задачу линейного программирования в виде: АХ = В, Х ³ 0, Q min(X) = PX, (3.12) где: X = (Х 1, Х 2,..., Х N)T, (T – операция трансформации матрицы) А ‑ матрица (а ij) размера M ´ N, Р = (Р 1, Р 2,..., Р N) ‑ вектор размера N, В = (b 1, b 2,..., b M)T ³ 0 ‑ вектор размера М, Q min(X) означает поиск минимума целевой функции. Q max(X) = РХ означает поиск максимума целевой функции. Очевидно соотношение: Q min(X) = ‑ Q max(X) (3.13) Точка X, удовлетворяющая всем условиям, называется допустимой точкой. Множество всех допустимых точек называется допустимой областью. Если после отбрасывания одного условия допустимая область не изменяется, то это условие считается лишним. В случае недостающего условия или для преобразования неравенства в равенство вводится дополнительная переменная. Решение подобных задач проводится методами линейного программирования. Линейным программированием называется раздел математики, в котором изучаются методы нахождения минимума или максимума линейной функции конечного числа переменных при условии, что они удовлетворяют конечному числу дополнительных условий, имеющих вид линейных уравнений или неравенств. Задачи подобной оптимизации решаются, например, программой Solver (Поиск решения) в табличном процессоре Microsoft Excel, которая относится к группе средств, выполняющих так называемый анализ " что-если". Суть этой методики состоит в том, что можно автоматически изменять исходные переменные задачи и сразу же видеть результаты этих изменений. Автоматическое обновление вычислений обеспечивает интерактивную обратную связь с экспериментами " что-если". Если для модели установлен автоматический пересчёт, то можно изменять (небольшими порциями - инкрементами) значение ячейки (или нескольких ячеек) независимой переменной (или нескольких переменных) и тут же увидеть результаты пересчёта во всех результирующих ячейках, которые зависят от изменённых значений. Программа запускаемая командой Поиск решения (Solver), может применяться для решения задач, которые включают много изменяемых ячеек (независимых переменных), и помогают найти такие их комбинации, которые минимизируют или максимизируют значения в целевых ячейках (зависимых переменных), которые содержат результаты вычислений, т.е. решений задачи оптимизации.
|


 есть некоторое правило перехода от ситуации со значением параметра t 0 к ситуации со значением t> t0 через все его промежуточные непрерывные или дискретные значения:
есть некоторое правило перехода от ситуации со значением параметра t 0 к ситуации со значением t> t0 через все его промежуточные непрерывные или дискретные значения:
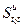 с управлением и из некоторой возможной совокупности управлений U выглядит так (сравните с (3.5)):
с управлением и из некоторой возможной совокупности управлений U выглядит так (сравните с (3.5)):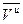 }
}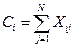 для i = 1, …, M
для i = 1, …, M  для j = 1, …, N
для j = 1, …, N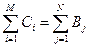 (3.9)
(3.9)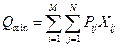 (3.10)
(3.10)


