Модель целенаправленной системы
Используя теоретико-множественные представления, модель самой абстрактной системы можно записать в виде кортежа (последовательности) двух множеств: S º < A, R > (3.1) где A = { ai } – множество элементов, а R = { rj } – множество связей (отношений) между элементами. Если известно, что элементы множества неоднородны, то это можно учесть в определении, добавляя в кортеж разные (под-) множества элементов: S º < A, B, R > где B = { bk } – множество элементов другого типа (отличного от A). В общем случае системный кортеж можно расширять за счёт добавления следующих множеств: QA – множество свойств элементов (ai ' A), QR – множество свойств связей (qj ' R), Z – цель, множество или структура целей системы, SR – среда, в которой существует (функционирует) целеустремлённая система, D T – период времени, в течение которого существует целеустремлённая система, N – наблюдатель, т. е. лицо, представляющее объект или процесс в виде системы при их исследовании или принятии решения, LN – язык, который наблюдатель использует для представления системы. В результате будет построена расширенная модель целенаправленной системы: S º < A, QA, R, QR, Z, SR, D T, N, LN > (3.2) Взгляд на определение системы как на средство ее исследования и создания позволил ввести определение, в котором система не расчленяется на элементы, т.е. не разрушается, что делается в вышеприведенном определении, а представляется как совокупность укрупненных компонент, принципиально необходимых для её существования и функционирования: S º < { Z }, { STR }, { TECH }, { COND }> (3.3) где Z = {z} - совокупность или структура целей; STR = {STR пр, STR орг,... } - совокупность структур, реализующих цели; STR np - производственная, STR орг, - организационная и т. п. ТЕСН - { meth, means, alg,... } - совокупность технологий (методы meth, средства means, алгоритмы alg и т.п.), реализаующих систему; COND - {j ex, j in } - условия существования системы, т.е. факторы, влияющие на ее создание и функционирование (jex‑ внешние, jin – внутренние). Такое определение особенно полезно для информационных систем автоматизированного управления. 3.3.2. Модель абстрактной системы с неопределённой структурой
x+ x‑
Рис. 3.1. Модель абстрактной системы с неизвестной структурой («чёрный ящик») Обозначим: - набор входных воздействий (входов) в системе х+ и всю их допустимую совокупность Х+, х+ Î Х+; - набор выходных воздействий (выходов) в системе х‑ и всю их возможную совокупность Х ‑ , х‑ Î Х ‑ ; - набор параметров, характеризующих свойства системы, постоянные во все время рассмотрения, и влияющих на выходные воздействия системы а и всю их допустимую совокупность А, а Î A; - набор параметров, характеризующих свойства системы, изменяющиеся во время ее рассмотрения (параметры состояния), у и всю их допустимую совокупность Y, y Î Y; - параметр (или параметры) процесса в системе t и всю их допустимую совокупность Т, t Î T; - правило S (функция, оператор) определения параметров состояния системы по входам х+, постоянным параметрам а и параметру процесса t. Заметим, что всегда следует различать величины и правило их определения. Так запись y=S(x+, a, t) означает нахождение параметров по этому правилу, в то время как о величине у можно говорить и вне правила ее определения; - правило V (функция, оператор) определения выходных характеристик системы по входам х+, постоянным параметрам а, параметру процесса t и параметрам состояния у, т. е. х‑ = V(x+, a, t, y); - правило На основе введения вышеуказанных воздействий, параметров и правил модель «чёрного ящика» может быть записана как кортеж S = < x+, x‑ , a, t, y, S, V,
|

 Здесь рассматривается модель системы с неопределенной структурой, т.е. системы элементы и связи которой не определены, [4]. Такая система представляется моделью «чёрного ящика», на вход которого подаются входные воздействия, и по определённому набору заранее известных свойств (параметров) системы исследуется её реакция на входные воздействия (рис. 3.1).
Здесь рассматривается модель системы с неопределенной структурой, т.е. системы элементы и связи которой не определены, [4]. Такая система представляется моделью «чёрного ящика», на вход которого подаются входные воздействия, и по определённому набору заранее известных свойств (параметров) системы исследуется её реакция на входные воздействия (рис. 3.1).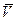 (функция, оператор) определения выходных характеристик системы по входам х +, постоянным параметрам а и параметру процесса. Указанное правило
(функция, оператор) определения выходных характеристик системы по входам х +, постоянным параметрам а и параметру процесса. Указанное правило 


