II. Нормальный закон распределения
Результаты, полученные при измерении той или иной величины, нельзя принять из-за ряда случайностей за достоверные (действительные значения измеряемых величин). Тогда приходится говорить о вероятности того или иного значения этих величин и определить их. Вероятность события - это количественная оценка объективной возможности появления данного события. Вероятность достоверных событий равна 1. Например, после ночи наступит утро. Вероятность невозможных событий равна 0. Случайные события имеют вероятность (p) больше 0, но меньше 1, т.е. 0 £ p £ 1. Если число всех равновероятных событий n и появление желательного результата возможно m раз, то p* = m/n (частота появления события). Как было показано Я. Бернулли, частота появления события будет сколь угодно мало отличаться от вероятности при большом числе n, т.е. p = Всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями, есть закон распределения случайной величины. Закон распределения случайной величины может быть задан в разных формах: а) ряд распределения (для дискретных величин); б) функция распределения; в) кривая распределения (для непрерывных величин).
Кривая нормального распределения была дана немецким математиком К.Ф.Гауссом в 1821 г.:
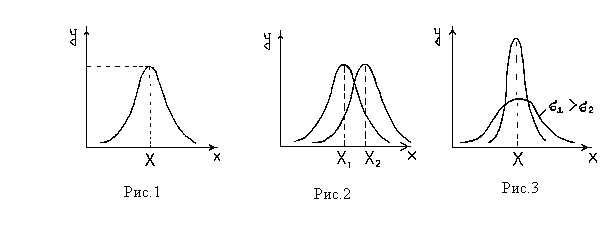
где у(xi) - ордината кривой нормального распределения (плотность вероятности случайной величины); x - значение случайной величины; m - “истинное” значение величины (среднее арифметическое или математическое ожидание случайной величины); s - среднее квадратичное отклонение; e - основание натуральных логарифмов (e=2.7183). а) Основные свойства кривой Гаусса. - Кривая имеет колоколообразную форму. На некотором расстоянии от середины симметрично по обе стороны ее находятся точки перегиба (Рис.1). Характеристиками кривой служат высота кривой и расстояния от оси ординат до точек перегиба. - Вершина кривой соответствует наибольшему числу повторений, т.е. наибольшей вероятности, соответствующей погрешности =0. - При увеличении абсолютной погрешности вероятность ее появления уменьшается. Кривая асимптотически приближается к оси абсцисс; следовательно, появление больших погрешностей маловероятно. - Кривая нормального распределения симметрична относительно вертикальной оси, проходящей через максимум кривой, т.е. одинаковые погрешности, но с разными знаками имеют одинаковую вероятность. Из формулы (1) видно, что центр рассеивания x = m является центром симметрии и, если изменять центр рассеивания m, кривая распределения будет смещаться вдоль оси абсцисс, не изменяя своей формы (Рис.2). - параметр s определяет саму форму кривой распределения. Максимум функции нормального распределения при x=m равен:
т.е. обратно пропорционален величине s. Площадь, ограниченная кривой распределения всегда равна 1:
поскольку (3) выражает вероятность того, что случайная величина примет какое-нибудь значение из интервала (-¥, +¥) - достоверное событие. Поэтому при увеличении кривая распределения становится пологой, т.е. сжимается к оси Ох и растягивается вдоль неё (Рис.3).
б) Правила обработки результатов измерений.
Указанные правила можно применять при нормальном распределении результатов измерений или мало отличающемся от него. 1) Определяют среднее арифметическое значение измеряемой величины:
2) Находят абсолютные погрешности отдельных измерений:
3) Вычисляют среднюю абсолютную погрешность отдельных измерений:
4) Вычисляют среднюю квадратическую погрешность отдельных измерений: s=1.253 x, или 5) Отбрасывают промахи, если Dxi> 3s. 6) Определяют среднюю квадратическую погрешность среднего значения: s = 1.253å Dxi/n или s = s/ 7) По числу наблюдений n< 30 и выбранной доверительной вероятности a по таблицам Стьюдента (см. приложение) определяют коэффициент Стьюдента ta, n. 8) Записывают величину доверительного интервала для среднего значения измеряемой величины: Dx = ta, n∙ s. 9) Записывают результат измерений: x = 10) Определяют относительную погрешность: E=
|

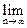 p*, p - статистическая вероятность события.
p*, p - статистическая вероятность события. (1)
(1)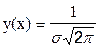 (2)
(2) (3)
(3)
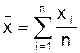 .
.
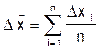
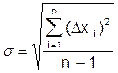 .
. = 1.253
= 1.253  ,
,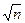 =
= 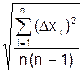 .
.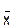 ±Dx
±Dx



