Ход работы. Упражнение 1.Измерение длительности полных сердечных сокращений
Упражнение 1 .Измерение длительности полных сердечных сокращений (SR-R). 1)Исследуя 30 интервалов зубцов R-R, на ленте с электрокардиограммой, без пропусков и повторов запишите в таблицу № 1 значения Si(мм). Затем для каждого Si рассчитайте время полного сердечного сокращения t (Если значений t Таблица №1.
tmin= tmax=
и вычислите величину интервала по формуле:
Δ t=
Упражнение 2. Проверка эмпирического распределения на нормальный закон (построение гистограммы).
1) Прочитайте в пункте III раздел 1.Построение гистограммы. 2) Заполните таблицу №2 (статистический ряд). Для этого:
а) разбейте весь диапазон значений времени t б) рассчитайте и запишите в таблицу №2 среднее интервальное времени для каждого интервала
в) подсчитайте число m значений времени, попавших в каждый интервал (при этом ∑ mi=30!); г) по формуле Р* д) найдите значения Р*
Таблица № 2.
Расчёты:
е) как на рис. 4 постройте гистограмму т.е зависимость Р*
ж) по виду полученной гистограммы проведите анализ вашего распределения;
з) вычислите среднеарифметическое значение времени:
И среднее квадратическое отклонение
расчёты:
D =
σ =
и) дополните проверку на нормальность распределения по коэффициентам А, Е, σ к) если полученная гистограмма отличается от гистограммы на Рис.3 продолжите проверку на нормальность распределения по критерию Колмогорова (пункт III, раздел 3 данного пособия). Полученные значения занесите в Табл.3 " Критерий Колмогорова";
Упражнение № 3. Построение кривой нормального распределения Заполните Таблицу №3.
Таблица №3.
где
z σ - среднее квадратическое отклонение; f (z f( - Постройте график функции у=f( - Отметьте максимум кривой распределения на графике. - Проведите статистическую обработку результатов измерений в соответствии с формулами в главе II раздел б). - Сделайте вывод о распределении значений времени полного сердечного сокращения. - Результат измерений запишите в виде доверительного интервала сдоверительной вероятностью 0.95: где Dt = ta, n∙ S, ta, n = 2, 042 – коэффициент Стьюдента, а S = s/ Расчёты:
S = Dt =
t=(±), с
Определите относительную погрешность измерений: E= Е =
По результатам выполненной работы записать вывод: ____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Подпись преподавателя: ___________________________________________________
«»______________201_г.
|

 по формуле 16.
по формуле 16. (мм)
(мм)
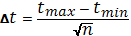 , где n=30 – количество измерений.
, где n=30 – количество измерений. и ti, max , и величиной интервала Δ t
и ti, max , и величиной интервала Δ t
 , с
, с
 , с
, с
 , с
, с
 , с
, с



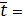
 , где
, где 
 , σ
, σ  - формулы (8, 9, 10, 11), соответственно;
- формулы (8, 9, 10, 11), соответственно; , с
, с
 ), с
), с
 - среднее арифметическое значение времени (смотри выше);
- среднее арифметическое значение времени (смотри выше);

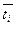 ) в одной системе координат с гистограммой.
) в одной системе координат с гистограммой.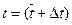 , с
, с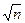 - средняя квадратическая погрешность среднего значения
- средняя квадратическая погрешность среднего значения



