Матрица парных корреляций
Как следует из табл 4.12, все исследуемые показатели имеют между собой тесную корреляционную связь. Поэтому в соответствии с канонами классического регрессионного анализа построение многофакторного регрессионного уравнения некорректно (из-за наличия колинеарности). Кроме того, и размеры статистических рядов накладывают свои ограничения. Тем не менее, даже чисто визуальный анализ динамических рядов, представленных на рис. 4.11, говорит о том, что искомая взаимосвязь существует. Проблема состоит в том, как обойти ограничения, накладываемые требованиями формальных статистических методов обработки данных. Предлагается построить некую, на первый взгляд, искусственную конструкцию, представляющую собой разность индексов производительности труда и объёма производства (ВВП). Это позволит, во-первых, снизить размерность (количество независимых факторов), во-вторых, хотя бы частично устранить имеющуюся мультиколлинеарность. Как оказалось, полученный таким образом динамический ряд имеет явно выраженную тенденцию и хорошо описывается трендовой моделью в виде квадратичной параболы, где х - временная переменная (см. рис 4.9). Нетрудно заметить, что данная трендовая зависимость имеет максимум «в районе» 1998 г., за которым движение по ней идет уже по нисходящей ветви. Это можно интерпретировать, как перелом в сложившихся тенденциях. И действительно, такой перелом имеет место. Если до 1999 г. наблюдалась устойчивая тенденция снижения численности занятых, то по данным Госкомстата России в 1999 г. при росте ВВП на 3, 2% численность занятых выросла на 900 тыс. человек. При этом выросла и производительность труда, что говорит о том, что увеличился не только совокупный, но и за счет сокращения скрытой безработицы удовлетворенный эффективный спрос на рабочую силу. Тем не менее, трендовая модель, хотя и правильно описывает качественные сдвиги в динамике спроса на рабочую силу, имеет существенный недостаток в том, что не учитывает инвестиционный фактор. Дальнейший анализ показал очень тесную корреляционную связь между динамикой индекса инвестиций и разностью индексов производительности труда и объема ВВП (коэффициент корреляции более 0, 98). Поэтому была предпринята попытка построения регрессионного уравнения зависимости разности индексов производительности труда и ВВП от индекса инвестиций. Было получено следующее уравнение:
где d - разность индексов производительности труда и объема ВВП; Ji - индекс инвестиций. Коэффициенты регрессии значимы по критерию Стьюдента, а сама модель - по критерию Фишера. Верификация данной модели, построенной на базе динамических рядов, приведенных в табл 4.11, на отчетных данных 1999 г. показала, что модель не только правильно учла перелом в тенденциях анализируемых показателей, но и ошибка при оценке численности занятых в экономике не превысила 4%, что говорит о ее высокой адекватности реально происходящим процессам. Алгоритм прогнозных расчетов по предлагаемой модели достаточно прост и состоит в следующем. Цепные индексы показателей занятости, ВВП и инвестиций за ряд лет преобразуются в базисные индексы (см. табл 4.8). Рассчитываются индексы производительности труда по формуле:
где JP – индекс производительности труда; JV – индекс объема производства; JЧ - индекс численности занятых.
Рассчитывается разность индексов производительности труда и объемов производства:
Строится линейное регрессионное уравнение вида:
На основе статистических рядов базовых индексов оцениваются значения коэффициентов регрессии. Предлагаемая модель прогнозирования имеет два независимых параметра - объем производства (ВВП) и объем инвестиций, задаваемых величиной индексов соответствующих показателей. Значения этих параметров могут задаваться исходя из различных условий, например на основе тех или иных сценариев макроэкономического развития, тогда получаем вариантный прогноз динамики спроса на рабочую силу, или исходя из данных официально утвержденного целевого макроэкономического прогноза. Зная прогнозную динамику инвестиций и объемов производства (ВВП), на основании уравнения (4) рассчитывается величина разности индексов производительности труда и объемов производства для каждого года прогнозного периода, а также собственно величина индекса производительности труда в прогнозном периоде по формуле:
Прогнозное значение индекса численности занятых несложно получить из соотношения:
Для расчета абсолютной величины спроса на рабочую силу достаточно скорректировать абсолютные значения численности занятых, полученные на основе индекса численности, рассчитанного по формуле (6), на число вакантных рабочих мест для каждого года прогнозного периода. Данная методика может быть использована для прогнозирования занятости и спроса на рабочую силу как на федеральном, так и на региональном уровнях, как для экономики страны в целом, так и для отдельных ее отраслей, а также отраслей промышленности. В качестве иллюстрации (табл 4.13) приводятся прогнозные оценки занятости в экономике России на период до 2003 г. Таблица 4.13
|

 , (1)
, (1) , (2)
, (2) . (3)
. (3)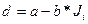 . (4)
. (4) . (5)
. (5) . (6)
. (6)


