Формализованное описание экономических систем как систем массового обслуживания и методы их исследования
Для описания любой системы массового обслуживания необходимо установить: 1) общее число источников требований (N) и взаимосвязи между ними, 2) количество каналов обслуживания (m); 3) входящий поток требований (A); 4) поток обслуживания (B); 5) количество мест ожидания (K), 6) дисциплину и доступность обслуживания; 7) для многофазных систем – матрицу передач между фазами. Таким образом, любую систему массового обслуживания можно формально описать следующим образом: A/B/m/K/N, где A-входной поток требований, B-поток обслуживания, N-общее число источников требований, m-количество каналов обслуживания, K-количество мест ожидания. Входящий поток требований – это последовательность требований, поступающих в систему для обслуживания (совокупность периодичностей обслуживания). В очень редких случаях требования поступают через одинаковые промежутки времени и такие потоки называют регулярными. Однако, в большинстве случаев поток требований носит случайный характер и описывается математическим ожиданием ( Вместо значения средней периодичности поступления заявок (
где l - интенсивность потока требований,
Поток обслуживания – это совокупность длительностей обслуживания; для его характеристики необходимо также указать математическое ожидание ( Вместо средней длительности обслуживания – обратную величину, которая называется средней интенсивностью потока обслуживания ( Для практических расчетов наиболее важными являются два вида потоков требований: 1. Простейший, который создается большим числом источников требований и характеризуется следующими свойствами: - ординарностью, - стационарностью, - отсутствием последействия. Ординарность – невозможность одновременного поступления двух или более требований в бесконечно малый промежуток времени. Стационарность - предполагает, что средняя интенсивность потока не изменяется с течением времени. Отсутствие последействия - вероятность поступления требований в определенный промежуток не зависит от предшествующего течения процесса. 2. С простым последействием – поток формируется конечным числом источников требований и интервалы времени между поступлениями соседних требований распределяются по экспоненциальному закону (пример, ремонт и обслуживание оборудования) Для многофазных систем необходимо определить маршруты требований между фазами, что задается в виде матрицы, содержащей вероятности перехода требований между фазами.
Матрица передач для многофазной системы
где Pij – характеризует вероятность перехода требования от i-фазы к j-фазе. n – количество фаз обслуживания
Описав входные параметры системы массового обслуживания, необходимо определить показатели, характеризующие результаты ее работы (рис. 4.6, 4.7).
Рис. 4.6. Схема моделирования в теории массового обслуживания
Для расчета указанных результирующих характеристик СМО разработаны аналитические зависимости: для каждого типа системы свои зависимости. Вместе с тем теория массового обслуживания – относительно молодая наука, аналитические зависимости в которой разработаны лишь для очень ограниченного числа систем массового обслуживания. Это, в основном, системы с экспоненциальным распределением длительности обслуживания и интервалов между моментами требований. В остальных случаях для расчета результирующих характеристик рекомендуется использовать имитационное моделирование на ПЭВМ.
Рис. 4.7. Схема применения теории массового обслуживания для оптимизации хозяйственных систем
Практический пример. Разработка норм численности с использованием ТМО (15)
Имеется инструментальный склад, обслуживающий несколько цехов фирмы. Аналитически известны интенсивность потока требований на инструмент λ и интенсивность потока обслуживаний μ за смену. Известны также потери в единицу времени: от простоя в очереди - n усл. ед., на содержание кладовщика - т усл. ед. Менеджеров, организующих производственный процесс, интересует среднее время ожидания обслуживания и среднее время обслуживания при разном количестве кладовщиков s инструментального склада. Также важно найти оптимальное количество кладовщиков с учетом затрат в единицу времени на простой в очереди и на содержание кладовщика.
Методика решения задачи: При работе одного кладовщика данную задачу можно представить в виде одноканальной системы обслуживания с неограниченной очередью. ρ = При ρ > 1 очередь растет неограниченно. При ρ < 1 имеем следующие показатели. Вероятность отсутствия очереди: p 0 = 1 - ρ Вероятность очереди из (k - 1) заявок: pk = ρ k (1 - ρ) или pk = ρ kp 0 Среднее время ожидания в системе Tc = 1/μ (1/(1 - ρ)). Tc = Тож + Тобс Среднее время ожидания обслуживания: Тож = 1/μ (1/(1 - ρ)). Среднее время обслуживания: Тобс = 1/μ При работе s кладовщиков задачу можно описать как многоканальную систему с неограниченной очередью. Если ρ / s < 1, то существуют финальные вероятности. Если ρ / s ≥ 1, то очередь растет до бесконечности. При этом ρ может быть больше 1. Предположим, что условие (ρ / s) < 1 выполнено. Тогда вероятность отсутствия очереди равна: p0= Среднее число заявок в очереди: Lоч= Среднее число заявок в системе (с учетом уже обслуживающихся заявок): Lc=Lоч+p. Среднее время пребывания заявки в очереди: Точ= Среднее время пребывания заявки в системе: Тс= Предположим, что затраты в единицу времени на простой составляют 7 усл. ед., а на содержание одного кладовщика 5 усл. ед. Тогда получим следующие результаты при разном количестве кладовщиков (полагаем, что λ = 1, 6, μ = 0, 9, р = 1, 77). При s=2: Тс = 5, 11, общие затраты 7*5, 11 + 5*2 = 45, 77 усл. ед. При s=3: Тс= 1, 42, общие затраты 7 * 1, 42 + 5 * 3 = 24, 94 усл. ед. При s=4: Тc = 1, 17, общие затраты 7 * 1, 17 + 5 * 4 = 28, 19 усл. ед. Видно, что с экономической точки зрения выгодно держать на складе трех кладовщиков. Варианты заданий 1 (рассчитать показатели работы СМО для одного кладовщика)
Варианты заданий 2 (рассчитать показатели работы СМО для 2, 3,..., 5 кладовщиков, принять решение об их оптимальном количестве с учетом затрат на простой n и на содержание одного кладовщика m)
|
), характеристиками рассеяния (V), видом закона распределения интервалов между моментами поступления требований на обслуживание.
,
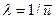) и степень рассеивания (V) и закон распределения интервалов длительности обслуживания.
).
.
.
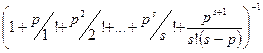
