Модели структуры содержательных характеристик явлений
1. Модели снижения размерности многомерных географических данных 1.1. Факторный анализ 1.2. Метод главных компонент 2. Моделирование типологических синтетических характеристик 3. Моделирование оценочных синтетических характеристик Методы факторного и компонентного анализа опираются на предположение, что наблюдаемые признаки являются косвенными проявлениями небольшого числа скрытых факторов. Методы направлены на выявление и анализ скрытых зависимостей между этими признаками. В факторном анализе исследуют внутреннюю структуру матрицы корреляции, основываясь на предположении, что множество наблюдаемых коррелированных признаков можно описать меньшим числом определяющих факторов и множеством независимых остатков в виде их линейной комбинации Компонентный анализ основан на использовании ковариационной матрицы для проведения линейного ортогонального преобразования пространства признаков с тем, чтобы в новой системе координат признаки были взаимно некоррелированы. Матрицу ортопреобразования можно представить в виде: R= Факторный анализ предпочтителен, когда хотят выделить районы, однородные по всему комплексу показателей, на основе построения их линейной комбинации – факторов (целесообразно применять для определения структуры данных) Компонентный анализ – при дифференциации территории на основе ведущих признаков с учетом их взаимосвязей (например, по факторам рельефа – высота, экспозиция, крутизна) – основной метод сокращения данных и их размерности.
Условие создания моделей типологических характеристик – однородность территориальных единиц, объединяемых в одну группу, и максимальная гетерогенность между однородными таксонами (пример- классификация с/х предприятий по специализации). Основной метод – метод «вроцлавской таксономии». Он предполагает нормировку матрицы исходных показателей по дисперсиям: Второй метод – метод Тикунова. Основан на предыдущем методе, но без построения графов. Из итоговой матрицы d выбирается наибольшее евклидово расстояние. Две точки, которые оно связывает становятся ядрами, вокруг которых будут образовываться будущие группы. В зависимости от евклидовых расстояний все оставшиеся n-2 точки будут распределены между двумя ядрами. При формировании трех групп алгоритм работает следующим образом: два ядра остаются, а третье находится так. Каждая из n-2 точек опробуется в качестве третьего ядра, а n-3 оставшихся распределяются между тремя ядрами по минимальности евклидовых расстояний. Для каждого варианта группировки подсчитывается сумма внутригрупповых различий, и тот вариант, который дает наименьшую сумму, принимается за третье ядро. Аналогично – для четырех и более групп. Практическая реализация – природно-хозяйственная типология Кольского полуострова. Условие создания моделей оценочных характеристик – гомогенность территориальных единиц, образующих иерархически упорядоченные таксоны. Три алгоритма Тикунова. Первый алгоритм. А) нормировка показателей территориальных единиц Б) построение матрицы D из нормированных единиц В) ранжирование территориальных единиц по шкале их интегрального оценочного положения Г) расчет векторов различий d относительно территориальной единицы с лучшими или экстремальными оценочными условиями в матрице Д) ранжирование векторов d по возрастанию Е) распределение исходных территориальных единиц по таксонам в зависимости от показателей приращений последующих ранжированных значений d над предыдущими (нахождение минимального приращения – связывание территориальных единиц в таксон – поиск нового минимального приращения) Для случая с большими относительными различиями в характеристиках высоко оцениваемых территориальных единиц и нивелировкой значений для низко оцениваемых единиц (высокогорья с большим расчленением рельефа и нерасчлененная низменность) применяются следующие методы: - второй алгоритм А) повторная раздельная классификация высоко и низко оцениваемых территориальных единиц Б) модификация первого алгоритма с приращениями (замена показателей объединенных в один таксон территориальных единиц на осредненный показатель с вычислением новых приращений до тех пор пока все территориальные единицы не сольются в одну группу) В) нормировка приращений с учетом веса точек ряда (при объединении двух единиц – вес равен двойке, при объединении трех единиц – тройке и т.д.) Практическая реализация – определение уровня соц-экономического развития 80 стран Африки, Азии и Латинской Америки относительно эталонного показателя США и вычисление степени сельскохозяйственного воздействия на окружающую среду Калмыкии. Билет №20
|

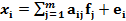 , где
, где  – совокупность исходных признаков; f –значения общего j-го фактора; a –коэффициенты при f; m – количество факторов; e – независимые остатки. Матрица коэффициентов «a» называется матрицей факторных нагрузок и задает влияние общих факторов.
– совокупность исходных признаков; f –значения общего j-го фактора; a –коэффициенты при f; m – количество факторов; e – независимые остатки. Матрица коэффициентов «a» называется матрицей факторных нагрузок и задает влияние общих факторов. V, гдеV – матрица собственных векторов преобразования (определяет поворот осей), E – диагональная матрица собственных значений γ;; T – операция транспонирования, R –корреляционная матрица. При решении уравнения выбирают максимальное значение γ 1 и соответствующий ему вектор V1. Это главная компонента, обладающая наибольшей дисперсией (отклонением от среднего). Аналогично определяют остальные главные компоненты, после чего отбрасывают компоненты с минимальными дисперсиями.
V, гдеV – матрица собственных векторов преобразования (определяет поворот осей), E – диагональная матрица собственных значений γ;; T – операция транспонирования, R –корреляционная матрица. При решении уравнения выбирают максимальное значение γ 1 и соответствующий ему вектор V1. Это главная компонента, обладающая наибольшей дисперсией (отклонением от среднего). Аналогично определяют остальные главные компоненты, после чего отбрасывают компоненты с минимальными дисперсиями. = (
= ( -
- 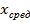 )/σ. Нормированные показатели (
)/σ. Нормированные показатели (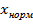 ) образуют новую матрицу, на основе которой рассчитываются евклидовы расстояния. Все таксоны представлены в виде точек в m-мерном пространстве (m- число столбцов в матрице). Координаты точек -
) образуют новую матрицу, на основе которой рассчитываются евклидовы расстояния. Все таксоны представлены в виде точек в m-мерном пространстве (m- число столбцов в матрице). Координаты точек -  ), соединяющие каждую пару точек, отражают различия свойств таксонов, на чем и основывается дифференциация территории
), соединяющие каждую пару точек, отражают различия свойств таксонов, на чем и основывается дифференциация территории  -
-  )².Все рассчитанные расстояния
)².Все рассчитанные расстояния  = (
= ( )/(
)/( -
-  ).Она позволяет выразить отклонения всей системы показателей от наилучших оценочных значений и тем самым правильнее соизмерить их между собой.
).Она позволяет выразить отклонения всей системы показателей от наилучших оценочных значений и тем самым правильнее соизмерить их между собой.


