О РАЗЛИЧНЫХ КЛАССАХ ПОНЯТИЙ
ОПРЕДЕЛЕНИЕ И ЗАДАЧИ ЛОГИКИ Определение логики. Для того чтобы определить, что такое логика, мы должны предварительно выяснить, в чём заключается цель человеческого познания. Цель познания заключается в достижении истины при помощи мышления, цель познания есть истина. Логика же есть наука, которая показывает, как должно совершаться мышление, чтобы была достигнута истина; каким правилам мышление должно подчиняться для того, чтобы была достигнута истина. При помощи мышления истина иногда достигается, а иногда не достигается. То мышление, при помощи которого достигается истина, должно быть названо правильным мышлением. Таким образом, логика может быть определена какнаука о законах правильного мышления, или наука о законах, которым подчиняется правильное мышление. Из этого определения видно, что логика исследует законы мышления. Но так как исследование законов мышления как известного класса психических процессов является также предметом психологии, то предмет логики выяснится лучше в том случае, если мы рассмотрим отличие логики от психологии в исследовании законов мышления. Психология и логика. На мышление мы можем смотреть с двух точек зрения. Мы можем на него смотреть прежде всего как на известный процесс, законы которого мы исследуем. Это будет точка зрения психологическая. Психология изучает, как совершается процесс мышления. С другой стороны, мы можем смотреть на мышление, как на средство достижения истины. Логика исследует, каким законам должно подчиняться мышление, чтобы оно могло привести к истине. Итак, разница между психологией и логикой в отношении к процессу мышления может быть выражена следующим образом. Психология рассматривает безразлично всевозможные роды мыслительной деятельности: рассуждение гения, бред больного, мыслительный процесс ребёнка, животного — для психологии представляют одинаковый интерес, потому что она рассматривает только, как осуществляется процесс мышления; логика же рассматривает условия, при которых Мысль может быть правильной. В этом отношении логика сближается с грамматикой. Подобно тому, как грамматика указывает правила, которым должна подчиняться речь, чтобы быть правильной, так логика указывает нам законы, которым должно подчиняться наше мышление для того, чтобы быть правильным. Для того чтобы понять утверждение, что существуют известные правила, которым должно подчиняться мышление, рассмотрим, в чём заключается задача логики. Задача логики. Есть положения или факты, истинность которых усматривается непосредственно, и есть положения или факты, истинность которых усматривается посредственно, именно через посредство других положений или фактов. Если я скажу: «я голоден», «я слышу звук», «я ощущаю тяжесть», «я вижу, что этот предмет большой», «я вижу, что этот предмет движется» и т. п., то я выражу факты, которые должны считаться непосредственно познаваемыми. Такого рода факты мы можем назвать также непосредственно очевидными, потому что они не нуждаются ни в каком доказательстве: их истинность очевидна без доказательств. В самом деле, разве я нуждаюсь в доказательстве, что передо мной находится предмет, имеющий зелёный цвет? Неужели, если бы кто-нибудь стал доказывать, что этот предмет не зелёный, а чёрный, я поверил бы ему? Этот факт для меня непосредственно очевиден. К числу непосредственно очевидных положений относятся, прежде всего, те положения, которые являются результатом чувственного восприятия. Все те факты, которые совершаются в нашем отсутствии (например, прошедшие явления, а также и будущие), могут быть познаваемы только посредственно. Я вижу, что дождь идёт, — это факт непосредственного познания; что ночью шёл дождь, есть факт посредственного познания, потому что я об этом узнаю через посредство другого факта, именно того факта, что почва мокрая. Факты посредственного познания или просто посредственное познание является результатом умозаключения, вывода. По развалинам я умозаключаю, что здесь был город. Если бы я был на этом месте тысячу лет назад, то я непосредственно воспринял бы этот город. По следам я заключаю, что здесь проехал всадник. Если бы я был здесь час назад, то я непосредственно воспринял бы самого всадника. Посредственное знание доказывается, делается убедительным, очевидным при помощи знаний непосредственных. Этот последний процесс называется доказательством. Таким образом, есть положения, которые не нуждаются в доказательствах, и есть положения, которые нуждаются в доказательствах и очевидность которых усматривается посредственно, косвенно. Если есть положения, которые нуждаются в доказательствах, то в чём же заключается доказательство? Доказательство заключается в том, что мы положения неочевидные стараемся свести к положениям или фактам непосредственно очевидным или вообще очевидным. Такого рода сведение положений неочевидных к положениям очевидным лучше всего можно видеть на доказательствах математических; Если возьмём, например, теорему Пифагора, то она на первый взгляд совсем не очевидна. Но если мы станем её доказывать, то, переходя от одного положения к другому, мы придём в конце концов к аксиомам и определениям, которые имеют непосредственно очевидный характер. Тогда и самая теорема сделается для нас очевидной. Таким образом, познание посредственное нуждается в доказательствах; познание непосредственное в доказательствах не нуждается и служит основой для доказательства познаний посредственных. Заметив такое отношение между положениями посредственно очевидными и положениями непосредственно очевидными, мы можем понять задачи логики. Когда мы доказываем что-либо, т. е. когда мы сводим неочевидные положения к непосредственно очевидным, то в этом процессе сведения мы можем сделать ошибку: наше умозаключение может быть ошибочным. Но существуют определённые правила, которые показывают, как отличать умозаключения правильные от умозаключений ошибочных. Эти правила указывает логика. Задача логики поэтому заключается в том, чтобы показать, каким правилам должно следовать умозаключение, чтобы быть верным. Если мы эти правила знаем, то мы можем определить, соблюдены ли они в том или другом процессе умозаключения. Из такого определения задач логики можно понять значение логики. Значение и польза логики. Для выяснения значения логики обыкновенно принято исходить из определения её. Мы видели, что логика определяется как наука о законах правильного мышления. Из этого определения логики, невидимому, следует, что стоит изучить законы правильного мышления и применять их в процессе мышления, чтобы можно было мыслить вполне правильно. Многим даже кажется, что логика может указывать средства для открытия истины в различных областях знания. Но в действительности это неверно. Логика не поставляет своею целью открытие истин, а ставит своею целью доказательство уже открытых истин. Логика указывает правила, при помощи которых могут быть открыты ошибки. Вследствие этого, благодаря логике можно избежать ошибок. Поэтому становится понятным утверждение английского философа Д.С. Милля, что польза логики главным образом отрицательная. Её задача заключается в том, чтобы предостеречь от возможных ошибок. Вследствие этого практическая важность логики чрезвычайно велика. «Когда я принимаю в соображение, — говорит Д. С. Милль, — как проста теория умозаключения, какого небольшого времени достаточно для приобретения полного знания её принципов и правил и даже значительной опытности в их применении, я не нахожу никакого извинения для тех, кто, желая заниматься с успехом каким-нибудь умственным трудом, упускает это изучение. Логика есть великий преследователь тёмного и запутанного мышления; она рассеивает туман, скрывающий от нас наше невежество и заставляющий нас думать, что мы понимаем предмет, в то время когда мы его не понимаем. Я убеждён, что в современном воспитании ничто не приносит большей пользы для выработки точных мыслителей, остающихся верными смыслу слов и предложений и находящихся постоянно настороже против терминов неопределённых и двусмысленных, как логика». Многие часто ссылаются на так называемый здравый смысл и говорят: «Да ведь ошибки можно находить без помощи логики, посредством лишь одного здравого смысла». Это, конечно, справедливо, но часто бывает недостаточно найти ошибку, нужно ещё объяснить её, уметь точно охарактеризовать и даже обозначить её. Иной знает, что в том или другом умозаключении есть ошибка, но он не в состоянии сказать, почему это умозаключение нужно считать ошибочным. Это часто возможно сделать только благодаря знанию правил логики. Логика имеет также значение для определения взаимного отношения между науками. Различие между науками, например математическими, физическими и историческими, может стать ясным только в том случае, если мы рассмотрим различие методов познания с логической точки зрения. История логики и главное направление её. Творцом логики как науки следует считать Аристотеля (384—322). Логика Аристотеля имела господствующее значение не только в древности, но также и в средние века, в эпоху так называемой схоластической философии. Заслуживает упоминания сочинение последователей философа Декарта (1596—1650), которое называлось: La logique ou lart de penser (1662). Эта логика, которая называется логикой Port, которая, принадлежит к так называемому формальному направлению. В Англии Бэкон (1561—1626) считается основателем особого направления в логике, которое называется индуктивным, наилучшими выразителями которого в современной логике являются Д.С. Милль (1806—1873) и Л. Бэн (1818—1903). Для того, чтобы понять, в чем заключается различие между формальным и индуктивным направлением в логике, заметим, что называется материальной и формальной истинностью. Мы считаем какое-либо положение истинным материально, когда оно соответствует действительности или вещам. Мы считаем то или другое заключение истинным формально в том случае, когда оно выводится с достоверностью из тех или иных положений, т.е., когда верен способ соединения мыслей, самое же заключение может совсем не соответствовать действительности. Для объяснения различия между формальной и материальной истинностью возьмём примеры, нам даются два положения: Все вулканы суть горы Все гейзеры суть вулканы Из этих двух положений с необходимостью следует, что «все гейзеры суть горы». Это заключение формально истинно, потому что оно с необходимостью следует из двух данных положений, но материально оно ложно, потому что оно не соответствует действительности; гейзеры не суть горы. Таким Образом, умозаключение истинное формально может быть ложным материально. Но возьмём следующий пример: Все богачи тщеславны Некоторые люди не суть богачи След., некоторые люди не суть тщеславны. Это заключение истинно материально, потому что действительно «некоторые люди не суть тщеславны», но оно формально ложно, потому что не вытекает из данных положений. В самом деле, если бы было сказано, что только богачи тщеславны, тогда о всяком не-богаче мы сказали бы, что он не тщеславен. Но у нас в первом положении утверждается: «все богачи тщеславны»; этим не исключается, что и другие люди могут быть тщеславными. В таком случае можно быть небогатым и в то же время быть тщеславным; из того, что кто-нибудь не есть богач, не следует, что он не может быть тщеславным. Из этого ясно, что указанное заключение не вытекает из данных положений необходимо. Те правила, которые указывают, когда получаются заключения истинные формально, мы можем назвать формальными критериями истинности; те правила, которые определяют материальную истинность, мы можем назвать материальными критериями истинности. Формальная логика по преимуществу изучает те отделы логики, в которых может быть применяем формальный критерий истинности. Индуктивная логика, в противоположность формальной логике, по преимуществу разрабатывает те отделы, в которых применяется материальный критерий. Вопросы для повторения Как определяется логика? Какое различие существует между психологией и логикой? Какие положения можно считать непосредственно очевидными? Какие положения нужно считать посредственно очевидными? В чём заключается задача доказательства? В чём заключается задача логики? Почему «здравый смысл» не может заменить логики? Какие существуют основные направления в логике?
Глава II О РАЗЛИЧНЫХ КЛАССАХ ПОНЯТИЙ Понятия и термины. Мы предполагаем начать с рассмотрения различных классов понятий. В сочинениях по логике у английских философов изложение логики обыкновенно начинается с рассмотрения терминов, имён или названий. Они исходят из того, что в логике мы должны трактовать не просто о понятиях, которые представляют известные умственные построения, но мы должны о них трактовать постольку, поскольку они получают выражение в языке, в речи; а так как понятия мы выражаем при помощи слов, названий и т. п., то, по их мнению, гораздо целесообразнее в логике говорить не о понятиях, а о названиях, именах или терминах. Таким образом, мы можем рассматривать или понятия в том виде, как они нами мыслятся, илиих выражение при помощи слов. Но на самом деле между этими двумя рассмотрениями нет существенной разницы. Каждое понятие у нас в мышлении фиксируется, приобретает устойчивость, определённость благодаря тому или другому слову, названию, термину. Когда мы в логике, оперируем с понятием, то мы всегда имеем в виду понятие, которое связывается с известным словом. Слово является заместителем понятий. Мы можем оперировать только с теми понятиями, которые получили своё выражение в речи. Таким образом, ясно, что всё равно, будем ли мы говорить о названиях и терминах, как это делается в английской логике, или же будем говорить о понятиях просто. Понятия индивидуальные и общие. Понятия разделяются прежде всего на индивидуальные, или единичные, и общие. Индивидуальными понятиями мы будем называть те понятия, которые относятся к предметам единичным, индивидуальным (в данном случае индивидуальные понятия совпадают с представлениями о единичных вещах), например: «британский посланник во Франции», «высочайшая гора в Америке», «автор «Мёртвых душ», «эта книга». К числу единичных понятий относятся также и собственные имена, например: «Казбек», «Ньютон», «Рим». Понятия, которые относятся к группе или классу предметов или явлений, имеющих известное сходство между собой, называются общими понятиями или классовыми понятиями. Например, понятия «растение», «животное», «газ», «двигатель», «поступок», «движение», «красота», «гнев», «чувство» и т. п. суть понятия классовые или общие. Общие, собирательные и разделительные термины. Единичные и общие понятия иногда могут употребляться в особенном смысле, и именно в так называемом собирательном. Если я произнесу предложение: «лес служит для сохранения влаги», то в этом предложении «лес» есть один из множества однородных предметов; в этом предложении понятие «лес» употреблено в общем смысле. Но «лес» может представляться как одно целое, состоящее из однородных единиц. В таком случае понятие «лес», или термин «лес», делается коллектив-н ы м, или собирательным. Собирательный термин обозначает одно целое, группу, состоящую из однородных единиц. Например, термины «полк», «толпа», «библиотека», «лес», «парламент», «созвездие», «соцветие», «класс» представляют собой собирательные термины, если мы имеем в виду, что они служат для обозначения целого, составленного из однородных единиц. Но эти же самые термины делаются общими, когда мы их мыслим отдельными представителями известного класса. Например, «полк», «толпа» есть общий термин, когда речь идёт о «полках», о «толпах»; в этом случае вещи, обозначенные этими терминами, рассматриваются как известные единицы, входящие в состав известного класса сходных вещей. Если я употребляю термины «Пушкинская библиотека», «английский парламент», то я употребляю термины собирательные, потому что они выражают известное целое, составленное из однородных единиц. Если же я скажу «европейские библиотеки, парламенты, университеты» и т. д., то это суть общие термины, потому что я говорю о библиотеках, парламентах, университетах как известном классе сходных предметов. Как это видно из приведённых примеров, собирательные понятия представляют собой особую форму индивидуальных понятий. Так как весьма часто общие понятия можно смешать с собирательными, то следует обратить внимание на следующее различие между ними. То, что мы утверждаем относительно понятия собирательного, относится к известному целому, составленному из единичных предметов, но это утверждение может быть неприложимо к предметам, входящим в это целое и взятым в отдельности. Наоборот, то, что мы утверждаем относительно общего понятия, может быть приложено к каждому предмету, к которому относится это понятие. Собирательное понятие мыслится как одно целое, состоящее из однородных единиц; общее понятие мыслится как класс, который состоит из сходных предметов. Если мы говорим «парламент издал закон о всеобщей воинской повинности», то мы этим хотим сказать, что известное целое, составленное из известных единиц, издало известный закон, но этого нельзя сказать относительно каждого члена парламента, потому что отдельные члены парламента могут высказаться за сохранение прежнего порядка отбывания воинской повинности. В этом случае понятие «парламент» употреблено в собирательном смысле. Но я могу употребить выражение «парламенту принадлежит законодательная функция»; в этом случае термин «парламент» употреблён в общем смысле, потому что указанное выражение справедливо относительно всех парламентов. Иногда мы можем употреблять те или иные понятия таким образом, что наши утверждения будут справедливы относительно каждой отдельной единицы, входящей в ту или другую группу предметов. Такое употребление терминов, или понятий, мы будем называть употреблением в разделительном смысле. Когда мы употребляем какое-нибудь понятие в собирательном смысле, то мы наше утверждение относим к группе, рассматриваемой в целом; если же мы употребляем его в смысле разделительном, то мы утверждаем что-либо о каждом члене группы раздельно. Если мы, например, говорим: «весь флот погиб во время бури», то мы употребляем понятие «весь» в собирательном смысле, потому что мы говорим о флоте, взятом в целом. Отдельные корабли могут не погибнуть, но флот как известное целое перестаёт существовать. Если мы употребляем выражение «все рабочие утомились», то в нём слово «все» употребляется в разделительном смысле, потому что мы имеем в виду утомление каждого рабочего в отдельности. Абстрактные и конкретные термины. Абстрактные термины—это такие термины, которые служат для обозначения качеств или свойств, состояний, действия вещей. Они обозначают качества, которые рассматриваются сами по себе, без вещей. Когда мы употребляем абстрактные термины, то мы совсем не имеем в виду обозначить, что соответствующие этим терминам.качества или свойства, состояния вещей существуют где-нибудь в определённом пространстве или в определённый момент времени, а, наоборот, они мыслятся нами без вещей, а потому и без определённого пространства и времени. Примером абстрактных терминов могут служить такие термины, как «тяжесть», «объём», «форма», «цвет», «интенсивность», «твёрдость», «приятность», «вес», «гуманность». В самом деле, «тяжесть» не есть что-нибудь такое, что имеет существование в данный момент времени: она существует не только в каком-нибудь определённом месте, но и везде, где только есть тяжёлые вещи. Абстрактными эти термины называются потому, что свойства или качества, обозначаемые ими, могут мыслиться без тех вещей, к которым они принадлежат: мы можем абстрагироваться, отвлекаться (abstrahere) от тех или иных вещей. Абстрактными, в отличном от этого смысле, иногда называются также и понятия таких вещей, которые не могут восприниматься нами как известная определённая вещь, например «вселенная», «звёздная система», «тысячеугольник», «человечество» и т. п. Конкретными являются понятия вещей, предметов, лиц, фактов, событий, состояний, сознания, если мы рассматриваем их имеющими определённое существование, например «квадрат», «пламя», «дом», «сражение», «страх» (1) и т. п. Отношение между абстрактными понятиями и конкретными следующее. Абстрактное.понятие получается из конкретного; мы путём анализа выделяем какое-нибудь качество, или свойство, вещи, например белизну из мела. С другой стороны, на конкретное понятие можно смотреть как на синтез абстрактно мыслимых качеств. Например, понятие «камень» представляет собой синтез качеств «тяжесть», «шероховатость», «твёрдость» и т. п. Надо заметить, что прилагательные всегда являются терминами конкретными, а не абстрактными; употребляя прилагательное «белый», мы всегда мыслим вещь; свойство же или качество мы мыслим в том случае, когда мы употребляем существительное «белизна». В языке иногда абстрактные и конкретные термины употребляются попарно. Например, конкретному термину «белый» соответствует абстрактное понятие «белизна», конкретному термину «строгий» соответствует абстрактное понятие «строгость», термину «квадрат» — «квадратность», «человек» — «человечность». Термины положительные и отрицательные. Положительные термины характеризуются тем, что они служат для обозначения наличности того или другого качества. Например, употребляя термины «красивый», «делимый», «конечный», мы хотим указать, что в предметах имеются налицо качества, обозначаемые этими словами; соответствующие же им отрицательные термины «некрасивый», «неделимый», «бесконечный» будут означать, что указанные качества отсутствуют в предметах. Другие примеры отрицательных терминов: «вневременный», «сверхчувственный», «ненормальный», «беспечный», «бессмысленный». Относительные и абсолютные термины. Есть, наконец, термины относительные и абсолютные. Что значит вообще абсолютный?. Под абсолютным мы понимаем то, что не находится в связи с чем-либо другим, что не зависит от чего-либо другого; под относительным мы понимаем то, что приводится в связь с чем-нибудь 1.О чувстве страха можно сказать, что оно имеет известное качество, например известную силу, или интенсивность, что оно обладает свойством парализовать умственную деятельность и т. д. Словом, оно может быть рассматриваемо как нечто, состоящее из совокупности свойств, или качеств.
другим; Абсолютный термин - это такой термин, который в своём значении не содержит никакого отношения к чему-либо другому, он не принуждает нас мыслить о каких-либо других вещах, кроме тех, которые он обозначает. Например, термин «дом» есть термин абсолютный. Мысля о доме, мы можем не думать ни о чём другом. Относительный же термин — это такой термин, который кроме того предмета, который он означает, предполагает существование также и другого предмета. Например, термин «родители» необходимо предполагает существование детей: нельзя мыслить о родителях без того, чтобы в то же время не мыслить о детях. Если мы говорим о каком-либо человеке, что он строгий, то мы наше внимание можем ограничить только этим человеком; но если мы говорим о нём, как о друге, то мы должны подумать ещё об одном лице, которое стоит к нему в отношении дружбы. Другие примеры: «компаньон», «партнёр», «сходный», «равный», «близкий», «король—подданные», «причина — действие», «северный — южный». Каждый из такой пары терминов называется соотносительным другому термину. Вопросы для повторения Какое существует соотношение между рассмотрением терминов и понятий? Какие термины общие и какие индивидуальные? О каких терминах мы говорим, что они употреблены в собирательном смысле, и о каких — в разделительном смысле? Какое различие между собирательными терминами и общими? Какие термины называются абстрактными и какие конкретными? Какие термины называются положительными и какие отрицательными? Какие термины относительные и абсолютные?
Глава III СОДЕРЖАНИЕ И ОБЪЁМ ПОНЯТИЙ Признаки понятий. Понятия в психологии получаются из сравнений сходных представлений. Представления в свою очередь складываются из отдельных элементов. Составные элементы представления или понятия принято называть признаками. Признаки есть то, чем одно представление или понятие отличается от другого. Например, признаками золота мы считаем «металл», «драгоценный», «имеющий определённый удельный вес» и т. п. Это всё то, чем золото отличается от других вещей, от не-металлов, от недрагоценных металлов и т. п. Не все признаки нужно считать равноценными. Каждое понятие имеет множество различных признаков, но при мышлении о нём мы прежде всего по преимуществу мыслим только известные признаки. Эти признаки являются как бы основными, около которых группируются другие признаки. Первые признаки называются сущственными, или основными, а остальные — второстепенными. Основные признаки — это такие признаки, без которых мы не можем мыслить известного понятия и которые излагают природу предмета. Например, для ромба существенным является тот признак, что он есть четырёхугольник с параллельными и равными сторонами и т. п.; несущественным для понятия ромба является тот признак, что он имеет ту или другую величину сторон, ту или другую величину углов. Признаки понятийсо времени Аристотеля принято делить на следующие 5 классов: Родовой признак. Если мы скажем, что химия есть наука, то наука будет родовым признаком для понятия «химия»; в числе других признаков, присущих понятию «химия», есть и признак «наука»; этот признак отличает химиюот всего, что не есть наука.Род (genus)или родовой признак есть понятие класса, в который мы вводим другое рассматриваемое нами понятие. 2. Видовое различие. Если мы скажем, что химия есть наука, занимающаяся изучением строения вещества, то прибавление признака — «занимающаяся изучением строения вещества» будет служить для обозначения того, чем эта наука отличается от других наук. Такой признак, который служит для того, чтобы выделять понятие из ряда ему подобных понятий, называется видовым различием (differentia specifica). Возьмём понятия «моряк русский», «моряк французский», «моряк английский». В этом случае «русский», «французский», «английский» есть видовое различие; оно служит для того, чтобы выделить моряка одной нации от моряков всех прочих наций. 3. Вид (species). Если к родовому признаку присоединить видовое различие, то получится вид. Например, «здание для склада оружия» == арсенал; «здание для склада хлеба» = амбар. В этом случае «здание» есть род, «для хранения оружия» есть видовое различие; присоединение к роду видового различия даёт вид «арсенал». Присоединение к понятию «здание» видового признака «служащее для хранения хлеба» даёт вид «амбар». Вид может быть Признаком, потому что его можно приписать понято. Например, «эта наука есть химия». 4. Собственный признак (proprium). Собственный признак — это такой признак, который присущ всем вещам данного класса, который не содержится в числе существенных признаков, но который может быть выведен из них. Например, существенным признаком человека является его «разумность». Из этого свойства вытекает его способность владеть речью. Этот последний признак есть собственный признак. Основной признак треугольника — это прямолинейная плоская фигура с тремя сторонами. Что же касается того признака треугольника, что сумма углов его равняется двум прямым, то это есть его собственный признак, потому что вытекает или выводится из основных признаков.» Мы этого признака не мыслим, когда думаем о треугольнике, поэтому он является выводным. 5. Несобственный признак (accidens). Несобственный пригнан — это такой признак, который не может быть выведен из существенного признака, хотя и может быть присущ всем вещам данного класса. Например, чёрный цвет ворона есть accidens. Если бы чёрный цвет ворона был выводим из основных свойств то, то он мог бы быть назван proprium, но он не выводим, так как бы не знаем, по какой причине вороны имеют чёрный цвет юрьев. Он есть, следовательно, accidens. Несобственные признаки делятся на две группы: на неотделимые несобственные признаки (accidens inseparable) и отделимые несобственные признаки (accidens separabile). Последние суть те признаки, которые присущи только некоторым вещам того или другого класса, но не всем, а первые присущи всем вещам данного класса. Например, чёрный цвет ворона есть accidens inseparabile. Чёрный цвет волос для человека есть accidens separabile, потому что есть люди, которые не имеют чёрного цвета волос. По отношению к отдельным индивидуумам несобственный признак также может быть отделимым и неотделимым. Отделимые — это такие признаки, которые одно время имеются налицо, а в другое время не имеются. Например, Бальфур—первый министр Англии. Через некоторое время он может не быть первым министром. Это есть признак отделимый. «Лев Толстой родился в Ясной Поляне». В этом предложении признак «родился в Ясной Поляне» есть неотделимый признак. Содержание и объём понятий. Понятия могут быть рассматриваемы с точки зрения содержания и объёма.
Рис. 2. Содержание понятия—это то, что мыслится в понятии. Например, в понятии «сахар» мыслятся признаки: сладкий, белый, шероховатый, имеющий тяжесть и т. д.; эти признаки в совокупности и составляют содержание понятия «сахар». Содержание понятия, другими словами, есть сумма признаков его; поэтому каждое понятие можно разложить на ряд присущих ему признаков. Содержание понятия может быть весьма изменчивым в зависимости от принятой точки зрения, от размера знания и т. п. Например, в понятии «сахар» химик мыслит одно содержание, а нехимик— другое. Объём понятия есть то, что мыслится посредством понятия, т. е. объём понятия есть сумма тех классов, групп, родов, видов и т.п., к которым данное понятие может быть приложено. Например, объём понятия «животное»: птица, рыба, насекомое, человек и т. д.; объем понятия «элемент»: кислород, водород, углерод, азот и т. д.; объём понятия «четырёхугольник»: квадрат, прямоугольник, ромб, трапеция; Таким образом, различие между объёмом понятия и содержанием понятия сводится к следующему: объём понятия означает ту совокупность предметов, к которым должно прилагаться данное понятие, а содержание обозначает те признаки, которые приписываются тому или другому понятию. Для более ясного представления объёма понятий и отношения объёмов существует особый приём, называемый «логической символикой».
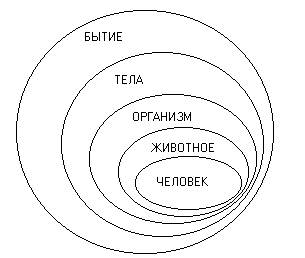
На рис. 1 большой круг символизирует собой понятие «элемент», а меньшие круги, в нём находящиеся, символизируют понятия, входящие в его объём. Если мы изображаем какой-нибудь круг внутри другого круга, то мы этим символизируем, что объём одного понятия входит в объём другого. Из рис. 2 видно, что понятие «дерево» содержит в своём объёме понятия «дуб», «ель» и т. п. Отдельные точки в круге «ель» символизируют индивидуальные, или единичные, ели. Понятие с большим объёмом называется родом по отношению к тому понятию с меньшим объёмом, которое входит в его объём. Понятие с меньшим объёмом в этом' случае называется видом. Понятия с большим объёмом можно назвать также понятиями более широкими или более общими. Любой вид может сделаться родом. Например, понятие «пальма» относится к понятию «дерево», как вид к роду, но в свою очередь оно относится уже как род к своим видам — «пальма кокосовая», «пальма фиговая» и т. д. Вообще более общее понятие есть род для менее общего понятия; более общее понятие представляет собой родовое понятие для менее общего, менее общее само становится родом для ещё менее общего и т. д., пока мы не придём к такому понятию, которое уже не может в своём объёме содержать какие-либо другие виды, а может подразделяться только на отдельные индивидуумы.
Рис. 3.
Рис. 3 а.
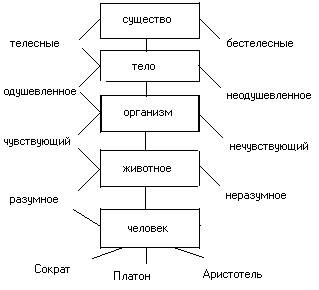
Следует упомянуть о попытке греческого философа Порфирия (233—304) при помощи схемы облегчить понимание от--ношения между охватывающими друг друга понятиями, т. е. понятиями, из которых одно входит в объём другого. Эта схема называется «деревом Порфирия». В понятие «бытия» (т. е. того, что вообще существует) входит понятие «телесного бытия» и «бестелесного бытия». Тело содержит в своём объёме одушевлённое тело, или организм, и неодушевлённое тело. Понятие «организм» содержит в своём объёме чувствующие и нечувствующие организмы (растения). Чувствующие организмы содержат в своём объёме разумные и неразумные существа и т. д. (рис. 3). Бытие есть высший род, который уже не может быть видом для другого рода. Такой род называется summum genus; человек — это низший вид. В его объём уже не входят понятия с меньшим объёмом, а входят только отдельные индивидуумы. Такое понятие называется infima species (самый низший вид). Ближайший высший класс (или род) того или другого вида называется proximum genus (ближайший род). Отношение между более широкими и узкими понятиями можно изобразить и иначе, именно, поместив круги, служащие для обозначения понятий с меньшим объёмом, внутри кругов, служащих для обозначения понятий с большим объёмом (рис. За). Ограничение и обобщение. Процесс образования менее общих понятий из более общих называется ограничением (determlnatio). Для образования менее общего понятия мы должны к более общему прибавить несколько признаков, благодаря чему понятие уясняется (determinatur). Например, чтобы из понятия «дерево» получить менее общее понятие «пальма», надо к признакам дерева прибавить специальные признаки пальмы: вид её листьев, прямизну ствола и т. д. Обратный процесс образования более общего понятия из менее общего, при котором, наоборот, некоторое количество признаков от данного понятия отнимается, называется обобщением (generalisatio). Род образуется из видов при помощи процесса обобщения, и, наоборот, виды образуются из родов при помощи процесса ограничения. Эти процессы мы можем изобразить при помощи следующей схемы:
Предположим, что у нас есть понятие А (наука). Из него при помощи видового различия а мы можем образовать вид Аа (математика); прибавив к понятию Аа видовое различие B (определение пространственных отношений), получим геометрию АаЬ. Прибавив к этому виду признак с (определение пространственных отношений на плоскости), получим планиметрию АаЬс. Обратный процесс — получение более общих понятий путём отбрасывания отдельных признаков — будет называться обобщением. И тот и другой процесс можно изобразить при помощи следующей схемы, в которой стрелки показывают или нисхождение от более общих понятий к менее общим или, наоборот, восхождение от менее общих к более общим понятиям. Отношение между объёмом и содержанием понятия. Для того чтобы ответить на вопрос, какое существует отношение между объёмом и содержанием понятия, возьмём какой-нибудь пример. Объём понятия «человек» обширнее, чем, например, объём понятия «негр». Употребляя понятие «человек», мы думаем обо всех людях, мы думаем о людях, живущих во всех пяти частях света, между прочим и в Африке. Употребляя понятие «негр», мы думаем только о тех людях, которые живу
|


 Рис. 1.
Рис. 1.