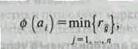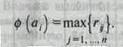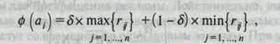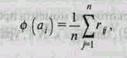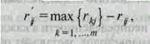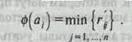Модель рекламной кампании

 

Фирма начинает рекламировать новый товар или услугу. Естественно, прибыль от будущих продаж должна значительно покрывать издержки на рекламную кампанию. При этом вначале расходы могут превышать прибыль, поскольку лишь малая часть потенциальных покупателей будет информирована о новинке. Затем, при увеличении числа продаж, появляется возможность рассчитывать на заметную прибыль. Наконец, наступит момент, когда рынок насытится, и рекламировать товар далее станет бессмысленно.

Рассмотрим обозначенные три этапа рекламной кампании в рамках следующей модели.

Пусть t — время, прошедшее с начала рекламной кампании;

N ₀ — общее число потенциальных платежеспособных покупателей;

N_t — число уже информированных потребителей, готовых купить рекламируемый товар;

α ₁ (t) - величина, характеризующая интенсивность рекламной кампании и фактически определяемая затратами на рекламу в данный момент времени.

Предполагается, что величина — скорость изменения со временем числа потребителей, узнавших о товаре и готовых купить его, - пропорциональна числу покупателей, еще не знающих о нем, т.е. величине

Прибыль превосходит издержки при условии pN ₀> 1, и если реклама действенна и недорога, а рынок достаточно емок, то выигрыш достигается с первых же шагов рекламной кампании (в действительности между оплатой рекламы, рекламными действиями и последующей покупкой имеет место временной лаг). При не слишком эффективной или дорогой рекламе фирма на первых порах несет убытки. Однако это обстоятельство не может служить основанием для прекращения рекламы. Действительно, выражение (3) и полученное с его помощью условие pN ₀ > 1 справедливы лишь при малых значениях N(t), когда функции P и S растут со временем по одинаковым законам. При увеличении N(t) опущенные в (1) члены второго порядка малости становятся заметными, в частности усиливается действие косвенной рекламы. Поэтому функция N(t) может стать более «быстрой» функцией времени, чем рассчитанная по формулам (2) и (3). Этот нелинейный эффект в изменении величины N(t) при неизменном темпе роста издержек позволяет скомпенсировать финансовую неудачу начальной стадии кампании.

Поясним данное утверждение в частном случае решения уравнения (1) с постоянными коэффициентами α ₁ и α ₂. Заменой = + N оно сводится к уравнению

 

Его решение стремится к предельному значению ₀, а функция N(t) — к N ₀. В единицу времени появляется ничтожно малое число новых покупателей, и поступающая прибыль при любых условиях не может покрыть продолжающихся издержек.

Рассмотренные задачи по использованию отдельных моделей в различных ситуациях еще не являются объемными и самодостаточными в сложных ситуациях управления маркетингом.

Понимание наличия риска и неопределенности в каждой конкретной ситуации, с которой сталкивается управленец-маркетолог, заставляет обратить внимание на вопросы, связанные с критериальностью определения риска.

Различают несколько критериев, по которым могут приниматься решения в условиях неопределенности с применением математических методов.

I. Критерий минимакса оценивает альтернативы, учитывая исключительно наихудший из всех возможных исходов, принимается та альтернатива, которая ведет в случае наихудшего исхода к наилучшему результату:

 

 

где ф (а_i) - значение критерия для i -й альтернативы, r_ij — исход при выборе i -й альтернативы и наступлении j -го варианта обстановки.

Это самый пессимистический критерий, следовательно, его скорее будет применять инвестор, стремящийся избегать малейшего риска.

II. Критерий максимакса представляет собой полную противоположность критерию минимакса - принимается та альтернатива, которая ведет в случае наилучшего исхода к наилучшему результату:

 

 

Очевидно, что критерий максимакса будет использовать инвестор, склонный к максимальному, часто неоправданному риску.

III. Критерий Гурвича представляет собой комбинацию критериев минимакса и максимакса и предусматривает применение коэффициента, определяющего, какой вес придается самому благоприятному и соответственно самому неблагоприятному исходу той или иной альтернативы при ее сравнении с другими альтернативами:

 

 

где δ - коэффициент критерия Гурвича (1 > δ > 0).

IV. Критерий Лапласа предполагает, что все варианты экономического процесса имеют одинаковую вероятность наступления. Учитывая это предположение, рассчитывается не что иное, как математическое ожидание случайной величины r_ij:

 

где n - количество вариантов процесса.

V. Критерий Сэвиджа позволяет минимизировать возможные потери после реализации ошибочной альтернативы в случае наступления неблагоприятного для этой альтернативы варианта событий. Эти потери измеряются как разница между полученным результатом и результатом, который мог бы быть получен в случае выбора альтернативы с наиболее благоприятным результатом в условиях наступившего варианта событий. Для использования этого критерия необходима трансформация исходной матрицы R в R':

 

 

где r’_ij — это упущенная прибыль. Расчет критерия Сэвиджа происходит по формуле

 

 

Пример выбора альтернативы с использованием различных критериев представлен в табл. 3.11.

 

Таблица 3.11