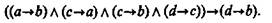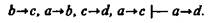СЛОЖНЫЕ И СЛОЖНОСОКРАЩЕННЫЕ СИЛЛОГИЗМЫ (ПОЛИСИЛЛОГИЗМЫ, СОРИТЫ, ЭПИХЕЙРЕМА)
Полисиллогизмом (сложным силлогизмом) называются два или несколько простых категорических силлогизмов, связанных друг с другом таким образом, что заключение одного из них становится посылкой другого. Различают прогрессивные и регрессивные полисиллогизмы. В прогрессивном полисиллогизме заключение предшествующего силлогизма становится большей посылкой последующего силлогизма. Приведем пример прогрессивного полисиллогизма, представляющего собой цепь из трех силлогизмов и имеющего такую схему:
Возьмем полисиллогизм, состоящий из двух силлогизмов, и справа запишем его схему.
Разъясним получение схемы 2. Если общие категорические суждения заменить совпадающими с ними по смыслу условными суждениями, то второй полисиллогизм примет следующий вид: Если предмет есть металл, то он теплопроводен. Если предмет есть щелочноземельный металл, то он, конечно, металл. Если предмет есть щелочноземельный металл, то он теплопроводен. Если предмет есть кальций, то он щелочноземельный металл. Значит, если предмет есть кальций, то он теплопроводен. Выразив суждение «Предмет есть металл» буквой а, суждение «Предмет теплопроводен» — буквой b, суждение «Предмет есть щелочноземельный металл» — буквой с, суждение «Предмет есть кальций» — буквой d, мы получим схему 2.В виде правила вывода схему 2 данного прогрессивного полисиллогизма можно записать так:
где Это правило вывода путем преобразований можно перевести в формулу алгебры логики:
Эта формула тождественно-истинна, если все посылки полисиллогизма являются общими суждениями. Регрессивный полисиллогизм — это такой сложный силлогизм, в котором заключение предшествующего силлогизма становится меньшей посылкой последующего силлогизма.
1. Всеорганизмы (В) суть тела (С). 2. Все тела (С) имеют вес (D). Все растения (А) суть организмы (B) Все растения (А) суть тела (С). _____________________ _____________________ Все растения (А) суть тела (С). Все растения (А) имеют вес (D).
Запишем эти два силлогизма схематически: 1. Все В суть С. 2. Все С суть D. Все А суть В. Все А суть С. _______________ ____________ Все А суть С. Все А суть D.
Соединив их вместе и не повторяя дважды суждение «Все А суть С», мы получим схемы регрессивного полисиллогизма для общеутвердительных посылок:
В виде правила вывода последнюю схему можно записать так:
Это правило вывода путем преобразования можно перевести в формулу алгебры логики:
Сорит (с общими посылками) Прогрессивный и регрессивный полисиллогизмы в мышлении чаще всего применяются в сокращенной форме — в виде соритов. Все растения (А) суть организмы (В). Все организмы (В) суть тела (С). Все тела (С) имеют вес (D). ______________________ Всякое растение (А) имеет вес (D).
Схема регрессивного сорита: Все А суть В. a -> b Все В суть С. b -> c Все С суть D. c -> d ___________ _____________ все А суть D. a -> d
Существуют два вида соритов: прогрессивный и регрессивный. Прогрессивный сорит получается из прогрессивного полисиллогизма путем выбрасывания заключений предшествующих силлогизмов и больших посылок последующих.
Все, что укрепляет здоровье (А), полезно (В). Спорт (С) укрепляет здоровье (А). Легкая атлетика (D) — спорт (C). Бег (Е) — вид легкой атлетики (D). _________________________ Бег (E) полезен (В).
Схемы прогрессивного сорита: Все А суть В. a -> b Все С суть А. c -> a Все D суть C. d -> c Все Eсуть D. e-> d ____________ ____________ Все E суть B. e -> b
Прогрессивный сорит начинается с посылки, содержащей предикат заключения, и заканчивается посылкой, содержащей субъект заключения. В виде правила вывода последнюю схему можно записать так:
Это правило вывода путем преобразований можно перевести в формулу алгебры логики:
Регрессивный сорит получается из регрессивного полисиллогизма путем выбрасывания заключений предшествующих силлогизмов и меньших посылок последующих. В первом категорическом силлогизме меняем местами посылки. Регрессивный сорит начинается с посылки, содержащей субъект заключения, и кончается посылкой, содержащей предикат заключения. В виде правила вывода последнюю схему можно записать так:
Это правило вывода путем преобразований можно перевести в формулу алгебры логики:
Эго формула алгебры логики (или исчисления высказываний), соответствующая регрессивному сориту, состоящему из трех общеутвердительных посылок.
|




 — знак вывода.
— знак вывода.