Логика в средние века
Средневековая логика (VI—XV вв.) изучена еще недостаточно. В средние века теоретический поиск в логике развернулся главным образом по проблеме истолкования природы общих понятий. Так называемые реалисты, продолжая идеалистическую линию Платона, считали, что общие понятия существуют реально, вне и независимо от единичных вещей. Номиналисты же, напротив, считали, что реально существуют только единичные предметы, а общие понятия — лишь имена, названия для них. Оба взгляда были неправильными, однако номинализм был ближе к материализму. Сформулируем основные проблемы, которые разрабатывались в средневековой логике: проблемы модальной логики, анализ выделяющих и исключающих суждений, теория логического следования, теория семантических парадоксов (логики в средние века усиленно занимались их анализом, например парадокса «Лжец» и др., и предлагали разнообразные решения). Теоретические источники средневековой арабоязычной логики следует искать в логике Аристотеля. Основателем арабоязычной логики считается сирийский математик аль-Фараби (870—950), который прокомментировал весь аристотелевский «Органон». Логика аль-Фараби направлена на анализ научного мышления. Им исследуются и вопросы теории познания, и грамматики. У него, как и у Аристотеля, метод мышления соотносится с реальными отношениями и связями бытия. Аристотель был «духовным наставником» аль-Фараби в области логики. Аль-Фараби выделяет в логике две ступени: первая охватывает представления и понятия, вторая — теорию суждений, выводов и доказательств. Сирийская логика послужила посредником между античной и арабоязычной наукой. Историки логики признают влияние логики арабов на развитие европейской логики в средние века. Таджик Ибн Сина (Авиценна; 980—1037) комментирует Аристотеля и сам пытается развить логику. Авиценне известна зависимость между категорическими и условными суждениями, выражение импликации через дизъюнкцию и отрицание, т. е. формула Трактат по логике впервые появился в России в X в. Это был перевод философской главы из «Диалектики» византийского писателя VII в. Иоанна Дамаскина, представлявшей собой изложение работ Аристотеля и его комментаторов. Первое систематическое учебное пособие по логике, включавшее аристотелевскую логику и отдельные идеи Гоббса, было подготовлено во второй половине XVII в. Тогда же в России начали распространяться отдельные идеи математической логики. В XVIII в. в России появляются оригинальные логические работы. Первых результатов добивается русский ученый-естествоиспытатель мирового значения Михаил Васильевич Ломоносов (1711—1765). Он вносит существенные изменения в традиционную силлогистику, предлагая свою классификацию умозаключений, отграничивает суждение от грамматического предложения и др. Дмитрий Сергеевич Аничков (1733—1788) в трактате «Заметки по логике» (Annotationes in logicam, metaphysicam et cosmologiam) исследовал модальные суждения, подразделяя их на четыре вида: необходимые, невозможные, возможные и не невозможные, сформулировал систему правил для ведения диспутов. Философ-материалист Александр Николаевич Радищев (1749—1802) одним из первых в мировой литературе поставил проблему необходимости логического анализа отношений, которого нет ни в логике Аристотеля, ни в логике средневековых схоластов. Он считал, что суждения представляют сравнение двух понятий или в суждениях выражено познание отношений, существующих между вещами. А. Н. Радищев дает следующую классификацию умозаключений11: 1) «рассуждение» (т. е. силлогизм); 2) «уравнение», т. е. умозаключения равенства, основанные на следующей аксиоме: равные и одинаковые вещи состоят в равном либо одинаковом союзе или отношении; 3) «умозаключения по сходству». Крупнейшими русскими логиками XIX в. в России были Михаил Иванович Каринский (1840—1917) и его ученик Леонид Васильевич Рутковский (1859—1920), основные логические работы которых посвящены классификации умозаключений. Основной замысел логической теории Каринского можно характеризовать как стремление построить аксиоматике -дедуктивную систему логики, исходя из основного отношения равенства (т. е. «тождества»), и в ней описать дедуктивные и индуктивные умозаключения, не используя элементов строгой формализации. Каринский в этой концепции примыкает к идеям Джевонса, что отметили уже его современники. Структура умозаключения, по Каринскому, такая. Из двух посылок, имеющих структуру (1) и (2), делается заключение (3).
А находится в отношении R к В: (1) В тождествен с С. (2) __________________________________ А находится в отношении R к С. (3)
Приведем примеры.
Москва находится восточнее Парижа. Париж — столица Франции. _____________________________________ Москва находится восточнее столицы Франции.
Самара находится западнее озера Байкал. Озеро Байкал — самое глубокое озеро мира. _________________________________________ Самара находится западнее самого глубокого озера мира.
Все выводы М. И. Каринский делит на две большие группы: 1) выводы, основанные на «сличении субъектов» и 2) выводы, основанные на «сличении предикатов» (при этом смысл терминов «субъект» и «предикат» не совпадает с соответствующим им традиционным пониманием). Основанием выводов является тождество (или соответственно различие) «субъектов» или «предикатов». В эти две большие группы, по мнению Карийского, можно отнести все виды умозаключений и, кроме них, еще и гипотезу. Исследуя работы по логике М. И. Каринского, историк логики Н. И. Стяжкин отмечал, что Каринский стремился охватить в своей классификации все виды умозаключений, встречающиеся в практике научного и общечеловеческого мышления. Но поставленная задача оказалась шире, чем принятые Каринским и положенные в основу его теории предпосылки. Она осталась невыполненной. Л. В. Рутковский — автор работы «Основные типы умозаключений» (1888). Если Каринский строил теорию выводов, используя лишь отношение тождества, и пытался свести к нему все другие отношения, то Рутковский считает возможным признать равноправными с отношением тождества и другие отношения, например отношения сходства, сосуществования и др. Так как существует многообразие отношений, имеется и многообразие видов логических выводов (т. е. видов умозаключений). Умозаключения делятся им на интенсивные (т. е. рассматриваемые в логике содержания) и экстенсивные (рассматриваемые в логике объема). Рутковский делит все выводы на две основные группы. Первая группа — выводы подлежащих (т. е. выводы по объему) — распадается на три вида: а) традукцию (выводы сходства, тождест-ва, условной зависимости); б) индукцию (полную и неполную); в) дедукцию (гипотетическую и негипотетическую). Вторая группа выводов — выводы сказуемых (по содержанию) — распадается на выводы «продукции» (разделительный силлогизм, выводы о совместности, современности предметов и др.), «субдукции» (выводы при классификациях и упорядочении предметов и др.), «эдукции» (отнесение предмета к виду его класса, заключения математической вероятности и др.). Аксиома «продукции» такова: «Из того, что предмет имеет признак В, следует, что этот же предмет имеет и признак С, так как признак В неизменно сосуществует с признаком С»12. Краткий анализ работ М. И. Каринского и Л. В. Рутковс-кого показывает, что их оригинальные работы по классификации видов умозаключений способствовали прогрессивному развитию традиционной логики в XIX в. Оригинальными были идеи казанского логика Николая Александровича Васильева (1880—1940). Они возникли в результате изучения проблем традиционной логики, но их значение было столь большим, что оказало влияние на развитие математической логики. Он вслед за другим русским логиком С. О. Шатуновским высказал идею о неуниверсальности закона исключенного третьего. Если Шатуновский пришел к этой идее в результате тщательного изучения особенностей математического доказательства применительно к бесконечным множествам, то Н. А. Васильев пришел к этому выводу в результате изучения частных суждений, рассматриваемых в традиционной логике. Основными работами Н. А. Васильева являются следующие: «О частных суждениях, о треугольнике противоположностей и о законе исключенного четвертого» (1910), «Воображаемая (неаристотелева) логика» (1912) и «Логика и металoгика». Н. А. Васильев подкреплял свои концепции формальной аналогией с неевклидовой геометрией Н. И. Лобачевского. Не все современники Васильева оценили его идеи, хотя некоторые из них считали, что он написал «остроумнейшую работу». Логические идеи Васильева можно рассматривать как некоторые предшествующие мысли, развитые далее в конструктивной и интуиционистской логиках, о неприменимости принципа исключенного третьего для бесконечных множеств. Васильев, кроме того, рассматривает условия, при которых представляется возможным оперировать с противоречивыми высказываниями внутри непротиворечивой логической системы. В XIX в. появляется математическая логика. Немецкий философ Г.В.Лейбниц (1646—1716) — величайший математик и крупный философ XVII в. — по праву считается ее основоположником. Лейбниц пытался создать универсальный язык, с помощью которого споры между людьми можно было бы разрешать посредством вычисления. При построении такого исчисления Лейбниц исходил из «основного принципа разума», который гласил, что во всех истинных предложениях, общих или частных, с необходимостью или случайно предикат содержится в субъекте. Он хотел всякому понятию дать числовую характеристику и установить такие правила оперирования с этими числами, которые позволили бы не только доказывать вообще все истины, доступные логическому доказательству, но и открывать новые. В надежде, что так люди смогут открывать новые истины, он видел особую заслугу своей всеобщей характеристики. Лейбниц говорил о ней как о чудесном общем языке, имеющем свой словарь (т. е. характеристические числа, отнесенные к понятиям) и свою грамматику (правила оперирования с этими числами). Лейбниц хотел построить арифметизированное логическое исчисление в виде некоторой вычисляющей машины (алгоритма). Однако этого ему сделать не удалось. В этой концепции Лейбница неприемлемо прежде всего то, что все содержание наших понятий якобы может быть выражено их характеристическими числами. Несостоятельным было представление Лейбница и о том, что человеческое мышление может быть полностью заменено вычисляющей машиной. Лейбниц полагал, что математику можно свести к логике, а логику считал априорной наукой. Сторонников такого обоснования математики называют логицистами — представителями субъективного идеалистического направления. Лейбниц является предшественником логицизма в том смысле, что он предложил сведение математики к логике и математизацию логики: построение самой логики как некоторой арифметики или буквенной алгебры. Но Лейбниц был предшественником логицизма и в том, что пытался создать арифметизированное логическое исчисление, о котором мы говорили. Покажем, как это делал Лейбниц. Возьмем такой категорический силлогизм:
+ 70, -33 +10, -3 Всякий мудрый есть благочестивый. + 70, -33 +8, -11 Некоторые мудрые есть богаты. _____________________________________ + 8, -11 +10, -3 Некоторые богатые есть благочестивы.
Сверху над понятиями написан выбранный наудачу правильный набор характеристических чисел для терминов посылок (мудрый, благочестивый, богатый). Истинность общеутвердительного суждения «Все S есть Р» (первая посылка) выражается тем, что обе характеристики субъекта делятся на соответствующие характеристики предиката, т. е. 70 (точно, без остатка) делится на 10, а —33 делится на —3, и числа, стоящие на диагоналях, взаимно простые, т. е. + 70 и — 3, так же как — 33 и +10, взаимно простые числа. Истинность частноутвердительного суждения, по Лейбницу, должна выражаться таким правилом: числа, стоящие на диагоналях, должны быть взаимно простыми, т. е. не иметь общих делителей, кроме единицы. Посылка «Некоторые мудрые — богаты» имеет такие числа:
т. е. на обеих диагоналях стоят взаимно простые числа. И заключение этому правилу также удовлетворяет, ибо на диагоналях стоят взаимно простые числа:
Истинность общеотрицательного суждения «Ни одно S не есть Р»у Лейбница выражалась тем, что по крайней мере на одной диагонали стоят не взаимно простые числа. Истинность частноотрицательного суждения выражалась тем, что по крайней мере одна из характеристик субъекта не делится на соответствующую характеристику предиката. Чтобы воспользоваться исчислением Лейбница, люди должны были свое рассуждение облечь в форму силлогизма и посмотреть, правильный он или неправильный. Однако построенная Лейбницем система удовлетворяла этому требованию только в применении к правильным, по Аристотелю, построенным силлогизмам. Автором настоящего пособия доказано, что все 19 правильных, по Аристотелю, модусов силлогизма окажутся правильными и по критерию Лейбница. Но в отношении неправильных модусов категорического силлогизма Аристотеля дело обстоит по-иному. Всегда можно построить такой пример, когда при разных правильных наборах числовых характеристик для посыпок получаются разные оценки заключения: в одних случаях оно оказывается истинным, в других — ложным. Исчисление Лейбница, таким образом, не выдержало проверки, что, конечно, заметил и сам Лейбниц, перешедший в дальнейшем к построению буквенного исчисления по образцу алгебры. Но тоже неудачно. Однако в этих замыслах Лейбница не все было порочным. Сам по себе метод арифметизации в математической логике играет весьма существенную роль как вспомогательный прием. В нем состоит, например, сущность метода, с помощью которого известный австрийский математик и логик К. Гёдель доказал неосуществимость Лейбницевой мечты о создании такой всеобщей характеристики, которая позволит заменить все человеческое мышление вычислениями. Ложной была именно метафизическая идея Лейбница о сведении всего человеческого мышления к некоторому математическому исчислению. Поэтому были ложны и вытекающие из нее следствия. Интенсивное развитие математическая логика получила также в работах Д. Буля, Э. Шредера, С. Джевонса, П. С. Порецкого и других логиков. Английский логик Джордж Буль (1815—1864) разрабатывал алгебру логики — один из разделов математической логики. Предметом его изучения были классы (как объемы понятий), соотношения между ними и связанные с этим операции. Буль переносит на логику законы и правила алгебраических действий. В работе «Исследование законов мысли»13, которая оказала большое влияние на развитие логики, Буль ввел в логику классов в качестве основных операций сложение («+»), умножение («х» или возможен пропуск знака) и вычитание («—»). В исчислении классов сложение соответствует объединению классов, исключая их общую часть, а умножение — пересечению. Вычитание Буль рассматривал как действие, противоположное (opposite) сложению, — отделение части от целого, то, что в естественном языке выражается словом «кроме» (except). Буль ввел в свою систему логические равенства, которые он записывал посредством знака «=», соответствующего связке «есть». Суждение «Светила есть солнца и планеты» в виде равенства им записывается так: x = y + z, откуда следует, что x—z = y. Согласно Булю, в логике, как и в алгебре, можно переносить члены из одной части равенства в другую с обратным знаком. Буль открыл закон коммутативности для вычитания (х- у = - у+х)и закон дистрибутивности умножения относительно вычитания (z (χ —y) = zx—zy). Он сформулировал общее правило для вычитания: «Если от равных вычесть равные, то остатки будут равными. Из этого следует, что мы можем складывать или вычитать равенства и употреблять правило транспозиции точно так же, как в общей алгебре»14. Предметом исследования ученого были также высказывания (в традиционной логике их называют суждениями). В исчислении высказываний, по Булю, сложение («+») соответствует строгой дизъюнкции, а умножение («х» или пропуск знака) — конъюнкции. Чтобы высказывание записать в символической форме, Буль составляет логическое равенство. Если какой-либо из терминов высказывания не распределен, он вводит термин V для обозначения класса, неопределенного в некотором отношении. Для того чтобы выразить частноотрицательное суждение, например «Некоторые люди не являются благоразумными», Буль сначала представляет его в форме «Некоторые люди являются неблагоразумными)), а затем выражает в символах обычным способом. По Булю, существует три типа символического выражения суждений: X=VY (только предикат не распределен): Χ =V (оба термина — субъект и предикат — распределены); VX=VY (оба термина не распределены). Диалектика соотношения утверждения и отрицания в понятиях и суждениях у Буля такова: без отрицания не существует утверждения, и, наоборот, во всяком утверждении содержится отрицание. Утверждения и отрицания связаны с универсальным классом: «Сознание допускает существование универсума не априори, как факт, не зависящий от опыта, но либо апостериори, как дедукцию из опыта, либо гипотетически, как основание возможности утвердительного рассуждения»15. Различая живой разговорный язык и «язык» символический, Буль подчеркивал, что язык символов лишь вспомогательное средство для изучения человеческого мышления и его законов. Немецкий математик Эрнст Шрёдер (1841—1902) собрал и обобщил результаты Буля и его ближайших последователей. Он ввел в употребление термин «Logikkalkul» (логическое исчисление), новые по сравнению с Булем символы. В основу исчисления классов он положил не отношение равенства, как это было у Буля, а отношение включения класса в класс, которое обозначал как Пропуском знака Шрёдер обозначает операцию пересечения классов, например ab. Применительно к высказываниям формой α +b он обозначает нестрогую дизъюнкцию. Во взглядах Э. Шредера на отрицание можно отметить много интересного и нового по сравнению со взглядами Буля. Под отрицанием класса а Шрёдер понимает его дополнение до единицы16. Если классов больше двух, то Шредер оперировал с ними по сформулированным им правилам. Правило 1: если среди сомножителей некоторого произведения находятся такие, из которых один является отрицанием другого, то произведение «исчезает», т. е. равно 0. Например, abc х ab, cd, =0, так как имеется b и b 1. Правило 2: если среди членов некоторой суммы находится хотя бы один, который оказывается отрицанием другого, то вся сумма равна 1: a+b+c, +a+c+d, = l. Значительное внимание Шрёдер уделил анализу структуры отрицательных суждений. Он отрицательную частичку прилагает к предикату, т. е. вместо «А не есть В» он берет «А есть не-В». Так, суждение «Ни один лев не является травоядным», если следовать идеям Шредера, надо заменить на суждение «Все львы являются нетравоядными». Шрёдер класс а, как отрицание класса а считает очень неопределенным. И в доказательство этой мысли приводит такой пример. Понятие «несражающийся» (в армии) охватывает: саперов, полковых ремесленников, служащих лазарета, врачей, которые относятся к армии, но не сражаются. Опираясь на законы де Моргана, Шредер проводит анализ языка разговорной речи. Выражение Шредер формулирует правила, или требования, научной квалификации: 1) между родом и суммой его видов должно быть тождество; 2) все виды должны быть дизъюнктивными, т. е. должны исключать друг друга, и попарно в произведении давать 0; 3) для расчленения рода на виды должно быть одно основание. Используя отрицание, Шрёдер показал, как классифицируемый род делится на виды и подвиды. В логическом исчислении, доведенном до наибольшей простоты, Шрёдер признает три основных действия: сложение (трактуя его как нестрогую дизъюнкцию), умножение и отрицание. Однако вычитание он считает не безусловно выполнимой операцией. По нашему мнению, в логике классов вполне приемлема операция вычитания классов, но мы понимаем ее принципиально иначе, чем Буль и Шрёдер. Буль и Шрёдер считали, что в разности (а—b) b должно полностью входить в а, если же b > а или а и b несовместимы, то операция вычитания невыполнима. В отличие от Буля и Шрёдера мы допускаем возможной (т. е. выполнимой) разность всяких двух классов а и b, из которых b может и не быть частью а; в качестве следствий мы учитываем случаи вычитания, когда классы а и b являются пустыми или универсальными. Данный подход рассмотрен выше на с. 57—59. Наиболее известны работы английского логика Стенли Джевонса (1835—1882) «Principles of Science, a Treatise on Logic and Scientific Method» (London, 1874) и «Elementary Lessons in Logic, Deductive and Inductive» (London, 1870). В качестве логических операций он признавал конъюнкцию, нестрогую дизъюнкцию и отрицание и не признавал обратных логических операций — вычитания и деления. Джевонс обозначает классы буквами А, В, С... а их дополнение до универсального класса, обозначаемого 1, или их отрицания — соответственно курсивными буквами а, b, с... Нулевой (пустой) класс он обозначает 0, а связку в суждении заменяет знаком равенства. Джевонс большое значение придает принципу замещения или подстановки, который им формулируется так: если только существует одинаковость, тождество или сходство, то все, что верно об одной вещи, будет верно и о другой. Этот принцип замещения играет важную роль в умозаключении. Для обозначения отношения одинаковости или тождества Джевонс употребляет знак «=». Обозначив положительные и отрицательные термины соответственно через А и а, В и b, Джевонс записывает закон противоречия как Аа—0. Критерием ложности заключения, по Джевон-су, является наличие в нем противоречия, т. е. утверждения и отрицания одного и того же положения, что записывается, например, как наличие Аа, Вb, АВСа. С. Джевонс говорил, что утвердительные суждения можно представлять в отрицательной форме. Но он напрасно столь категорически заявлял, что имеются сильные основания в пользу того, чтобы употреблять все предложения в их утвердительной форме, а различие (т. е. отрицательные суждения) не способно быть основанием умозаключения. С. Джевонс не отрицал, что утверждение и отрицание, сходство и различие, равенство и неравенство представляют пары одинаково основных отношений, но утверждал, что умозаключение возможно только там, где прямо находится или подразумевается утверждение, сходство или равенство, словом, какой-нибудь вид тождества. Согласно законам диалектики, тождество и различие являются двумя сторонами единого предмета или процесса. Отражение отношений тождества и различия, имеющихся в самих предметах действительного мира, находит свое выражение и в мышлении, в формах умозаключений. Поэтому отбросить различие, выражающееся в отрицательных суждениях, и все свести только к тождеству, выражающемуся в утвердительных суждениях, нельзя, да и нет в этом необходимости. Единство противоположностей — тождества и различия — неразрывно. Интересны и оригинальны взгляды С. Джевонса на категорический силлогизм с двумя отрицательными посылками. Он утверждает, что его принцип умозаключения ясно отличает случаи, когда оно оказывается правильным или неправильным. Он приводит пример умозаключения.
Все, что не металлично, не способно к сильному магнитному влиянию. Уголь не металлнчен. __________________________________________________ Уголь не способен ж сильному магнитному влиянию.
Здесь из двух отрицательных посылок получается истинное отрицательное заключение. С. Джевонс считает, что там, где возможно подставлять тождественное вместо тождественного, возможен вывод заключения из двух отрицательных посылок. С. Джевонс внес значительный вклад в алгебру логики, особенно в проблему отрицания классов и отрицательных суждений. Следующий этап в развитии математической логики связан с именем русского логика, математика и астронома Платона Сергеевича Порецкого (1846—1907). Его работы17 существенно обобщают и развивают достижения Буля, Джевонса и Шрёдера. Анализируя понятия, Порецкий различает две формы: форму, обладающую данным признаком, обозначаемую буквами а, b, с..., и форму, им не обладающую, обозначаемую а 1, b 1, с 1и т. д.18 Формы совместного обладания или необладания несколькими признаками он записывает так: а, а 1 b, b 1(без особого знака между буквами). Современное пересечение классов Порецкий называет операцией реализирования (умножения), обозначая ее «·», а операцию объединения классов — абстрагированием (сложением), обозначая ее «?», т. е. знаком вопроса; 0 и 1 обозначают пустой класс и универсальный. Порецкий вводит операцию отрицания классов (отрицание а обозначается через а1) — это дополнение к классу а. Для каждого данного а его отрицание, т. е. а 1может быть различно. Это определяется избранным универсальным классом. Так, если за 1, т. е. универсум, принять англичан, а за а класс артистов, то а 1— англичане-ые-артисты, но если 1 обозначает класс людей, то а 1— людей-не-артистов и т. д. Заслуга Порецкого в том, что он рассматривал логические операции не только над отдельными логическими классами, но и над логическими равенствами. Порецкий считает, что если два класса состоят из одних и тех же предметов, т. е. имеют равные объемы и могут отличаться только формой, то они равны между собой. Соединяя равные классы знаком «=», мы получаем логическое равенство. Равенством логических классов русский логик называет полную их тождественность, т. е. одинаковость их логического содержания, считая, что все их различие может состоять только в способе их происхождения. Примером такого равенства является закон де Моргана: (m+ n)1 —m 1 n 1.Если классы а и b равны, то и их отрицания, т. е. классы а 1и b 1 , также равны. По его мнению, отрицание всякого равенства приводит к новому равенству, тождественному первоначальному. Операция отрицания над системами равенств, по мнению Порецкого, непригодна. К соединению двух и более равенств в одно новое равенство пригодны лишь две логические операции: сложение и умножение отдельных частей равенств, причем предварительно каждое отдельное равенство может быть в случае надобности заменено его отрицанием. В созданной им теории логики Порецкий подчеркивал взаимосвязь двух проблем: выведения следствия из заданной системы посылок и нахождения тех посылок, из которых данное логическое равенство может быть получено в качестве следствия. Несколько подробнее остановимся на методе нахождения всех простых следствий из данных посылок, который в теории логики получил название метода Порецкого — Блэйка (его предложил американский математик Блэйк19 на основе работы Порецкого). Простым следствием из данных посылок называется дизъюнкция каких-либо букв или их отрицаний, являющаяся логическим следствием из этих посылок, и притом таким, которое не поглощается никаким более сильным следствием такого же вида. (Мы говорим, что а сильнее b, если из а следует b, но из b не следует а.) Все простые следствия из данных посылок можно получить, выполнив преобразования следующих пяти типов: 1) привести конъюнкцию посылок к конъюнктивной нормальной форме (КНФ). КНФ есть конъюнкция из дизъюнкций элементарных высказываний или их отрицаний, эквивалентная данному выражению [т. е. если есть импликация, то се надо заменить на дизъюнкцию по формуле 2)произвести все операции «отбрасывания», т. е. члены вида 3)использовать законы выявления, т. е. формулы
4) произвести все «поглощения» на основании законов поглощения: 5) из всех повторяющихся членов оставить только один (на основании законов идемпотентности). В результате получится силлогистический многочлен, который будет содержать все простые следствия из данных посылок, и только простые следствия. Они интереснее, чем обычные логические следствия, так как зависят от меньшего числа параметров (элементарных высказываний). Покажем это на конкретной задаче. Из данных трех посылок, имеющих следующие формы: 1. Соединяем посылки знаками конъюнкции и приводим выражение к КНФ:
2. В полученной КНФ к членам 1 и 3 применяем закон выявления, получаем
Затем к членам 2 и 4 снова применяем этот же закон:
3. Производим операции «поглощения». Первый член (qr) поглощается четвертым (q), поэтому отбрасываем первый член, а второй член (pq) поглощается пятым членом (р). В результате этого получим
Вывод: при данных посылках суждения г и р истинны, а суждение q ложно, т. е. если суждениями выражены некоторые события, то событие г и событие ρ наступят, а событие q не наступит. Исследования Порецкого продолжают оказывать стимулирующее влияние на развитие алгебраических теорий логики и в наши дни. В XX в. математическая логика развивалась в трудах Ч. С. Пирса и Дж. Пеано. Американский логик Чарльз Сандерс Пирс (1839—1914) внес существенный вклад в разработку алгебро-логических концепций и явился основоположником новой науки — семиотики (общей теории знаков). В работах Пирса содержится тенденция к расчленению семиотики: на прагматику (анализирует отношение знака к его исследователю), семантику (выясняет отношение знака к обозначаемому им объекту) и синтактику (исследует взаимоотношения между знаками). Пирс пишет о том, что реальное можно определить как нечто, свойства которого независимы от того, что о них мыслят. Наиболее общим подразделением знаков он считал такие: изображения (icons), индексы (indices) и символы (symbols). Пирс предлагал классификацию знаков и по другим основаниям. Пирс предложил строить исчисление высказываний лишь на одной операции, этим предвосхитив результаты М. X. Шеффера (Шеффер также строил исчисление высказываний на одной операции, которая вошла в историю логики под именем ее создателя — штрих Шеффера). Единственной логической операцией Пирс предлагал считать отрицание нестрогой дизъюнкции. Пирсу принадлежит работа по логике «Studies in Logic» и др. Достижения Джузеппе Пеано (1858—1932), итальянского математика, явились переходным звеном от алгебры логики, в том виде, какой ей придали Буль, Шрёдер, Порецкий и Пирс, к современной форме математической логики. Основные результаты Пеано были опубликованы в пятитомном «Формуляре математики»21. Пеано ввел следующие употребляющиеся и выне символы: а) Крупным вкладом Пеано в развитие аксиоматического метода явилась его система из пяти аксиом для арифметики натуральных чисел. На базе своей аксиоматики Пеано строит всю теорию натуральных чисел. На заключительном этапе своей научной деятельности Пеано приступил к систематическому изложению логики как особой, по его мнению, математической дисциплины. Далее развитие математической логики осуществлялось по многим направлениям, а также в проблемном плане. Это было обусловлено необходимостью дальнейшего освоения как классической и неклассической логик, так и в связи свозникшими трудностями в обосновании математики.
|

 В учебнике «Логика» Ибн Сина стремился обобщить аристотелевскую силлогистику. Вначале Ибн Сина, П. С. Порецкий, Е. Л. Буницкий и др., внесли существенный вклад в развитие логики на уровне мировых логических концепций.
В учебнике «Логика» Ибн Сина стремился обобщить аристотелевскую силлогистику. Вначале Ибн Сина, П. С. Порецкий, Е. Л. Буницкий и др., внесли существенный вклад в развитие логики на уровне мировых логических концепций.

 Знак «+» Буль использовал для обозначения объединения классов, исключая их общую часть, т. е. симметрическую разность (см. рис. 8), а у Шрёдера знак «+» обозначает объединение классов без исключения их общей части (см. рис. 11).
Знак «+» Буль использовал для обозначения объединения классов, исключая их общую часть, т. е. симметрическую разность (см. рис. 8), а у Шрёдера знак «+» обозначает объединение классов без исключения их общей части (см. рис. 11). в речи означает, что «каждое с есть не-а и (одновременно) не-b».Для него можно выбрать другое выражение: «Каждое с не есть ни а, ни b». Это конъюнктивное суждение, примером которого может быть: «Каждая рыба — не птица и не млекопитающее». Другое суждение «Никакая рыба не есть птица и млекопитающее» означает в символическом виде
в речи означает, что «каждое с есть не-а и (одновременно) не-b».Для него можно выбрать другое выражение: «Каждое с не есть ни а, ни b». Это конъюнктивное суждение, примером которого может быть: «Каждая рыба — не птица и не млекопитающее». Другое суждение «Никакая рыба не есть птица и млекопитающее» означает в символическом виде  , что эквивалентно, на основании правила де Моргана,
, что эквивалентно, на основании правила де Моргана,  Так называемое отрицательное по связке суждение «ни а, ни b не есть с» представляется в виде
Так называемое отрицательное по связке суждение «ни а, ни b не есть с» представляется в виде 

 можно исключить, так как этот член тождественно истинен;
можно исключить, так как этот член тождественно истинен;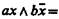


 — требуется вывести все разные (неэквивалентные между собой) формы простых логических следствий. Для решения задачи выполним следующие операции.
— требуется вывести все разные (неэквивалентные между собой) формы простых логических следствий. Для решения задачи выполним следующие операции. или, в другой записи,
или, в другой записи, 



 — знак принадлежности элемента к классу; б)
— знак принадлежности элемента к классу; б)  — знак включения одного класса в другой класс; в)
— знак включения одного класса в другой класс; в)  — знак объединения классов; г) — знах для обозначения операции пересечения классов.
— знак объединения классов; г) — знах для обозначения операции пересечения классов. 



