Решение. Построим эпюры изгибающих моментов от заданной нагрузки (рис
Построим эпюры изгибающих моментов от заданной нагрузки (рис. 4.25, а) и от единичных обобщенных сил, соответствующих искомым перемещениям (рис. 4.25, б, в). Разобьем эпюру моментов от заданной нагрузки на три треугольника и найдем их площади:
Для определения угла поворота сечения А перемножим эпюры М и М 1. Для этогонайдем ординаты на эпюре М 1, расположенные под центрами тяжести треугольников:
Тогда угол поворота сечения А согласно формуле (4.22)
Положительный знак угла поворота показывает, что поворот сечения А происходит по направлению обобщенной силы, то есть в соответствии с показанной на рис. 4.25, б единичной парой сил по ходу часовой стрелки. Результат совпадает с полученным ранее аналитическим способом. Чтобы найти прогиб сечения D, используем при перемножении эпюру М 2. Ординаты на эпюре М 2 под центрами тяжести треугольников будут такими:
Найдем прогиб сечения D по формуле (4.22):
Прогиб сечения D получился положительным. Это означает, что точка D перемещается по направлению единичной силы. Поскольку единичная сила показана на рис. 4.25, в направленной вниз, то и перемещение точки D происходит вниз. Полученный результат совпадает с тем, который был получен ранее аналитическим способом.
|

 кН·м2;
кН·м2;  кН·м2;
кН·м2;  кН·м2.
кН·м2. ;
;  ;
;  .
.
 .
. м;
м;  м;
м; 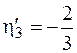 м.
м. 
 .
.


