Дифракция световых волн
Дифракцией называется огибание волной препятствий. Дифракция выражена достаточно сильно, если длина волны соизмерима с размерами препятствия. Возникновение дифракции можно объяснить с помощью принципа Гюйгенса: каждая точка, до которой доходит волновое движение, служит центром вторичных волн; огибающая этих волн дает положение фронта волны в следующий момент. Для количественной оценки результатов дифракции и нахождения амплитуды результирующей волны в любой точке пространства Френель дополнил принцип Гюйгенса представлением о когерентности вторичных волн и их интерференции. Различают: 1) дифракцию плоской волны – дифракцию Фраунгофера и 2) дифракцию сферической волны – дифракцию Френеля Расчеты с использованием принципа Гюйгенса – Френеля – чрезвычайно трудная задача. Поэтому для качественной оценки результатов дифракции Френель предложил разбивать фронт волны не на бесконечное множество точечных источников, а на конечное число зон. Зонами Френеля называются участки фронта волны, построенные таким образом, что расстояние от краев каждой зоны до точки наблюдения отличаются на l/2.
Построение зон для сферической волны, испущенной источником S, показано на рис. 9. Колебания, приходящие в точку наблюдения P от аналогичных точек двух соседних зон, будут находиться в противофазе. Поэтому и результирующие колебания, создаваемые каждой из зон в целом, будут для соседних зон отличаться по фазе на p. Радиус внешней границы k-ой зоны Френеля в этом случае
где а – расстояние от источника света до фронта волны, b – расстояние от точки наблюдения до вершины фронта волны О. Для плоской волны радиус находится как
Для качественной оценки результата дифракции на малом круглом отверстии достаточно найти количество зон Френеля, попавших в это отверстие. Если количество зон четное, то в точке Р будет минимум, если нечетное – максимум. Аналогично оценивается дифракция Фраунгофера на узкой щели (рис. 10). Открытая часть фронта волны, дошедшей до щели, разбивается на параллельные краям щели зоны Френеля шириной
Расстояние d между серединами соседних щелей называется постоянной или периодом решетки. При этом в направлениях, для которых разность хода волн от соседних щелей равна целому числу длин волн, будут наблюдаться максимумы интенсивности, называемые главными. Таким образом, условие главных максимумов имеет вид
dsinj = 2kl/2, k = 0, 1, 2... (55)
При этом интенсивность главных максимумов Imax пропорциональна интенсивности Ij, создаваемой в направлении j одной щелью. Imax = N2I, (56), где N – общее число щелей решетки. Дифракционная решетка служит спектральным прибором, разрешающая способность которого где Dl – наименьшая разность длин волн двух близких спектральных линий с длинами волн l и l+Dl, при которых они еще воспринимаются раздельно (разрешаются). Разрешающая способность дифракционной решетки может быть найдена по формуле R = kN, (58)
где k – порядок дифракционного спектра, N – общее число щелей решетки.
Поляризация световых волн
В естественном свете колебания различных направлений быстро и беспорядочно сменяют друг друга. Свет, в котором направления колебаний упорядочены каким-либо образом, называют поляризованным. Обычно ограничиваются рассмотрением плоскополяризованного света, то есть такого, в котором колебания светового вектора происходят только в одной плоскости. Плоскополяризованный свет получают из естественного с помощью приборов – поляризаторов. Эти приборы пропускают только колебания, параллельные плоскости, называемой плоскостью поляризатора. Если через поляризатор пропустить естественный свет с интенсивностью Iест, то интенсивность прошедшего поляризованного света
I = 0, 5Iест. (59) Если на поляризатор падает уже плоскополяризованный свет с амплитудой А0 и интенсивностью I0 (рис. 12), то сквозь прибор пройдет составляющая колебания с амплитудой А = А0 cos j, где j – угол между плоскостью колебаний падающего света и плоскостью поляризатора. Следовательно, интенсивность прошедшего света I определяется выражением
I = I0 cos2j (60)
Соотношение (60) носит название закона Малюса. Действие поляризаторов разных типов основано либо на явлении поляризации света при отражении его от диэлектрика, либо на поляризации при двойном лучепреломлении, которое наблюдается при прохождении света через анизотропные вещества (кристаллы).
В первом случае имеет место закон Брюстера, который гласит, что отраженный от диэлектрика свет будет полностью поляризован, если тангенс угла падения aБ равен относительному показателю преломления сред n21 = n2/n1 (рис. 13):
tgaБ = n21. (61)
Примеры решения задач
Решение а) Уравнение гармонического колебания имеет вид
uх = dx/dt = –xmwsin(wt + j). (2). Чтобы выразить проекцию скорости через координату, нужно исключить время из формул (1) и (2). Для этого возведем оба уравнения в квадрат, разделим первое на xm2, второе на xm2w2 и сложим: x2/xm2 + uх2/(xm2w2) = 1; w = 2pn Þ x2/xm2 + Vuх2/(xm24p2n2) = 1 Найдем выражение для проекции скорости точки uх2 = xm24p2n2(1 – x2/xm2) = 4p2n2(xm2– x2)
Знак плюс соответствует направлению вектора скорости, совпадающему с положительным направлением оси x, знак минус – с отрицательным. б) Проекцию силы, действующей на точку, найдем по второму закону Ньютона Fх = maх (3), где aх – проекция ускорения точки, которую можно получить, взяв производную по времени от проекции скорости: ах = duх/dt = –xmw2cos(wt + j) = –4p2n2xmcos(wt + j), Fх = – 4p2n2mxmcos(wt + j). Максимальное значение силы будет при cos(wt + j) = – 1 Þ Fmax = 4p2n2mxm, Fmax = 4× 3, 1420, 520, 005× 0, 03 = 1, 49 мН в) Полная энергия колеблющейся точки есть сумма кинетической и потенциальной энергий, вычисленных для любого момента времени. W = Wk + Wп. В соответствии с законом сохранения полной механической энергии в момент, когда кинетическая энергия достигает максимального значения, потенциальная энергия равна нулю. Поэтому полная энергия W колеблющейся точки равна максимальной кинетической энергии Wk max: W = Wk max = mu2max /2. (4) Максимальную скорость найдем из (2) при sin(wt + j) = –1; umax = 2pnxm. (5) Подставим (5) в (4): W = 2p2mn2xm2 W = 2× 3, 142× 0, 005× 0, 52× 0, 032 = 22, 1 мкДж.
Решение В данной задаче следует рассмотреть два случая. 1) Сопротивление среды уменьшает частоту свободных колебаний и приводит к их затуханию.
Решим первую задачу. Период затухающих колебаний может быть найден через циклическую частоту затухающих колебаний w:
где w0 – собственная циклическая частота, b – коэффициент затухания.
где l – логарифмический декремент затухания.
Выразим период колебаний: Закон убывания амплитуды затухающих колебаний: xm = xm(0)e-bt = xm(0)e-lt / T. По условию xm(0)/xm = h. Число колебаний N = t/T, где t – общее время колебаний, T – время одного колебания (период). xm(0)/xm = elN = h. Логарифмируя, получим l = ln(h)/N. (2) Подставим выражение (2) в (1): Во втором случае на гирю будет действовать вынуждающая сила, изменяющаяся по гармоническому закону: F = F0cos Wt. Тогда (с учетом отставания по фазе на j = 3p/4) гиря будет совершать установившиеся вынужденные колебания по закону x(t) = xmcos(wt – j). Амплитуда вынужденных колебаний
Добротность осциллятора
Сдвиг фаз между смещением и возмущающей силой зависит от соотношения между циклическими частотами вынужденных колебаний W и свободных незатухающих колебаний w0:
а) Длина волны может быть найдена через скорость ее распространения и период: l = uT; l = 15× 1, 2 = 18 м б) Уравнение волны для смещения колеблющейся точки: x = xmcos w(t – x/u), где х – расстояние точки от источника волн;
j = w(t– x/u) = 2p/t(t – x/u), j = 2× 3, 14/1, 2× (4 – 45/15) = 5, 24 рад = 300о. При этом смещение точки в момент t = 4 c x = 2× cos(2× 3, 14/1, 2)× (4 – 45/15) = 0, 01 м. Скорость точки находим взяв первую производную от смещения по времени:
Подставив численные значения, получим Ускорение есть первая производная от скорости по времени:
После вычислений в) Разность фаз Dj колебаний двух точек волны связана с расстоянием между ними Dх соотношением Dj = 2pDх/l=2p/l× (х2 – х1); Dj = 2× 3, 14/18× (30 – 20) = 3, 49 рад = 200о.
4. Колебательный контур состоит из конденсатора емкостью С = 5, 0 мкФ и катушки индуктивностью L = 0, 2 Гн. Определить максимальную силу тока I0 в контуре, если максимальная разность потенциалов на обкладках конденсатора Um = 90 В. Сопротивлением контура пренебречь. Какой будет добротность контура, если в него включить активное сопротивление R = 10 Ом?
Первую часть задачи можно решить двумя способами: путем исследования уравнений свободных электромагнитных колебаний и на основе закона сохранения энергии. 1 способ: При R = 0 в контуре будут незатухающие колебания:
Используя определение силы тока, продифференцируем обе части уравнения по времени: I = dq/dt = w0qmcos(w0t + j0), где Im = w0qm – амплитудное значение силы тока,
qm = CUm
2 способ: В процессе незатухающих электромагнитных колебаний полная электромагнитная энергия контура, равная сумме энергий электрического поля конденсатора CU2/2 и магнитного поля катушки LI2/2, остается постоянной. При этом в те моменты, когда конденсатор максимально заряжен (U = Um), сила тока равна нулю. Следовательно, полная энергия контура W = CUm2/2. В то время, когда конденсатор разряжен (U = 0), сила тока достигает максимального значения Im. Тогда полная энергия контура W = LIm2/2. CUm2/2 = LIm2/2 Þ При включении в колебательный контур активного сопротивления колебания в нем будут затухающими. Добротность контура может быть найдена через логарифмический декремент l: Q = p/l, l = bT, где b – коэффициент затухания, b = R/(2L), l = RT/(2L). Период колебаний находим по формуле Томсона:
5. Поток солнечной энергии на орбите Земли равен 1340 Вт/м2. Чему равны амплитуды Em и Hm плоской электромагнитной волны с такой средней плотностью потока энергии? Какое давление оказывает волна, которая падает по нормали на поверхность тела, полностью ее поглощающего? Решение
1) Плотность потока энергии, переносимой электромагнитной волной, определяется модулем вектора Пойнтинга. По определению,
S = EH, где E = Emcos(wt – kx) –мгновенное значение напряженности электрического поля волны, H = Hmcos(wt – kx) –мгновенное значение напряженности магнитного поля волны. w – циклическая частота, k = w/u – волновое число, Em и Hm – амплитуды напряженностей электрического и магнитного полей волны соответственно. Мгновенное значение модуля вектора Пойнтинга S = EmHmcos2(wt – kx), а его среднее за период T = 2p/w значение
< S> = 1/2EmHm (так как < cos2(wt – kx)> = 1/2). Учитывая, что (здесь учтено, что волна распространяется в вакууме, где e = 1 и m = 1). Тогда искомые амплитуды Em и Hm:
Подставляя числовые данные, получим
2) Давление, оказываемое электромагнитной волной на тело, полностью ее поглощающее, определяется средним значением объемной плотности энергии в падающей волне, т.е. p = < w>.
Согласно определению, мгновенное значение объемной плотности энергии:
а среднее значение
Учитывая связь величин Em и Нm, а также то обстоятельство, что волна распространяется в вакууме, получим
Так как скорость распространения электромагнитных волн в вакууме < w> = < S> /c.
Тогда искомое давление p = < S> /c. Подставив числовые данные, получим p = 1340/(3× 108) = 4, 5× 10-6 Па = 4, 5 мкПа. 6. Монохроматический пучок света с длиной волны l = 0, 6 мкм падает под углом a = 30о на находящуюся в воздухе мыльную пленку (показатель преломления мыльной воды n = 1, 33). При какой наименьшей толщине dmin пленки отраженный свет будет максимально усилен интерференцией? Максимально ослаблен?
Луч света от источника S падает на поверхность пластинки, частично отражаясь и частично преломляясь в точке А. Оптическая разность хода между лучами SABCP(луч 2) и SAEP (луч 1): D = (AB+BC)× n – (AE + l/2), где величина l/2 представляет собой добавочную разность хода, возникающую при отражении световой волны (луч 1) в точке А от оптически более плотной, чем воздух, среды (мыльная вода). При отражении преломленного луча в точке В на границе между водой и воздухом подобная добавочная разность хода не возникает, так как луч отражается от оптически менее плотной среды (воздух). Из рис. 14 АВ = ВС = d/cosb; AE = ACsina = 2dtgbsina.
Воспользовавшись законом преломления sina = nsinb, запишем выражение АЕ в виде АЕ = 2dn× sin2b/cosb. Подставив в выражение оптической разности хода D вместо АВ, ВС и АЕ их значения, найдем Таким образом, D представляет собой ту оптическую разность хода, с которой лучи интерферируют в точке Р. Максимумам интенсивности соответствует условие D = kl или
минимумам интенсивности – условие D = (2k + 1)× l/2 или Таким образом, можно найти набор возможных значений толщины d пленки, при которой свет будет максимально усилен:

d = dmin при k = 0, т.е. Аналогично определим возможные значения толщины d пленки, при которой свет будет максимально ослаблен:
d = dmin при k = 0, т.е. Подставив числовые данные, получим
7. Дифракционная решетка имеет ширину 25 мм и содержит 250 штрихов на 1 мм. Фокусное расстояние объектива, в фокальной плоскости которого находится экран, равно 80 см. Свет падает на решетку нормально. Исследуемый спектр содержит спектральные линии с длинами волн l1 = 310, 54 нм и l2 = 310, 184 нм. Определить: а) общее число дифракционных максимумов, которое дает дифракционная решетка; б) расстояние на экране между данными спектральными линиями в спектрах первого и второго порядков; в) будут ли они разрешены в этих порядках спектра.
Решение Для того чтобы наблюдение дифракционной картины проводить в параллельных лучах, следует расположить экран наблюдения бесконечно далеко от решетки либо за решеткой поместить собирающую линзу с фокусным расстоянием F, а экран наблюдения - в ее фокальной плоскости. В этом случае в каждую точку экрана будут приходить вторичные волны, образующие за решеткой плоский волновой фронт, повернутый по отношению к фронту падающей волны на определенный угол дифракции j. Те углы дифракции, для которых волны, излучаемые всеми щелями, будут усиливать друг друга, соответствуют главным максимумам. Благодаря периодичности решетки, достаточно найти условия, при которых волны, излучаемые двумя соседними щелями, усиливают друг друга. Это происходит тогда, когда оптическая разность хода D между вторичными волнами, излученными соответственными источниками двух соседних щелей, равна целому числу длин волн: D = d× sinj = kl, где k = 0, ±1, ±2,.. а) Для определения общего числа дифракционных максимумов, даваемых данной дифракционной решеткой, вычислим сначала максимальное значение kmax, соответствующее максимуму наибольшего порядка, исходя из того, что максимальный угол отклонения лучей решеткой не может превышать 90°. kmax = d× sin90°/l. Здесь d=1/n. Подставив числовые данные, получим kmax = 12, 8968 для l1 и kmax = 12, 8956 для l2. Число k должно быть целым. В то же время оно не может принять значение, равное 13, так как при этом значении sinj должен быть больше единицы, что невозможно. Следовательно, kmax = 12. Общее число N максимумов дифракционной картины, полученной с помощью данной решетки, определяется следующим образом: N = 2kmax + 1, так как влево и вправо от центрального (нулевого) максимума будет наблюдаться по одинаковому числу максимумов, равному kmax (всего 2 kmax), и плюс нулевой максимум. Таким образом, N = 2× 12 + 1 = 25. б) Найдем положения на экране дифракционных максимумов k-ого порядка для спектральных линий с длинами волн l1 и l2:
l 1 = F× tgj1; l 2 = F× tgj2, где j1 и j2 – углы дифракции спектральных линий l1 и l2 соответственно. Используя формулу дифракционной решетки, получим
Искомое расстояние D l на экране между спектральными линиями l1 и l2 в спектре k-го порядка:
Произведя соответствующие вычисления, получим
D l 1 = 6, 1× 10-6 м при k = 1, D l 2 = 12, 4× 10-6 м при k = 2.
в) Для того чтобы две спектральные линии с длинами волн l1 и l2 были разрешены, т.е. видны раздельно в спектре, необходимо минимальное значение разрешающей способности дифракционной решетки:
Разрешающую способность решетки в спектре k-го порядка можно определить по формуле R = kN, где N – общее число штрихов решетки. Таким образом, R = k× b/d = kbn. Отсюда разрешающая способность данной решетки в спектре 1-го порядка R(1) = 1× 2, 5× 10-2× 2, 5× 105 = 6250, а в спектре 2-го порядка R(2) = 22, 5× 10-2× 2, 5× 105 = 12 500. Следовательно, в спектре 1-го порядка две спектральные линии с длинами волн l1 и l2 разрешены не будут, а в спектре 2-го порядка они разрешены.
8. Естественный свет падает на систему из трех последовательно расположенных одинаковых поляризаторов, причем направление главной плоскости среднего поляризатора составляет угол j = 60о с направлением главных плоскостей двух других поляризаторов. Каждый поляризатор обладает поглощением таким, что при падении на него света коэффициент пропускания составляет 0, 81. Во сколько раз уменьшится интенсивность света после прохождения этой системы?
Решение Рассмотрим процесс прохождения света последовательно через первый, второй и третий поляризаторы. Интенсивность I0 естественного света, прошедшего через первый поляризатор, ослабляется в два раза при условии 100-процентного пропускания света поляризатором. Если коэффициент пропускания t = 0, 81 (или 81 %), то интенсивность I1 поляризованного света, вышедшего из первого поляризатора, будет определяться соотношением I1 = t× I0/2.
Интенсивность I2 света, выходящего из второго поляризатора, определяется законом Малюса I2 = I1cos2j, при условии 100-процентного пропускания света поляризатором. Угол j – это угол между главными плоскостями первого и второго поляризаторов. Учитывая потери интенсивности на поглощение и отражение, интенсивность поляризованного света, вышедшего из второго поляризатора: I2 = t× I1× cos2j = t2× Рассуждая аналогичным образом, получим, что интенсивность поляризованного света, вышедшего из третьего поляризатора, определяется соотношением I3 = t× I2× cos2j = t3× Таким образом, интенсивность света, прошедшего через систему трех поляризаторов, ослабляется в I0/I3 раз. Подставляя числовые данные, получим
Задачи для самостоятельного решения
1. Складываются два колебания одинакового направления, выражаемых уравнениями: x1 = cosp(t + 1/6) см и x2 = 2cosp(t + 1/2) см. Определить амплитуды, периоды и начальные фазы складываемых и результирующего колебаний, написать уравнение результирующего колебания. Ответ: T1 = T2 = 2 c; xm1 = 1 см; j1 = p/6 рад.; xm2 = 2 см; j2 = p/2 рад.; T = 2 с; xm = 2, 64 см; j = 0, 39p рад. Уравнение результирующего колебания: x = 2, 64cos(pt + 0, 4) см.
2. Найти максимальное значение амплитуды смещения осциллятора, совершающего установившиеся колебания под действием вынуждающей гармонической силы с амплитудой F0 = 2, 5 Н, если частота затухающих колебаний данного осциллятора w = 100 с-1 и коэффициент сопротивления среды r = 0, 5 кг/с. Ответ: xmax = F0/(rw) = 0, 05 м.
3. Найти смещение x от положения равновесия точки, отстоящей от источника колебаний на расстояние l = l/12; в момент времени t = T/6. Амплитуда колебаний xm = 0, 05 м. Ответ: x = 2, 5 см.
4. Колебательный контур имеет емкость 1, 1 нФ и индуктивность 5× 10-3 Гн. Логарифмический декремент затухания равен 0, 005. За сколько времени потеряется вследствие затухания 99 % энергии контура? Ответ: t = T× ln100/(2l) = 6, 8 мс.
5. В вакууме вдоль оси x распространяется плоская электромагнитная волна. Интенсивность волны, то есть средняя энергия, проходящая через единицу поверхности за единицу времени составляет 4, 71 мВт/м2. Определить амплитуду напряженности магнитного поля волны. Ответ: Hm = 5 мА/м.
6. На пленку толщиной d = 367 нм падает под углом a параллельный пучок белого света. Показатель преломления пленки n = 1, 4. В какой цвет будет окрашен свет, отраженный пленкой, если a равен: а) 90о; б) 60о? Ответ: а) красный цвет (l = 640 нм); б) синий цвет (l = 538 нм).
7. На каком расстоянии друг от друга будут находиться на экране две спектральные линии с длинами волн l1 = 577 нм и l2 = 579, 1 нм в спектре первого порядка, полученном при помощи дифракционной решетки. Фокусное расстояние линзы, проектирующей спектр на экран, равно 0, 6 м. Период решетки d = 2 мкм. Максимум какого наибольшего порядка дает эта решетка? Какое наименьшее число штрихов должна содержать решетка для разрешения данных спектральных линий в спектре наибольшего порядка? Ответ: 0, 72 мм; 3; 92.
8. Луч естественного света падает на систему из N последовательно расположенных поляризаторов, главная плоскость каждого из которых повернута на угол j = 10° относительно главной плоскости предыдущего поляризатора. В каждом поляризаторе поглощается 5 % падающего на него светового потока. Какая часть естественного света проходит через эту систему? Решить задачу для случая: а) N = 2; б) N = 4; в) N = 8. Ответ: а) 0, 44; б) 0, 37; в) 0, 27.
|


 , (52)
, (52) . (53)
. (53)

 , где j – угол дифракции. Таких зон на ширине щели укладывается
, где j – угол дифракции. Таких зон на ширине щели укладывается  . Если N четное, то в точке Р – минимум, если N нечетное, то в точке P – максимум. Тогда
. Если N четное, то в точке Р – минимум, если N нечетное, то в точке P – максимум. Тогда (54)
(54)
 (57)
(57)

 1. Материальная точка массой m = 5 г совершает гармонические колебания с частотой n = 0, 5 Гц. Амплитуда xm = 3 см. Определить: а) Скорость точки в момент времени, когда координата х = 1, 5 см; б) максимальную силу Fmax, действующую на
1. Материальная точка массой m = 5 г совершает гармонические колебания с частотой n = 0, 5 Гц. Амплитуда xm = 3 см. Определить: а) Скорость точки в момент времени, когда координата х = 1, 5 см; б) максимальную силу Fmax, действующую на 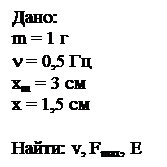 эту точку; в) полную энергию Е колеблющейся точки.
эту точку; в) полную энергию Е колеблющейся точки. х = xmcos(wt + j) (1). Для нахождения проекции скорости точки возьмем первую производную по времени от координаты х
х = xmcos(wt + j) (1). Для нахождения проекции скорости точки возьмем первую производную по времени от координаты х
 2. Гиря массой 0, 5 кг подвешена к пружине, жесткость которой k = 32, 0 Н/м и совершает затухающие колебания. Определить их период, если за время двух колебаний (N = 2) амплитуда уменьшилась в h = 20 раз. Какова добротность данного осциллятора, если под действием вынуждающей вертикальной гармонической силы с частотой W = 10 с-1 гиря будет совершать установившиеся колебания. При этом смещение гири будет отставать по фазе от вынуждающей
2. Гиря массой 0, 5 кг подвешена к пружине, жесткость которой k = 32, 0 Н/м и совершает затухающие колебания. Определить их период, если за время двух колебаний (N = 2) амплитуда уменьшилась в h = 20 раз. Какова добротность данного осциллятора, если под действием вынуждающей вертикальной гармонической силы с частотой W = 10 с-1 гиря будет совершать установившиеся колебания. При этом смещение гири будет отставать по фазе от вынуждающей  силы на j = 3p/4.
силы на j = 3p/4. 2) Под действием вынуждающей силы гиря совершает установившиеся гармонические колебания.
2) Под действием вынуждающей силы гиря совершает установившиеся гармонические колебания.
 ,
,
 . (1)
. (1) . Подставив числовые значения, получим T = 0, 81 c.
. Подставив числовые значения, получим T = 0, 81 c.


 3. Поперечная волна распространяется вдоль упругого шнура со скоростью u = 15 м/с. Период Т колебаний точек шнура равен 1, 2 с, амплитуда xm = 2 м. Определить: а) длину волны l; б) фазу j колебаний, смещение
3. Поперечная волна распространяется вдоль упругого шнура со скоростью u = 15 м/с. Период Т колебаний точек шнура равен 1, 2 с, амплитуда xm = 2 м. Определить: а) длину волны l; б) фазу j колебаний, смещение  , скорость
, скорость  и ускорение
и ускорение  точки, отстоящей на расстоянии х = 45 м от источника волны в момент t = 4 с.; в) разность фаз Dj колебаний двух точек, лежащих на луче и отстоящих от источника волн на расстояниях х1 = 20 м. и х2 = 30 м.
точки, отстоящей на расстоянии х = 45 м от источника волны в момент t = 4 с.; в) разность фаз Dj колебаний двух точек, лежащих на луче и отстоящих от источника волн на расстояниях х1 = 20 м. и х2 = 30 м. Решение
Решение .
. .
. .
. .
.
 Решение
Решение q = qmsin(w0t + j0)
q = qmsin(w0t + j0)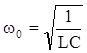 – собственная частота колебательного контура,
– собственная частота колебательного контура, ,
,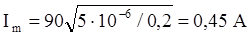 .
. .
. ,
,
 , получим
, получим 


 ,
, .
. .
. , запишем
, запишем
 Решение
Решение Пусть луч света, исходящий из источника S, падает под углом a на плоскопараллельную пленку (пластинку) некоторой толщины d (рис. 14). Интерференционная картина наблюдается в точке P фокальной плоскости собирающей линзы в результате наложения световых лучей, отразившихся от верхней и нижней поверхностей пленки. В зависимости от оптической разности хода D этих лучей в точке Р будет наблюдаться усиление или ослабление колебаний света.
Пусть луч света, исходящий из источника S, падает под углом a на плоскопараллельную пленку (пластинку) некоторой толщины d (рис. 14). Интерференционная картина наблюдается в точке P фокальной плоскости собирающей линзы в результате наложения световых лучей, отразившихся от верхней и нижней поверхностей пленки. В зависимости от оптической разности хода D этих лучей в точке Р будет наблюдаться усиление или ослабление колебаний света.

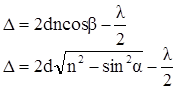

 где k = 0, 1, 2,...
где k = 0, 1, 2,... .
.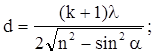
 .
.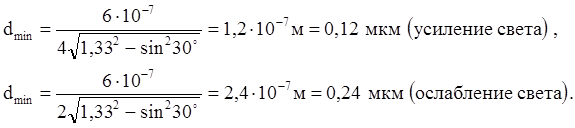
 .
. .
.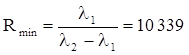 .
. .
. .
.



