Электромагнитные колебания
При электромагнитных колебаниях в колебательной системе происходят периодические изменения физических величин, связанных с изменениями электрического и магнитного полей. Простейшей колебательной системой такого типа является колебательный контур, то есть цепь, содержащая индуктивность и емкость. Благодаря явлению самоиндукции в такой цепи возникают колебания заряда на обкладках конденсатора, силы тока, напряженностей электрического поля конденсатора и магнитного поля катушки, энергии этих полей и т.д. При этом математическое описание колебаний оказывается полностью аналогичным рассмотренному выше описанию механических колебаний. Приведем таблицу физических величин, являющихся взаимными аналогами при сравнении двух типов колебаний.
Таким образом, все математические соотношения, приведенные выше, можно перенести на электромагнитные колебания в контуре, заменив все величины на их аналоги. Например, сравним формулы для периодов собственных колебаний:
Налицо их полная идентичность.
Волны
Волна – это процесс распространения колебаний в пространстве. В зависимости от физической природы процесса волны делятся на механические (упругие, звуковые, ударные, волны на поверхности жидкости и т. д.) и электромагнитные. В зависимости от направления колебаний волны бывают продольные и поперечные. В продольной волне колебания происходят вдоль направления распространения волны, а в поперечной – перпендикулярно этому направлению. Механические волны распространяются в некоторой среде (твердой, жидкой или газообразной). Электромагнитные волны могут распространяться и в пустоте. Несмотря на разную природу волн, их математическое описание практически одинаково, подобно тому, как механические и электромагнитные колебания описываются уравнениями одинакового вида.
Механические волны
Приведем основные понятия и характеристики волн. x – обобщенная координата – любая величина, совершающая колебания при распространении волны (например, смещение точки от положения равновесия). l – длина волны – наименьшее расстояние между точками, колеблющимися с разностью фаз 2p (расстояние, на которое волна распространяется за один период колебаний): l = uT, (29) где u – фазовая скорость волны, T – период колебаний. Волновая поверхность – геометрическое место точек, колеблющихся в одинаковой фазе. Фронт волны – геометрическое место точек, до которых дошли колебания к данному моменту времени (передняя волновая поверхность). В зависимости от формы волновых поверхностей волны бывают плоские, сферические и т. п. Уравнение плоской волны, распространяющейся вдоль оси x, имеет вид
x(х, t) = xmcos(wt – kx), (30) где
Уравнение плоской волны, распространяющейся в произвольном направлении:
где Уравнением сферической волны будет
из чего видно, что амплитуда сферической волны убывает по закону 1/r. Фазовая скорость волны, т.е. скорость, с которой движутся волновые поверхности, зависит от свойств среды, в которой распространяется волна.
фазовая скорость упругой волны в газе, где g – коэффициент Пуассона, m – молярная масса газа, T – температура, R – универсальная газовая постоянная.
фазовая скорость продольной упругой волны в твердом теле, где E – модуль Юнга, r – плотность вещества.
фазовая скорость поперечной упругой волны в твердом теле, где G – модуль сдвига. Волна, распространяясь в пространстве, переносит энергию. Количество энергии, переносимой волной через некоторую поверхность в единицу времени, называется потоком энергии Ф. Для характеристики переноса энергии в разных точках пространства вводится векторная величина, называемая плотностью потока энергии
где w – объемная плотность энергии волны в данной точке. Вектор Среднее по времени значение модуля вектора Умова называется интенсивностью волны I. I = < j >. (37)
Электромагнитные волны
Электромагнитная волна – процесс распространения в пространстве электромагнитного поля. Как говорилось ранее, математическое описание электромагнитных волн аналогично описанию механических волн, таким образом, необходимые уравнения можно получить, заменив в формулах (30) – (33) x на
Волна, описываемая уравнениями (38), показана на рис. 5.
Как видно, векторы Рис. 5 электромагнитной волны равна Величина
а интенсивность электромагнитной волны в соответствии с (37) I = < S > (41) Электромагнитная волна, падая на вещество, оказывает на него давление, которое выражается формулой P = < w> (1+r), (42) где r – коэффициент отражения.
Волновая оптика
Волновая оптика рассматривает круг явлений, связанных с распространением света, которые можно объяснить, представляя свет как электромагнитную волну. Основное понятие волновой оптики – световая волна. Под световой волной понимают электрическую составляющую электромагнитной волны, длина волны которой в вакууме
E = Acos(wt – kx + a0), (43)
где А – принятое обозначение амплитуды светового вектора Е, a0 – начальная фаза (фаза при t = 0, x = 0). В среде с показателем преломления n фазовая скорость световой волны равна u = c/n, а длина волны l = l0/n. (44) Интенсивность световой волны, как следует из (41), определяется средним значением вектора Пойнтинга I = < S >, и можно показать, что I ~ A2, (45) т.е. пропорциональна квадрату амплитуды световой волны.
|

 – величина, обратная емкости конденсатора.
– величина, обратная емкости конденсатора.
 – маятник,
– маятник,
 – контур. (28)
– контур. (28)
 – волновое число.
– волновое число. , (31)
, (31) – волновой вектор, направленный по нормали к волновой поверхности.
– волновой вектор, направленный по нормали к волновой поверхности. , (32)
, (32) – (33)
– (33) – (34)
– (34) – (35)
– (35) . Она равна потоку энергии через единичную площадку, перпендикулярную направлению распространению волны, а по направлению совпадает с направлением фазовой скорости волны.
. Она равна потоку энергии через единичную площадку, перпендикулярную направлению распространению волны, а по направлению совпадает с направлением фазовой скорости волны. , (36)
, (36)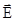 или
или  , где
, где 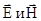 –напряженности электрического и магнитного полей. Например, уравнения плоской электромагнитной волны выглядят следующим образом:
–напряженности электрического и магнитного полей. Например, уравнения плоской электромагнитной волны выглядят следующим образом: . (38)
. (38)
 правовинтовую систему. Колебания этих векторов происходят в одинаковой фазе. В вакууме электромагнитная волна распространяется со скоростью света С = 3× 108 м/с. В веществе фазовая скорость
правовинтовую систему. Колебания этих векторов происходят в одинаковой фазе. В вакууме электромагнитная волна распространяется со скоростью света С = 3× 108 м/с. В веществе фазовая скорость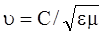 , (39) где e – относительная диэлектрическая проницаемость, m – относительная магнитная проницаемость вещества.
, (39) где e – относительная диэлектрическая проницаемость, m – относительная магнитная проницаемость вещества.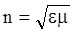 называется при этом абсолютным показателем преломления вещества. Вектор плотности потока энергии электромагнитной волны носит название вектора Пойнтинга
называется при этом абсолютным показателем преломления вещества. Вектор плотности потока энергии электромагнитной волны носит название вектора Пойнтинга  . В соответствии с равенством (36)
. В соответствии с равенством (36) , где w – плотность энергии электромагнитной волны. Кроме того, вектор
, где w – плотность энергии электромагнитной волны. Кроме того, вектор  можно представить в виде:
можно представить в виде:  , (40)
, (40) l0 лежит в пределах 400 – 700 нм. Такие волны воспринимает человеческий глаз. Уравнение плоской световой волны можно представить в виде
l0 лежит в пределах 400 – 700 нм. Такие волны воспринимает человеческий глаз. Уравнение плоской световой волны можно представить в виде


