Плиты покрытий и панели стен
6.1. Плиты покрытий и панели стен предназначаются для применения в качестве ограждающих конструкций в отапливаемых зданиях и сооружениях с относительной влажностью воздуха до 75 % и в неотапливаемых - без выделения водяных паров в районах с расчетной температурой наружного воздуха до - 50° С. 6.2. Плиты покрытий рекомендуются для зданий и сооружений с наружным отводом воды. 6.3. Утепленные плиты состоят из несущего каркаса, наружной и внутренней обшивок, утеплителя и пароизоляции. Неутепленные плиты имеют одну или две обшивки в зависимости от конструкции кровли. 6.4. Каркас плит и панелей выполняется из цельных или клееных пиломатериалов, ребер с фанерной стенкой и гнутоклеенных фанерных профилей. В качестве обшивок используются водостойкая фанера, плоские асбестоцементные листы, древесные плиты (ДВП, ДСП, ЦСП), листовые материалы на основе пластмасс, алюминиевые листы. 6.5. Соединение элементов каркаса с обшивками может осуществляться на водостойких клеях или на податливых связях (шурупы, гвозди, скобы). Фанеру, древесно-волокнистые и древесно-стружечные плиты целесообразно приклеивать к элементам каркаса; асбестоцементные листы, цементно-стружечные плиты, алюминиевые листы и другие следует соединять с каркасом на податливых связях. 6.6. В качестве утеплителя рекомендуются минераловатные плиты на синтетическом связующем, укладываемые на внутреннюю обшивку по слою пленочной или покрасочной пароизоляции. Возможно применение и других эффективных утеплителей, например, заливочных пенопластов. 6.7. Плиты покрытий могут быть использованы под мягкую кровлю из рулонного трехслойного ковра (один слой наклеивается на заводе); жесткую кровлю из волнистых асбестоцементных листов, стальных профилированных настилов и др. Предпочтительнее использовать вариант с жесткой кровлей. 6.8. В плитах покрытий всех типов должна быть обеспечена естественная вентиляция внутренних полостей наружным воздухом. Вентиляция может осуществляться поперек или вдоль ската. В случае устройства кровли из волнистых асбестоцементных листов вентиляция обеспечивается вдоль ската через волны кровельных листов. 6.9. Расчет плит и панелей должен производиться по двум предельным состояниям в соответствии со СНиП II-25-80. В плитах и панелях с обшивками из древесных и листовых материалов нагрузку в основном несет деревянный каркас, а обшивки работают на местный изгиб и продавливание; они несколько повышают жесткость конструкции в целом. При расчете фанерных обшивок на местный изгиб от сосредоточенной силы P = 1, 2 кН рабочая полоса принимается шириной 1 м. Балки 6.10. Для покрытий зданий и сооружений рекомендуются балки клееные и балки из цельной древесины - брусчатые на пластинчатых нагелях. Деревянные клееные балки в зависимости от применяемых материалов подразделяются на: дощатоклееные прямоугольного поперечного сечения, состоящие из склеенных между собой по пласти досок; клеефанерные с поясами из клееной древесины и стенками из водостойкой фанеры. Применение односкатных балок переменного сечения не рекомендуется, а следует использовать балки постоянной высоты, устанавливаемые наклонно вдоль ската.
Рис. 25. Примеры компоновки сечения дощатых клееных балок а) по сортам древесины; б) по породам древесины В практике малоэтажного домостроения нашли применение балки комбинированные, в которых пояса состоят из цельной древесины, а стенки из фанеры или древесноволокнистых плит. Поперечное сечение таких балок может быть двутавровым или коробчатым. Рекомендуемые геометрические параметры балок всех типов даны в табл. 1. 6.11. Дощатоклееные балки подразделяются на прямолинейные и гнутоклееные. Прямолинейные балки могут быть постоянной высоты и двускатные с малым уклоном i ≤ 1: 20 под рулонную кровлю. Высота поперечного сечения гнутоклееных двускатных балок может быть постоянной или переменной. Дощатоклееные балки рекомендуются для пролетов до 18 м. Высота балок назначается не менее 1/15 пролета. Стыкование досок по длине и ширине в слои и склеивание их по высоте выполняются с учетом СНиП II-25-80, пп. 5.5 и 5.7. Варианты компоновки поперечного сечения дощатоклееных балок представлены на рис. 25. 6.12. Расчет дощатоклееных балок на прочность по нормальным напряжениям следует производить по СНиП II-25-80, п. 4.9. В двускатных балках при симметричном загружении тремя и более сосредоточенными грузами или равномерно распределенной нагрузкой расчетное сечение находится от опоры на расстоянии x = lh 0/(2 h), где l - пролет балки; h 0 - высота балки на опоре; принимается не менее половины высоты балки в середине пролета; h - высота балки в середине пролета. Высота расчетного сечения определяется по формуле hx = h 0 + ix, (42) где i - уклон верхнего пояса балки.
Таблица 22
6.13. При действии на балки комбинированной нагрузки, равномерно распределенной и сосредоточенной, положение расчетного сечения определяется по формуле x 0 = K 0 l, (43) где K 0 - коэффициент, принимаемый по табл. 22. В табл. 22 mi, γ и A определяются по формулам mi = Pi /(ql); (0 ≤ i ≤ 4); γ = 2 (h / h 0 - 1); A = 0, 5 + m 2 - α (m 1 + m 2- m 3 - m 4) - α к(m 2 - m 3). Если вычисленный по формулам табл. 22 коэффициент K 0 оказывается меньше левой границы указанного в скобках интервала его допустимых значений, то он принимается равным этому граничному значению; если больше правой границы, то вычисляется снова по следующей из приведенных формул. При действии равномерно распределенной и крановой нагрузок самым невыгодным положением груза является: для двухопорных подвесных кранов - положение под крайней подвеской; для трехопорных и двух двухопорных подвесных кранов в пролете - положение под центральными подвесками; для монорельса с тельфером при одной сосредоточенной силе в пролете (см. табл. 22): по схеме а - u = (h 0/ h) l, по схеме б - u = 0. 6.14. Расчет деревянных балок как изгибаемых элементов должен производиться согласно указаниям СНиП II-25-80 по первой и второй группам предельных состояний. 6.15. Для балок с относительной высотой h / l ≥ 1/10 необходима проверка прочности по главным растягивающим напряжениям σ рα . Проверка производится на нейтральном слое на расстоянии от оси опорной площадки x = 0, 9 h 0 для балок постоянной высоты и x = 1, 1 h 0 для балок переменной высоты. В случае уточненного расчета на ЭВМ при разработке типовых проектов дощатоклееных балок эту проверку следует производить в зоне с координатами x = 0, 8 h 0¸ 1, 2 h 0; Y = ±0, 1 h 0 для балок постоянного сечения; x = h 0¸ 1, 4 h 0; Y = 0 ¸ 0, 15 h 0 для двускатных балок переменного сечения; координата берется выше нейтральной оси. Проверка выполняется по формуле σ рα = 0, 5[σ x + σ y + где σ x - нормальные напряжения вдоль волокон; σ y = σ q + σ р - суммарные нормальные напряжения поперек волокон; σ q = q /(2 b) - напряжения поперек волокон от равномерно распределенной нагрузки q на уровне нейтральной оси; σ р = -4 P cos4 (arctg (2 x / hx))/(π bhx) - напряжения поперек волокон от опорного давления и сосредоточенных сил на уровне нейтральной оси; τ xy - скалывающие напряжения на уровне нейтральной оси в балках с постоянной высотой определяются по СНиП II-25-80, п. 4.10, а в балках с переменной высотой - по формуле τ xy = 3(Qx - iMx / hx)/(2 bhx),
Рис. 26. График зависимости расчетных сопротивлений растяжению (МПа) клееной древесины сосны и ели от угла наклона к волокнам для 1, 2 и 3 сортов
Рис. 27. Гнутоклееные балки а) постоянной высоты; б)переменной высоты где i - уклон верхней грани балки; α - угол, определяющий направление главных растягивающих напряжений; вычисляется по формулам: при σ x - σ y ≥ 0 α = 0, 5arctg [2τ xy /(σ x - σ y)]; при σ x - σ y < 0 α = 0, 5{180° + arctg [2τ xy /(σ x - σ y)]}; R рα - расчетное сопротивление древесины растяжению под углом к волокнам α; принимается по графику рис. 26; x - расстояние от оси опорной площадки до проверяемой точки по горизонтали; y - расстояние от нейтральной оси сечения до проверяемой точки по вертикали; положительные значения принимает ниже нейтральной оси; b - ширина балки; h 0, hx - высота балки на опоре и в сечении x; Qx, Mx, Jx - поперечная сила, изгибающий момент и момент инерции балки в сечении x. 6.16. Двускатные гнутоклееные балки с постоянной и переменной высотой поперечного сечения и криволинейным участком в средней части пролета (рис. 27) рекомендуются при уклонах 10 - 25 %. Одна из опор в таких балках независимо от пролета должна быть подвижной во избежание возникновения распора. Расчет гнутоклееных балок переменной высоты производится в приведенном ниже порядке. Определяются максимальный изгибающий момент и опорные реакции. Предварительно задается ширина сечения b и назначается длина криволинейного участка l 1= (0, 1 - 0, 3) l. Назначается уклон нижней грани i 2, равный или несколько меньший уклона верхней грани i 1 (на величину не более 7 - 10 %). Вычисляются углы наклона граней балки γ и φ и радиус кривизны нижней грани r 0. В случае, если уклоны граней заданы в %, γ = arctg 0, 01 i 1, r 0 = l 1(2sin φ). φ = arctg 0, 01 i 2. Выбирается толщина досок для гнутоклееных конструкций и назначается коэффициент m гн в соответствии с СНиП II-25-80, п. 3.2, ж. Рекомендуется принимать отношение r к/ a ≥ 500, тогда коэффициент m гн = 1 для всех видов сопротивлений. Определяется предварительно высота балки в середине пролета из условия восприятия изгибающего момента (см. рис. 27) h = принимая в первом приближении b ≥ 12 см, m б ≈ 0, 85 и K и = 1, 3, где K и - коэффициент, учитывающий кривизну криволинейного участка и уклон верхней грани. При заданном уклоне кровли вычисляется значение высоты балки на опоре h 0 = h 1 - 0, 5 l (tgγ - tgφ), где h 1 = h - 0, 5 l 1tg φ + r 0(1 - cos φ). Положение расчетного сечения для проверки нормальных напряжений изгиба определяется по формуле x = lh 0/(2 h 1). Если определенное по этой формуле расчетное сечение находится в пределах прямолинейной зоны балки, то далее в этом сечении производится проверка нормальных напряжений изгиба как в прямолинейных двускатных балках. Если же расчетное сечение находится в пределах криволинейной зоны, то расчет следует производить с учетом уточнения высоты балки в этом сечении из-за искривленности нижней грани hx = h - r 0[cos (γ - φ x)/cos γ - 1], где φ x = arcsin [(0, 5 l - x)/cos γ ]. 6.17. Проверка максимальных радиальных растягивающих напряжений, действующих поперек волокон древесины, и краевых тангенциальных нормальных напряжений изгиба вдоль волокон древесины производится по формулам: σ r = KrM макс/ W макс ≤ R р90, σ и = K и M макс/ W макс ≤ R и, где M макс и W макс - изгибающий момент и момент сопротивления в середине пролета; Kr и K и - коэффициенты, учитывающие кривизну криволинейного участка и угол наклона верхней грани γ; определяются по графикам на рис. 28, 29 в зависимости от безразмерных параметров h / r, h / l и γ, где r = r 0 + 0, 5 h - радиус кривизны геометрической оси балки в середине пролета. Если вычисленные максимальные радиальные напряжения выше допустимых расчетных величин, то следует либо увеличить радиус кривизны, или уменьшить, если возможно, уклон верхней грани балки и далее осуществить повторную проверку радиальных напряжений, либо следует запроектировать усиление конькового узла вклеенными штырями. 6.18. Проверка максимальных скалывающих напряжений производится по СНиП II-25-80, формула (18).
Рис. 28. График для определения коэффициента Kпри расчете гнутоклееных балок переменной высоты ---------чистый изгиб; - - - - - равномерно распределенная нагрузка; 1 - h / r = 1/16; 2 - h / r = 1/13; 3 - h / r = 1/10
Рис. 29. График для определения коэффициента Kипри расчете гнутоклееных балок переменной высоты 6.19. Прогиб определяется согласно СНиП II-25-80, п. 4.33, а горизонтальное перемещение по формуле Δ l = f (tgγ + tg φ) ≤ 4 см. 6.20. В гнутоклеенных балках постоянной высоты при действии нагрузки на всем пролете для напряжений изгиба вдоль волокон древесины и радиальных растягивающих напряжений поперек волокон древесины расчетным является сечение в середине пролета. Проверка напряжений изгиба осуществляется по формуле σ и = (M / W) K и ≤ R и, где K и = 1 + 0, 5 h / r. Проверка максимальных радиальных напряжений, зависящих от кривизны криволинейного участка и параметра h / l, осуществляется по формуле σ r = (M / W) Kr ≤ R р90, где Kr = 0, 25 h / r - 0, 083(h / l - 0, 034). В случае чистого изгиба коэффициент Kr = 0, 25 h / r. 6.21. Клеефанерные балки с плоскими стенками рекомендуются для пролетов до 18 м (см. табл. 1). В ряде случаев возможно применение таких балок с верхним и нижним наклонными поясами. Уклон верхнего пояса рекомендуется не более 25 %, нижнего - на 5 - 10 % меньше. В балках пролетом более 12 м предпочтение следует отдавать двухстенчатым двутавровым поперечным сечениям. В случае необходимости возможно введение в приопорных зонах дополнительных стенок. Пояса клеефанерных балок выполняются из вертикальных слоев пиломатериалов толщиной не более 33 мм. Из горизонтальных слоев выполняются только криволинейные участки поясов (СНиП II-25-80, п. 6.20). При конструировании клеефанерных балок направление наружных слоев фанеры рекомендуется ориентировать параллельно их нижнему поясу. Листы фанеры между собой и с древесиной соединяются в соответствии с указаниями СНиП II-25-80, пп. 5.6 – 5.8. Для обеспечения местной устойчивости стенок по длине балок устанавливаются ребра жесткости, которые рекомендуются совмещать со стыками фанеры «на ус». У опор в случае необходимости ребра устанавливаются чаще. 6.22. Расчет клеефанерных балок производится по методу приведенного сечения по указаниям СНиП II-25-80 в части особенностей расчета клееных элементов из фанеры с древесиной. При этом значение модуля упругости фанеры вдоль волокон наружных слоев по СНиП II-25-80, табл. 11, следует повышать на 20 %. Расстояние до расчетного сечения в двускатных балках от оси опоры при симметричном загружении (равномерно распределенной или тремя и более сосредоточенными нагрузками) находится по формуле x = h' 0- высота балки на опоре между осями поясов; l - пролет балки; i - уклон верхнего пояса балки. Высота балки в расчетном сечении hx определяется по формуле (42). 6.23. Проверку прочности по нормальным краевым, максимальным скалывающим и главным растягивающим напряжениям следует производить в соответствии с указаниями СНиП II-25-80, пп. 4.28 – 4.30. При этом R фрα умножается на коэффициент m ф = 0, 8, учитывающий снижение расчетного сопротивления фанеры, стыкованной «на ус», при работе ее на изгиб в плоскости листа. Проверка по главным растягивающим напряжениям в балках осуществляется: при любых нагрузках в зоне первого от опоры стыка фанерных стенок; при сосредоточенных нагрузках - под ближайшей к опоре силой. В консольных балках аналогичная проверка производится под внутренней кромкой растянутого пояса опорного сечения. 6.24. Составные элементы из брусьев или окантованных бревен, сплоченных на пластинчатых нагелях, могут использоваться в качестве балок или сжато-изгибаемых элементов сквозных конструкций пролетами 6 - 21 м с соблюдением соответствующих требований СНиП II-25-80. Дополнительно должны учитываться указания пп. 5.18 – 5.21 и выполняться следующие условия: такие элементы допускается применять при однопролетной схеме работы; в балках пластинки ставятся на участках длиной 0, 4 l от опор и размещаются равномерно. Количество пластинок n пл определяется по формулам: в изгибаемых элементах n пл ≥ 1, 2 M д S бр(I бр T), (45) во внецентренно-сжатых или сжато-изгибаемых элементах n пл ≥ 1, 2 M д S бр/(I бр T) + KN / T, (46) где M д - изгибающий момент, определяемый по деформированной схеме согласно формуле (29) СНиП II-25-80 без учета разгружающего момента от внецентренно приложенной сжимающей силы N, равной N × e; T - расчетная несущая способность пластинки; S бр, I бр - статический момент и момент инерции брутто; K - коэффициент, учитывающий добавочное нагружение пластинок силой N. При передаче силы N: по концам элементов всем брусьям сечения K = 0; двум из трех брусьев (крайнему и среднему) K = 0, 2; одному среднему брусу K = 0, 2; одному крайнему брусу K = 0, 4. Передача части силы N отдельному брусу должна обеспечиваться упором не менее чем на 1/3 его высоты. Заготовка пластинок и выборка гнезд для них в сплачиваемых брусьях должны осуществляться только механизировано с использованием рейсмуса и цепнодолбежника. Составные брусчатые элементы на пластинчатых нагелях должны иметь стрелу выгиба свыше 1/200пролета и быть стянуты у концов и через каждую третью часть пролета 4 болтами диаметром свыше 16 мм. 6.25. При расчете изгибаемых элементов составного сечения на податливых соединениях согласно СНиП II-25-80, пп. 4.9. и 4.33 вводятся соответственно снижающие коэффициенты KW к моменту сопротивления и K ж - к моменту инерции по табл. 13 указанных норм. Для шарнирно опертых по концам составных балок из двух и трех брусьев на металлических пластинах всех типов, вдавливаемых в древесину, коэффициенты KW и K ж рекомендуется определять по формулам: KW = 1/[1 + (n - 1)δ /δ п], K ж = 1/[1 + (n 2 - 1)δ /δ п], где n - число брусьев в составной балке; δ - сдвиговая деформация связей соединения, мм, при полном использовании их несущей способности по табл. 21; δ п - предельное перемещение одного бруса вдоль шва сплачивания от поворота сечения на опоре при отсутствии связей под действием изгибающего момента M б = M / n; здесь M - расчетный изгибающий момент для балки; δ п = nl /(300 K θ ); l - пролет балки, мм; K θ - коэффициент, зависящий от схемы загружения балки; при действии сосредоточенной силы в середине пролета K θ = 4; при равномерно распределенной нагрузке на всем пролете K θ = 3, при действии концевых изгибающих моментов K θ = 2. Пример 1. Запроектировать двускатную дощатоклееную балку прямоугольного сечения пролетом 11, 75 м, покрытие из утепленных плит шириной 1, 5 м, кровля рулонная с уклоном 1: 20 (рис. 30). Балка предназначена в качестве несущей конструкции покрытия сельскохозяйственного производственного здания. Нагрузки: расчетная q = 17 кН/м; нормативная q н = 13 кН/м. Материалы: сухие сосновые строганые доски толщиной 33 мм 2-го и 3-го сорта. Доски 2-го сорта используются в крайних зонах на 0, 15 высоты поперечного сечения (СНиП II-25-80, п. 6.19).
Рис. 30. Двускатная дощатоклеенная балка покрытия Условия эксплуатации: внутри отапливаемых помещений при температуре до 35 °С, с относительной влажностью воздуха от 60 до 75 %. При этих условиях m в = 1 (СНиП II-25-80, табл. 5). Принимаем ширину поперечного сечения b = 14 см, высоту в середине пролета h = 102, 3 см, т.е. l /11, 5 > l /15, тогда высота на опоре h 0 = 72, 6 см. Проверяем максимальные нормальные напряжения по СНиП II-25-80 формула (17) в расчетном сечении x = lh 0/(2 h с) = 1175× 72, 6/(2× 102, 3) = 417 см; высота в этом сечении h 1 = h 0 + ix = 72, 6 + 417× 0, 05 = 93, 5 см; расчетный изгибающий момент Mx = q (l - x) x /2 = 17(11, 75 - 4, 17)4, 17/2 = 268, 7 кН× м. Расчетные сопротивления изгибу и сжатию назначаем для древесины 2-го сорта согласно СНиП II-25-80, пп. 3.1 и 3.2, с введением коэффициентов условий работы m в, m б, m сли коэффициента надежности по назначению γ n согласно СТ СЭВ 384-76. Тогда R и = R с = 15 m в m б m сл/γ n = 15× 1× 0, 86× 1/0, 95 = 13, 6 МПа. Напряжения в расчетном сечении σ x = Mx / Wx = 268, 7× 106/20, 4× 106 = 13, 2 < 13, 6 МПа, где Wx = bh 2 x /6 = 140× 9352/6 = 20, 4× 106 мм3 - момент сопротивления поперечного сечения в расчетном сечении. Проверку прочности по скалыванию производим в опорном сечении [СНиП II-25-80 по формуле (18)]. Поперечная сила на опоре Q = ql /2 = 17× 11, 75/2 = 99, 9 кН; расчетное сопротивление скалыванию вдоль волокон для древесины 2-го сорта R ск = 1, 5 m в m сл/γ n = 1, 5× 1× 1/0, 95 = 1, 58 МПа; скалывающие напряжения QS бр/(I бр b расч) = 99, 9× 103× 3/(2× 726× 140) = 1, 48 < 1, 58 МПа. Проверяем опорную площадку на смятие σ см = Q /(cb) = 99, 9× 103/(250× 140) = 2, 85 < R см.90/γ n = 3/0, 95 = 3, 2 МПа. Поскольку закрепление сжатой кромки осуществляемся ребрами плит через 2× 1, 5 м и, следовательно, l р = 300 < 140 b 2/(hm б) = 140× 142/(102, 3× 0, 85) = 315 (см. п. 4.25), проверка устойчивости плоской формы деформирования не требуется. Прогиб в середине пролета балки находим согласно СНиП II-25-80, пп. 4.32 – 4.33. Предварительно вычисляем к = 0, 15 + 0, 85 h 0/ h = 0, 15 + 0, 85× 72, 6/102, 3 = 0, 753; c = 15, 4 + 3, 8 h 0/ h = 15, 4 + 3, 8× 72, 6/102, 3 = 18, 1; f о = 5× q н l 4/(384 El) = 5× 13× 11, 754× 12× 1012/(384× 10× 140× 1, 0233× 1012) = 25, 7 мм; тогда f = (f / к)[1 + с (h / l)2] = (25, 7/0, 753)[1 + 18, 1(1, 023× 103/11, 75× 103)2 = 38, 8 мм или относительный прогиб f / l = 1/302 < 1/300, т.е. необходимая жесткость балки обеспечена. Пример 2. Определить расчетное сечение в двускатной балке, представленной на рис. 31. Балка нагружена равномерно распределенной нагрузкой q = 14, 8 кН/м, включая собственный вес q св = 1, 3 кН/м, и двумя однопролетными подвесными электрическими кранами грузоподъемностью 10 кН. Положение расчетного сечения определяем по п. 6.13. Вычислим безразмерные величины d = u / l = 150/1800 = 0, 083; α к = u к/ l = 600/1800 = 0, 33; γ = 2(h / h 0 - 1) = 2(159, 8/115, 6 - 1) = 0, 765; m 1 = m 4 = P 1/(ql) = P 4/(ql) = 7, 4/(14, 8× 18) = 0, 028; m 2 = m 3= P 2/(ql) = 27, 4/(14, 8× 18) = 0, 103; A = 0, 5 + m 2 - α (m 1 + m 2 - m 3 - m 4) - α к(m 2 - m 3) = 0, 5 + m 2 = 0, 5 + 0, 103 = 0, 603.
Рис. 31. Расчетная схема дощатоклеенной балки покрытия с подвесным оборудованием Вычислим вначале K 0, предполагая, что расчетное сечение находится на участке между торцом балки и силой P 1 (0 ≤ K 0 ≤ α); K 0= (A + m 1)/[1 + γ (A + m 1)] = (0, 603 + 0, 028)/[1 + 0, 765(0, 603 + 0, 028)] = 0, 426 > α = 0, 083. Это означает, что опасное сечение на рассматриваемом участке не находится. Вычислим K 0, предполагая, что опасное сечение находится на участке между силами P 1 и P 2 (α ≤ K 0 ≤ α + α к) (A - 2γ α m 1)/(1 + γ × A) = (0, 603 - 2× 0, 765× 0, 083× 0, 028)/(1 + 0, 765× 0, 603) = 0, 41 < α + α к =0, 413.
Рис. 32. Двускатная клеефанерная балка покрытия Таким образом, расчетное сечение располагается от торца балки на расстоянии x 0 = K 0 l = 0, 41× 1800 = 738 см. Пример 3. Запроектировать двускатную клеефанерную балку пролетом 18 м переменной высоты с уклоном 1: 15 (рис. 32). Нагрузки: расчетная q = 7кН/м, нормативная q н = 5, 5 кН/м. Материалы: для поясов - сосновые доски сечением 144 ´ 33 мм (после калибровки и фрезерования пиломатериала с сечением 150 ´ 40 мм) с пропилами. В растянутых поясах используется древесина 2-го сорта, в сжатых - 3-го сорта. Для стенок используется фанера клееная, березовая, марки ФСФ В/ВВ толщиной 12 мм. Доски поясов стыкуются по длине на зубчатый шип, фанерные стенки - «на ус». Высоту поперечного сечения балки в середине пролета принимаем h = l /12 = 18/12 = 1, 5 м. Высоту опорного сечения, h 0 = h - 0, 5 li = 1, 5 - 0, 5× 18× 0, 0667 = 0, 9 м. Ширина балки b = Σ δ д + Σ δ ф = 4× 3, 3 + 2× 1, 2 = 15, 6 см. По длине балки укладывается 13 листов фанеры с расстоянием между осями стыков l ф - 10δ ф = 152 - 1, 2× 10 = 140 см. Расстояние между центрами поясов в опорном сечении. h' 0 = h 0 - h н = 0, 9 - 0, 144 = 0, 756 м; 0, 5 h' 0 = 0, 378 м. Расчетное сечение располагается на расстоянии x от оси опорной площадки x = Вычисляем параметры расчетного сечения: высота балки hx = h 0 + ix = 0, 9 + 0, 0667× 6, 9 = 1, 36 м; расстояние между центрами поясов h'x = 1, 36 - 0, 144 = 1, 216 м; 0, 5 h'x = 0, 608 м; высота стенки в свету между поясами hx ст = 1, 216 - 0, 144 = 1, 072 м; 0, 5 hx ст = 0, 536 м. Изгибающий момент в расчетном сечении Mx = qx (l - x)/2= 7× 6, 9(18 - 6, 9)/2 = 268, 1 кН× м; требуемый момент сопротивления (приведенный к древесине) W пр = Mx γ n / R р= 268, 1× 106× 0, 95/9 = 28, 2× 106 мм3; соответствующий ему момент инерции I пр= W пр hx /2 = 28, 2× 106× 1360/2 = 192× 108 мм4. Задаемся двутавровой коробчатой формой поперечного сечения (см. рис. 32). Фактические момент инерции и момент сопротивления сечения, приведенные к древесине, равны I пр = I д + I ф E ф K ф/ E д = 2[(132× 1443/12) + 132× 144× 6082] + 2× 12× 13603× 0, 9× 1, 2/12 = 195, 5× 108> 192× 108 мм4; W пр = I пр× 2/ hx = 2× 195, 5× 108/1360 = 28, 75× 106> 28, 2× 106 мм3, Здесь K ф = 1, 2 - коэффициент, учитывающий повышение модуля упругости фанеры при изгибе в плоскости листа. Проверяем растягивающие напряжения в фанерной стенке σ фр = MxE ф K ф(W пр E д) = 268, 1× 106× 0, 9× 1, 2(28, 75× 106) = 10, 1 < R фр m ф/γ n = 14× 0, 8/0, 95 = 11, 8 МПа. Здесь m ф = 0, 8 - коэффициент, учитывающий снижение расчетного сопротивления фанеры, стыкованной «на ус», при работе ее на изгиб в плоскости листа. Принимая раскрепление сжатого пояса прогонами или ребрами плит через 1, 5 м, определяем его гибкость из плоскости балки λ y = l р(0, 29 b) = 150(0, 29× 15, 6) = 33, 2 < 70 и, следовательно, φ y = 1 - a (λ /100)2 = 1 - 0, 8(3, 32/100)2 = 0, 91, а напряжения сжатия в поясе σ с= Mx / W пр= 268, 1× 106× 28, 75× 106 = 9, 32 < φ yR с/γ n = 0, 91× 11× 0, 95 = 10, 5 МПа. Проверку фанерных стенок по главным напряжениям производим в зоне первого от опоры стыка на расстоянии x 1 = 1, 385 м (см. рис. 32). Для данного сечения M = qx 1(l - x 1)/2 = 7× 1, 385(18 - 1, 385)/2 = 80, 5 кН× м; Q = q (l /2 - x 1) = 7(18/2 - 1, 385) = 53, 3 кН; h = 0, 9 + 1, 385× 0, 0667 = 0, 99 м; h ст = 0, 99 - 2× 0, 144 ≈ 0, 7 м - высота стенки по внутренним кромкам поясов, откуда 0, 5 h ст = 0, 35 м. Момент инерции данного сечения и статический момент на уровне внутренней кромки, приведенные к фанере: I пр = 83× 108 мм4; S пр = 8, 9× 106 мм3. Нормальные и касательные напряжения, в фанерной стенке на уровне внутренней кромки растянутого пояса σ ст = M × 0, 5 h ст/ I пр = 80, 5× 106× 350/83× 108 = 3, 4 МПа; τ ст = QS пр/(I прΣ δ ф) = 53, 3× 103× 8, 9× 106/(83× 108× 2× 12) = 2, 4 МПа. Главные растягивающие напряжения по СНиП II-25-80 формула (45) 0, 5σ ст + α = 0, 5arctg (2τ ст/σ ст) = 0, 5arctg (2× 2, 4/3, 3) = 27, 5° по графику на рис. 17 (СНиП II-25-80, прил. 5). Для проверки устойчивости фанерной стенки в опорной панели балки вычисляем необходимые геометрические характеристики: длина опорной панели a = 1, 3м (расстояние между ребрами в свету); расстояние расчетного сечения от оси опоры x 2= 0, 7 м; высота фанерной стенки в расчетном сечении h ст = (0, 9 + 0, 7× 0, 0667) - 2× 0, 144 ≈ 0, 66 м h ст/δ ф = 660/12 = 55 > 50; γ = a / h ст = 1, 3/0, 66 ≈ 2. По графикам на рис. 18и 19 прил. 5 для фанеры ФСФ и γ = 2 находим K и = 15 и K τ = 2, 5. Момент инерции и статический момент для расчетного сечения x 2, приведенные к фанере I пр = 74× 108 мм4; S пр = 8, 4× 106 мм3. Изгибающий момент и поперечная сила в этом сечении M = qx 2(l - x 2)/2 = 7× 0, 7(18 - 0, 7)/2 = 42, 4 кН× м; Q = q (l /2 - x) = 7(18/2 - 0, 7) = 58, 1 кН. Нормальные и касательные напряжения в фанерной стенке на уровне внутренней кромки поясов σ ст = M 0, 5 h ст/ I пр = 42, 4× 106× 0, 5× 660/74× 108 = 1, 9 МПа; τ ст = QS пр/(I прΣ δ ф) = 58× 103× 8, 4× 106/(74× 108× 2× 1012) = 2, 75 МПа. По СНиП II-25-80 формула (48) проверяем выполнение условия устойчивости фанерной стенки: а) в опорной панели σ ст/[ K и(100δ / h ст)2] + τ ст/[ K τ (100δ /расч)2] = 1, 9/[15(100/55)2 + 2, 75/[2, 5(100/55)2] = 0, 38 < 1, где h ст/δ = 55; б) в расчетном сечении с максимальными напряжениями изгиба (x = 6, 9 м) при h ст/δ = 1, 21/0, 012 = 101 > 50; γ = a / h ст = 1, 3/1, 22 = 1, 07, K и = 20 и K τ = 3, 5. Напряжения изгиба в фанерной стенке на уровне внутренней кромки поясов σ ст = Mx 0, 5 h ст/ I пр = 268, 1× 106× 536/181× 108 = 7, 9 МПа, где I пр = 181× 108 мм4; τ ст = QxS пр/(I прΣ δ ф) = 14, 7× 103× 12, 8× 106/(181× 108× 2× 12) = 0, 43 МПа, где Q = q (l /2 - x) = 7(18/2 - 6, 9) = 14, 7 кН, S = 12, 8× 106 мм3. Используя СНиП II-25-80, формула (48), получим 7, 9[20(100/101)2] + 0, 43[3, 5(100/101)2] = 0, 53 < 1. Производим проверку фанерных стенок в опорном сечении на срез в уровне нейтральной оси и на скалывание по вертикальным швам между поясами и стенкой в соответствии со СНиП II-25-80, пп. 4.27 и 4.29. Момент инерции и статический момент для опорного сечения, приведенные к фанере, определяем как и ранее I пр = 65, 5× 108 мм4; S пр = 9, 1× 106 мм3; τ ср = QmaxS пр/(I прΣ δ ф) = 7, 9× 103× 9, 1× 106/(65, 5× 108× 2× 12) = 3, 65 < R фср/γ n = 6/0, 95 = 6, 3 МПа; τ ск = QmaxS пр/(I пр nh и) = 7, 9× 103× 9, 1× 106/(65, 5× 108× 4× 144) = 0, 15 < R фск/γ n = 0, 8/0, 95 = 0, 84 МПа. Прогиб клеефанерной балки в середине пролета определяем согласно п. 4.33 по формуле (50) СНиП II-25-80. Предварительно определяем: f = f 0[1 + c (h / l)2]/ к, где f 0 = 5 q н l 4(384 El) = 5× 5, 5× 1012(384× 248× 1012) = 30 мм. Здесь EI = E д I д + E ф I ф = 104× 175× 108 + 104× 0, 9× 1, 2× 67, 5× 108 = 248× 1012 Н× мм2 (СНиП II-25-80, прил. 4, табл. 3); значения коэффициентов к = 0, 4 + 0, 6β = 0, 4 + 0, 6× 900/1500 = 0, 76 и c = (45, 3 - 6, 9β)γ = (45, 3 - 6, 9× 900/1500)2× 144× 132[2× 12(1500 - 144)] = 48, 1; тогда f = 30[1 + 48, 1(1, 5× 103/18× 103)2]/0, 76 = 53 мм и f / l = 53/18× 103 = 1/340 < 1/300 (СНиП II-25-80, табл. 16).
Рис. 33. Составная брусчатая балка на пластинчатых нагелях Пример 4. Запроектировать балку пролетом 5, 8 м, шагом 3 м составного сечения из брусьев на березовых пластинчатых нагелях односкатного покрытия сельскохозяйственного здания (рис. 33). Покрытие холодное, кровля рубероидная с уклоном i = 0, 1. Район строительства - III (по снеговой нагрузке). Согласно СНиП II-6-74 нормативная снеговая нагрузка на горизонтальную проекцию покрытия III района при угле наклона ската кровли α ≤ 25 ° и c = 1 равна P с = 1 кН/м2. Принимая коэффициент собственного веса балки K св = 12, определяем нормативную нагрузку от балки на горизонтальну
|




 ] ≤ R рα , (44)
] ≤ R рα , (44)

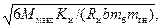


 , где γ = h' 0/(li);
, где γ = h' 0/(li);


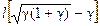 = 18
= 18  = 6, 9 м, где γ = h' 0/(li) = 0, 756(18× 0, 0667) = 0, 63.
= 6, 9 м, где γ = h' 0/(li) = 0, 756(18× 0, 0667) = 0, 63. = 0, 5× 3, 3 +
= 0, 5× 3, 3 +  = 4, 56 < (R рфα /γ n) m ф = (5, 7/0, 95)0, 8 = 4, 8 МПа при угле
= 4, 56 < (R рфα /γ n) m ф = (5, 7/0, 95)0, 8 = 4, 8 МПа при угле



