Упражнения. 4.1.1 Символической записью дать название плоскостей, способ их задания
4.1.1 Символической записью дать название плоскостей, способ их задания. Указать их положение относительно плоскостей П1 и П2. а)
4.1.2 Достроить недостающие проекции прямых t и l, принадлежащих плоскости β (АВС) и θ (θ 2).
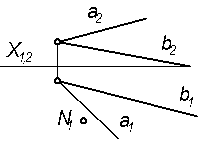
4.1.3 Достроить недостающую проекцию точки N, принадлежащую плоскости α (а∩ b).
Задачи 4.2.1 В плоскости θ (θ 1) построить равнобедренный треугольник АВС с основанием АС= 30 мм. Высота треугольника равна 40 мм.
4.2.2 В плоскости Е (АВС) провести горизонталь через точку D и фронталь через точку Е (взять самостоятельно). Построить недостающие проекции точек D и Е.
4.2.3 Через прямую m провести плоскость: а) горизонтально-проецирующую; б) общего положения.
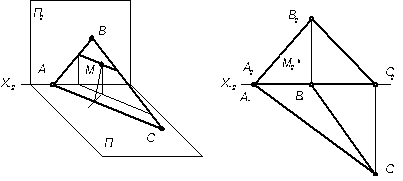
а) б) 4.2.4 Определить длину пути шарика М, катящегося по плоскости S(АВС), и угол наклона этой плоскости к П1. Показать решение этой задачи на пространственном чертеже.
4.2.5 Постройте следы плоскости, заданный двум пересекающимся прямыми АВ и АС. Заданы координаты: А (90; 20; 30), В (70; 10; 60), С (50; 70; 10). 4.2.6 В плоскости Q (АВС) построить произвольный треугольник, стороны которого параллельны плоскостям проекций
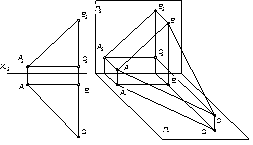
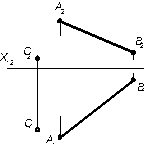
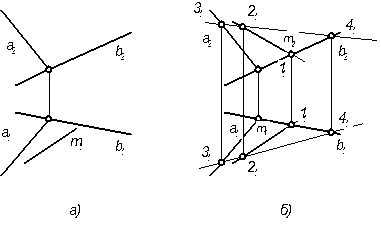
4.2.7 Построить произвольную трехгранную пирамиду, грани которой является плоскостями частного положения, а основание – квадратом. Примеры решения задач: Задача 1 Плоскость задана пересекающимися прямыми: Σ (а∩ b ). Известна горизонтальная проекция прямой m (m1 ), лежащей в этой плоскости. Построить фронтальную проекцию этой прямой линии.
Рисунок3.3 Решение: Прямая m (рис.3.3а), лежащая по условию в плоскости Σ, пересекается прямыми а и b. фронтальные проекции точек пересечения могли бы определить искомую проекцию m 2 Однако точка пересечения прямой m с линией а находится за пределами чертежа, что вынуждает определить вторую точку 2 прямой m с помощью дополнительной прямой линией с (3, 4) плоскости Σ. Задача 2 Определить углы наклона плоскости α (АВС) к плоскостям проекций П1 и П2. Решение: Построим
Рисунок 3.4 Построим
|

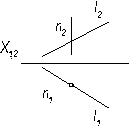 б)
б)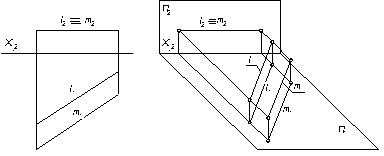 в)
в)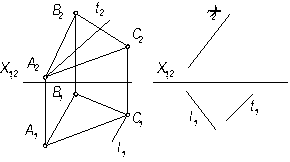

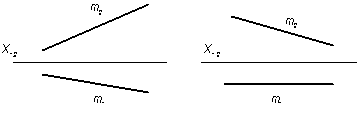
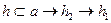 (рис.3.4а). Через точку В1 проведем горизонтальную проекцию (В1 О1 )
(рис.3.4а). Через точку В1 проведем горизонтальную проекцию (В1 О1 )  линии ската (ВО) и построим ее фронтальнуюпроекцию (В2О2). Способом треугольника ∆ О1В1 В* определяем
линии ската (ВО) и построим ее фронтальнуюпроекцию (В2О2). Способом треугольника ∆ О1В1 В* определяем 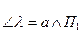
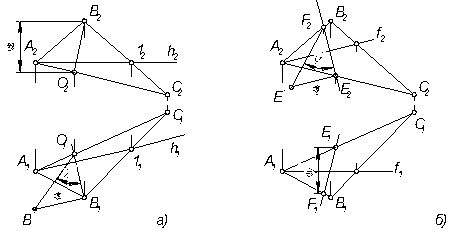
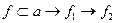 (рис.3.4б) той же плоскости. В произвольном месте построим фронтальную проекцию
(рис.3.4б) той же плоскости. В произвольном месте построим фронтальную проекцию 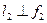 линии наибольшего наклона плоскости а к П2, возьмем на ней отрезок
линии наибольшего наклона плоскости а к П2, возьмем на ней отрезок  и построим горизонтальную проекцию l1 (F1 E1). Способом треугольника через ∆ F2 E2 E* и определяем
и построим горизонтальную проекцию l1 (F1 E1). Способом треугольника через ∆ F2 E2 E* и определяем 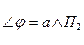 .
.


