Приложение C. 1. Определение эконометрики
Вопросы к экзамену 1. Определение эконометрики. Эконометрический метод и этапы эконометрического исследования. 2. Парная регрессия. Способы задания уравнения парной регрессии. 3. Линейная модель парной регрессии. Смысл и оценка параметров. 4. Оценка существенности уравнения в целом и отдельных его параметров ( 5. Прогноз по линейному уравнению регрессии. Средняя ошибка аппроксимации. 6. Нелинейная регрессия. Классы нелинейных регрессий. 7. Регрессии нелинейные относительно включенных в анализ объясняющих переменных. 8. Регрессии нелинейные по оцениваемым параметрам. 9. Коэффициенты эластичности для разных видов регрессионных моделей. 10. Корреляция и 11. Отбор факторов при построении уравнения множественной регрессии. 12. Оценка параметров уравнения множественной регрессии. 13. Множественная корреляция. 14. Частные коэффициенты корреляции. 15. 16. 17. Фиктивные переменные во множественной регрессии. 18. Предпосылки МНК: гомоскедастичность и гетероскедастичность. 19. Предпосылки МНК: автокорреляция остатков. 20. Обобщенный МНК. 21. Общие понятия о системах эконометрических уравнений. 22. Структурная и приведенная формы модели. 23. Проблема идентификации. Необходимое условие идентифицируемости. 24. Проблема идентификации. Достаточное условие идентифицируемости. 25. Методы оценки параметров структурной формы модели. 26. Основные элементы временного ряда. 27. Автокорреляция уровней временного ряда и выявление его структуры. 28. Моделирование сезонных колебаний: аддитивная модель временного ряда. 29. Моделирование сезонных колебаний: мультипликативная модель временного ряда. 30. Критерий Дарбина-Уотсона.
|

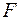 -критерий Фишера и
-критерий Фишера и  -критерий Стьюдента).
-критерий Стьюдента).


