Тепловое излучение является электромагнитным излучением с длиной волны, относящейся к инфракрасной части спектра
 . Энергия, излучаемая поверхностью нагретого тела, является энергией электромагнитных волн. Тепловое излучение вносит существенный вклад в процессы теплообмена уже при температурах в несколько десятков градусов Цельсия. Тепловое излучение нагретых тел является одним из важнейших явлений, используемых при дистанционной диагностике высоковольтного электроэнергетического оборудования. Широкое распространение тепловизоров и пирометров для диагностики токоведущих и изоляцонных элементов электроэнергетического оборудования подтверждает это.
. Энергия, излучаемая поверхностью нагретого тела, является энергией электромагнитных волн. Тепловое излучение вносит существенный вклад в процессы теплообмена уже при температурах в несколько десятков градусов Цельсия. Тепловое излучение нагретых тел является одним из важнейших явлений, используемых при дистанционной диагностике высоковольтного электроэнергетического оборудования. Широкое распространение тепловизоров и пирометров для диагностики токоведущих и изоляцонных элементов электроэнергетического оборудования подтверждает это.
Всякое излучение есть электромагнитные колебания, распространяющиеся в пространстве. Электродинамическая модель излучения совпадает с релятивистским уравнением Шредингера, которое описывает движение квазичастиц — фотонов которые в соответствии с законом Планка обладают энергией  . Уравнение Шредингера для фотонов, движущихся со скоростью света
. Уравнение Шредингера для фотонов, движущихся со скоростью света  м/с, несколько отличается от описанного в разделе 1 и имеет вид
м/с, несколько отличается от описанного в разделе 1 и имеет вид

Исследуем закономерности теплового излучения с помощью модели фотонов, находящихся в полости в термодинамическом равновесии. Фотоны подчиняются статистике Бозе–Эйнштейна и при этом обладают двумя внутренними степенями свободы, поскольку у электромагнитной волны имеет место два типа поляризации.
Бозонная функция распределения (см. раздел 2.3)

была использована М. Планком в работе, где впервые было введено понятие кванта энергии (1900 г.). В согласии с экспериментом он нашел, что

где  — число фотонов, приходящихся на собственные колебания, или моды полости, частота которых равна ω. Здесь
— число фотонов, приходящихся на собственные колебания, или моды полости, частота которых равна ω. Здесь 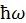 — энергия светового колебания или состояния, занятого единственным фотоном. Термин фотон обозначает квант энергии электромагнитного поля. Распределение Планка в отличие от полученной нами бозонной функции распределения не содержит химического потенциала
— энергия светового колебания или состояния, занятого единственным фотоном. Термин фотон обозначает квант энергии электромагнитного поля. Распределение Планка в отличие от полученной нами бозонной функции распределения не содержит химического потенциала  . Причина такого различия заключается в несохранении числа фотонов, тогда как при выводе функции распределения из основных принципов мы предполагали сохранение полного числа частиц в сумме системы и резервуара. В модели электромагнитное излучение в полости полное число фотонов в системе и резервуаре не сохраняется. Поэтому теперь не следует обращаться к изменению энтропии
. Причина такого различия заключается в несохранении числа фотонов, тогда как при выводе функции распределения из основных принципов мы предполагали сохранение полного числа частиц в сумме системы и резервуара. В модели электромагнитное излучение в полости полное число фотонов в системе и резервуаре не сохраняется. Поэтому теперь не следует обращаться к изменению энтропии  , при помощи которого мы первоначально вводили химический потенциал.
, при помощи которого мы первоначально вводили химический потенциал.
Найдем энергию излучения  , приходящуюся на единичный интервал частоты вблизи некоторого значения
, приходящуюся на единичный интервал частоты вблизи некоторого значения 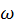

где  — число колебательных мод, приходящихся на единичный интервал частоты. Для того, что бы найти
— число колебательных мод, приходящихся на единичный интервал частоты. Для того, что бы найти  , обратимся к уравнению (85). Рассмотрим его решение в кубе с длиной ребра l. Запишем решение в традиционном для электромагнитных волн виде
, обратимся к уравнению (85). Рассмотрим его решение в кубе с длиной ребра l. Запишем решение в традиционном для электромагнитных волн виде

Поскольку излучение заперто в ящике, то волновая функция ψ обращается в нуль на границах полости  ,
,  ,
,  ,
,  ,
,  ,
,  . Подставим выражение для ψ в уравнение Шредингера (85)
. Подставим выражение для ψ в уравнение Шредингера (85)

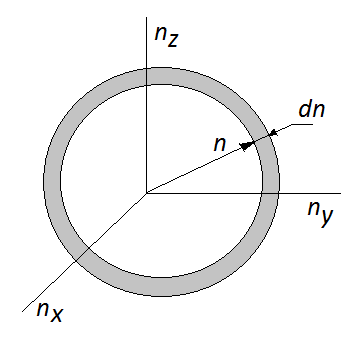 Рис. 46. Пространство квантовых чисел фотонных мод
Рис. 46. Пространство квантовых чисел фотонных мод
|
Отсюда находим связь между частотой и квантовыми числами

где  . Для плотности фотонных мод в пространстве квантовых чисел
. Для плотности фотонных мод в пространстве квантовых чисел  ,
,  ,
,  , применяя для них сферическую систему координат, найдем
, применяя для них сферическую систему координат, найдем

где  — число внутренних степеней свободы фотона, множитель 1/8 присутствует, чтобы выделить положительный октант в пространстве квантовых чисел (рис. 46). Из (86) имеем
— число внутренних степеней свободы фотона, множитель 1/8 присутствует, чтобы выделить положительный октант в пространстве квантовых чисел (рис. 46). Из (86) имеем
 и
и  .
.
Подставляя эти выражения в последнюю формулу для  , получим
, получим

где  — объем полости. Таким образом, для спектральной плотности энергии имеем
— объем полости. Таким образом, для спектральной плотности энергии имеем

Полученное выражение определяет энергию излучения, приходящуюся на единичный интервал частоты. Всю энергию излучения найдем как интеграл

Интеграл в правой части последнего выражения является табличным и равен 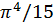 . Поэтому получаем
. Поэтому получаем

Плотность энергии излучения в полости есть

Пусть в одной из стенок кубической полости имеется отверстие единичной площади. Найдем лучистый поток, испускаемый оттуда
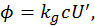
где  — геометрический фактор, учитывающий, что фотоны покидают полость, двигаясь во всех направлениях, а не только по нормали к стенке. После подстановки выражения для
— геометрический фактор, учитывающий, что фотоны покидают полость, двигаясь во всех направлениях, а не только по нормали к стенке. После подстановки выражения для  получим
получим
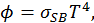
где  — постоянная Стефана–Больцмана.
— постоянная Стефана–Больцмана.
Полученная формула выражает собой закон излучения абсолютно черного тела, т. е. рассмотренного нами случая, когда излучение находится в термодинамическом равновесии с оболочкой (телом), в которой оно заключено, поглощая при этом все излучение, попадающее на его поверхность.
Реальные тела могут отличаться от абсолютно черного тела. При этом лучистый поток с их поверхности сохраняет пропорциональность  , но коэффициент пропорциональности может отличаться от
, но коэффициент пропорциональности может отличаться от  . Поэтому закон излучения Стефана–Больцмана принято записывать в виде
. Поэтому закон излучения Стефана–Больцмана принято записывать в виде
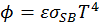 , (87)
, (87)
где  — коэффициент серости или степень черноты тела. Для многих диэлектрических материалов при нормальных условиях степень черноты близка к 1, однако существуют металлы и сплавы, для которой степень черноты измеряется сотыми и даже тысячными долями единицы. Отличие реальных тел от черного тела состоит в том, что для них доля поглощенного излучения меньше 1 и равна
— коэффициент серости или степень черноты тела. Для многих диэлектрических материалов при нормальных условиях степень черноты близка к 1, однако существуют металлы и сплавы, для которой степень черноты измеряется сотыми и даже тысячными долями единицы. Отличие реальных тел от черного тела состоит в том, что для них доля поглощенного излучения меньше 1 и равна 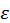 , соответственно доля отраженного излучения составит
, соответственно доля отраженного излучения составит  . Таким образом, мы может трактовать ε, как коэффициент поглощения излучения,
. Таким образом, мы может трактовать ε, как коэффициент поглощения излучения,  — как коэффициент отражения излучения.
— как коэффициент отражения излучения.

 . Энергия, излучаемая поверхностью нагретого тела, является энергией электромагнитных волн. Тепловое излучение вносит существенный вклад в процессы теплообмена уже при температурах в несколько десятков градусов Цельсия. Тепловое излучение нагретых тел является одним из важнейших явлений, используемых при дистанционной диагностике высоковольтного электроэнергетического оборудования. Широкое распространение тепловизоров и пирометров для диагностики токоведущих и изоляцонных элементов электроэнергетического оборудования подтверждает это.
. Энергия, излучаемая поверхностью нагретого тела, является энергией электромагнитных волн. Тепловое излучение вносит существенный вклад в процессы теплообмена уже при температурах в несколько десятков градусов Цельсия. Тепловое излучение нагретых тел является одним из важнейших явлений, используемых при дистанционной диагностике высоковольтного электроэнергетического оборудования. Широкое распространение тепловизоров и пирометров для диагностики токоведущих и изоляцонных элементов электроэнергетического оборудования подтверждает это. . Уравнение Шредингера для фотонов, движущихся со скоростью света
. Уравнение Шредингера для фотонов, движущихся со скоростью света  м/с, несколько отличается от описанного в разделе 1 и имеет вид
м/с, несколько отличается от описанного в разделе 1 и имеет вид


 — число фотонов, приходящихся на собственные колебания, или моды полости, частота которых равна ω. Здесь
— число фотонов, приходящихся на собственные колебания, или моды полости, частота которых равна ω. Здесь 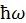 — энергия светового колебания или состояния, занятого единственным фотоном. Термин фотон обозначает квант энергии электромагнитного поля. Распределение Планка в отличие от полученной нами бозонной функции распределения не содержит химического потенциала
— энергия светового колебания или состояния, занятого единственным фотоном. Термин фотон обозначает квант энергии электромагнитного поля. Распределение Планка в отличие от полученной нами бозонной функции распределения не содержит химического потенциала  . Причина такого различия заключается в несохранении числа фотонов, тогда как при выводе функции распределения из основных принципов мы предполагали сохранение полного числа частиц в сумме системы и резервуара. В модели электромагнитное излучение в полости полное число фотонов в системе и резервуаре не сохраняется. Поэтому теперь не следует обращаться к изменению энтропии
. Причина такого различия заключается в несохранении числа фотонов, тогда как при выводе функции распределения из основных принципов мы предполагали сохранение полного числа частиц в сумме системы и резервуара. В модели электромагнитное излучение в полости полное число фотонов в системе и резервуаре не сохраняется. Поэтому теперь не следует обращаться к изменению энтропии  , при помощи которого мы первоначально вводили химический потенциал.
, при помощи которого мы первоначально вводили химический потенциал. , приходящуюся на единичный интервал частоты вблизи некоторого значения
, приходящуюся на единичный интервал частоты вблизи некоторого значения 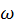

 — число колебательных мод, приходящихся на единичный интервал частоты. Для того, что бы найти
— число колебательных мод, приходящихся на единичный интервал частоты. Для того, что бы найти 
 ,
,  ,
,  ,
,  ,
,  ,
,  . Подставим выражение для ψ в уравнение Шредингера (85)
. Подставим выражение для ψ в уравнение Шредингера (85)
 Рис. 46. Пространство квантовых чисел фотонных мод
Рис. 46. Пространство квантовых чисел фотонных мод

 . Для плотности фотонных мод в пространстве квантовых чисел
. Для плотности фотонных мод в пространстве квантовых чисел  ,
,  ,
,  , применяя для них сферическую систему координат, найдем
, применяя для них сферическую систему координат, найдем
 — число внутренних степеней свободы фотона, множитель 1/8 присутствует, чтобы выделить положительный октант в пространстве квантовых чисел (рис. 46). Из (86) имеем
— число внутренних степеней свободы фотона, множитель 1/8 присутствует, чтобы выделить положительный октант в пространстве квантовых чисел (рис. 46). Из (86) имеем и
и  .
.
 — объем полости. Таким образом, для спектральной плотности энергии имеем
— объем полости. Таким образом, для спектральной плотности энергии имеем

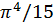 . Поэтому получаем
. Поэтому получаем

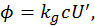
 — геометрический фактор, учитывающий, что фотоны покидают полость, двигаясь во всех направлениях, а не только по нормали к стенке. После подстановки выражения для
— геометрический фактор, учитывающий, что фотоны покидают полость, двигаясь во всех направлениях, а не только по нормали к стенке. После подстановки выражения для  получим
получим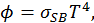
 — постоянная Стефана–Больцмана.
— постоянная Стефана–Больцмана. , но коэффициент пропорциональности может отличаться от
, но коэффициент пропорциональности может отличаться от  . Поэтому закон излучения Стефана–Больцмана принято записывать в виде
. Поэтому закон излучения Стефана–Больцмана принято записывать в виде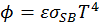 , (87)
, (87) — коэффициент серости или степень черноты тела. Для многих диэлектрических материалов при нормальных условиях степень черноты близка к 1, однако существуют металлы и сплавы, для которой степень черноты измеряется сотыми и даже тысячными долями единицы. Отличие реальных тел от черного тела состоит в том, что для них доля поглощенного излучения меньше 1 и равна
— коэффициент серости или степень черноты тела. Для многих диэлектрических материалов при нормальных условиях степень черноты близка к 1, однако существуют металлы и сплавы, для которой степень черноты измеряется сотыми и даже тысячными долями единицы. Отличие реальных тел от черного тела состоит в том, что для них доля поглощенного излучения меньше 1 и равна 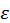 , соответственно доля отраженного излучения составит
, соответственно доля отраженного излучения составит  . Таким образом, мы может трактовать ε, как коэффициент поглощения излучения,
. Таким образом, мы может трактовать ε, как коэффициент поглощения излучения, 


