НЕСТАЦИОНАРНЫЕ ЗАДАЧИ ТЕПЛОПРОВОДНОСТИ
Многие процессы, происходящие в оборудовании больших импульсных токов, в электроэнергетическом оборудовании, протекают сравнительно быстро, их длительность может составлять от нескольких микросекунд до нескольких секунд. В этих условиях температурные поля не успевают устанавливаться, и температура будет зависеть не только от координаты, но и от времени. Для описания таких ситуаций требуется решать нестационарное уравнение теплопроводности (70)
Ниже рассматривается несколько примеров решения нестационарного уравнения теплопроводности. В качестве первого примера рассмотрим процесс проникновения теплового поля в плоское полупространство. Данная модель хорошо описывает ситуацию с нагревом массивного проводника при протекании по нему импульсного тока. Особенность этого процесса состоит в том, что джоулево тепло при протекании короткого (несколько десятков микросекунд и менее) импульса, выделяется в очень тонком поверхностном слое проводника, нагревая поверхность до некоторой начальной температуры (рис. 43). В то же время, в глубине проводника температура остается равной начальной. В дальнейшем в процессе теплопроводности глубокие слои начинают прогреваться. Этот процесс можно описать, используя одномерное нестационарное уравнение теплопроводности

где координата x отсчитывается от поверхности проводника в его глубину (рис. 43). Итак, будем решать одномерное уравнение теплопроводности при начальном условии
где
где
Далее переходим к автомодельной переменной
Подставляя найденные выражения в уравнение для функции f, получим
Для того чтобы исключить из получившегося уравнения время t, выберем значение δ равным
Вводя переменную
которая легко интегрируется
откуда
Интегрирование последнего уравнения дает
Нам остается найти постоянные интегрирования
В разделе 2.4, интеграл, стоящий в левой части последнего выражения, нами был вычислен
При этом
Замечая, что
Полученное решение можно выразить с помощью специальной функции
которая носит название функции ошибок,
На рис. 43 построены рассчитанные по последней формуле распределения температуры в плоской стенке из меди В следующем примере рассчитаем процесс охлаждения предварительно нагретой неограниченной пластины толщиной Применим для решения уже знакомый нам из раздела 1.4 метод разделения переменных. Представим решение в виде произведения функций, каждая из которых зависит только от одной переменной
Подставим данное представление в (80) и разделим получившееся уравнение на
Здесь мы приравняли левую и правую часть получившегося уравнения некоторой константе
Интеграл первого уравнения (74) имеет вид
где
Второе граничное условие
Отсюда видно, что существует бесконечное число констант, удовлетворяющих уравнениям (81)
Соответственно существует бесконечное множество частных решений
Решение второго уравнения (73) есть
Таким образом, частное решение исходного уравнения можно записать как
Общее решение найдем как суперпозицию частных решений
Для того чтобы найти неизвестные постоянные
Умножим полученное равенство на
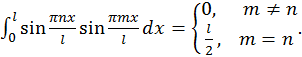
В результате имеем
Отсюда находим постоянные
Решение в окончательном виде
Распределение температуры по толщине медной пластины (
|


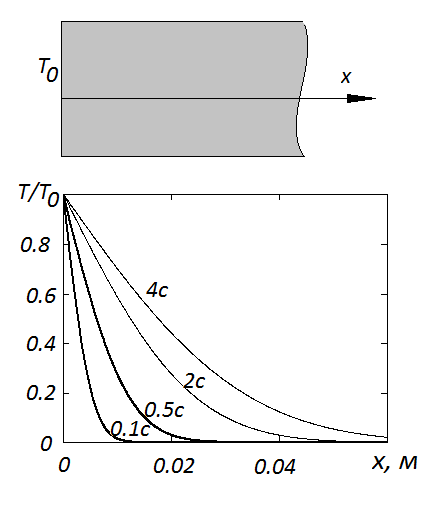 Рис. 43. Распределение температуры в плоской стенке в различные моменты времени
Рис. 43. Распределение температуры в плоской стенке в различные моменты времени
 и при граничных условиях
и при граничных условиях 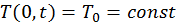 ,
,  . Перепишем последнее уравнение в виде
. Перепишем последнее уравнение в виде
 . Будем искать так называемое автомодельное решение последнего уравнения, для чего представим искомую функцию в виде
. Будем искать так называемое автомодельное решение последнего уравнения, для чего представим искомую функцию в виде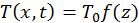 ,
,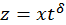 — автомодельная переменная, где параметр δ подлежит определению. После подстановки данного представления решения получим уравнение для функции f:
— автомодельная переменная, где параметр δ подлежит определению. После подстановки данного представления решения получим уравнение для функции f:
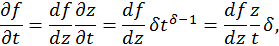
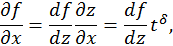

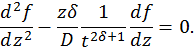
 . В результате придем к обыкновенному дифференциальному уравнению
. В результате придем к обыкновенному дифференциальному уравнению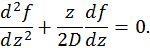
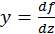 , преобразуем последнее уравнение к форме
, преобразуем последнее уравнение к форме
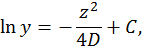
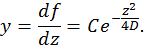

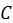 и
и 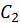 . Вспоминая, что
. Вспоминая, что 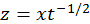 , видим, что
, видим, что  соответствует
соответствует 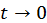 . Поэтому используя начальное условие
. Поэтому используя начальное условие 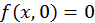 , имеем
, имеем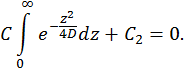

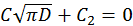 и
и 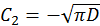 . Выражение для функции
. Выражение для функции 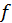 теперь получит вид
теперь получит вид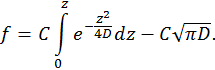
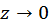 соответствует
соответствует  , используем граничное условие
, используем граничное условие 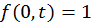 . При этом из последнего выражения для
. При этом из последнего выражения для  . Откуда находим постоянную
. Откуда находим постоянную 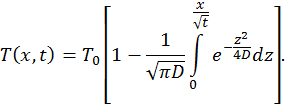

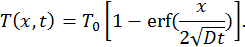
 кг/м3,
кг/м3,  Дж/кг∙ К,
Дж/кг∙ К, 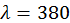 Вт/м∙ К в различные моменты времени. В процессе самостоятельных расчетов нетрудно убедиться, что параметр D определяет скорость проникновения теплового поля в среду. С уменьшением D время диффузии теплового поля возрастает.
Вт/м∙ К в различные моменты времени. В процессе самостоятельных расчетов нетрудно убедиться, что параметр D определяет скорость проникновения теплового поля в среду. С уменьшением D время диффузии теплового поля возрастает.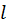 . По-прежнему температура зависит от одной координаты
. По-прежнему температура зависит от одной координаты 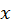 , отсчитываемой по толщине пластины, и времени и описывается одномерным нестационарным уравнением теплопроводности (80). Пластина предварительно нагрета до температуры
, отсчитываемой по толщине пластины, и времени и описывается одномерным нестационарным уравнением теплопроводности (80). Пластина предварительно нагрета до температуры 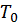 . Поэтому начальным условием будет
. Поэтому начальным условием будет 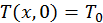 . В момент времени
. В момент времени 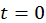 пластина помещается в среду с нулевой температурой, поэтому граничными условиями будет нулевая температура на ее краях
пластина помещается в среду с нулевой температурой, поэтому граничными условиями будет нулевая температура на ее краях 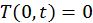 и
и 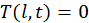 .
.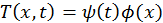 .
.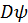 :
: .
.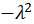 , поскольку равенство должно выполняться всегда при любых изменениях независимых переменных
, поскольку равенство должно выполняться всегда при любых изменениях независимых переменных  , фигурирующих по отдельности в левой и правой части уравнения. Отсюда получаем два уравнения
, фигурирующих по отдельности в левой и правой части уравнения. Отсюда получаем два уравнения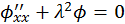 (81)
(81)
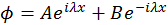 ,
,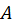 и
и 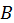 — постоянные. С учетом первого граничного условия
— постоянные. С учетом первого граничного условия 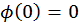 из последнего выражения найдем
из последнего выражения найдем 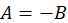 . Тогда
. Тогда .
.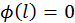 дает
дает  , откуда
, откуда

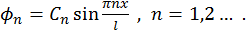
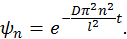
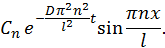

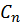 , воспользуемся начальным условием
, воспользуемся начальным условием 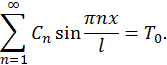
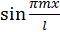 ,
,  и проинтегрируем по x от 0 до l. При этом учтем, что
и проинтегрируем по x от 0 до l. При этом учтем, что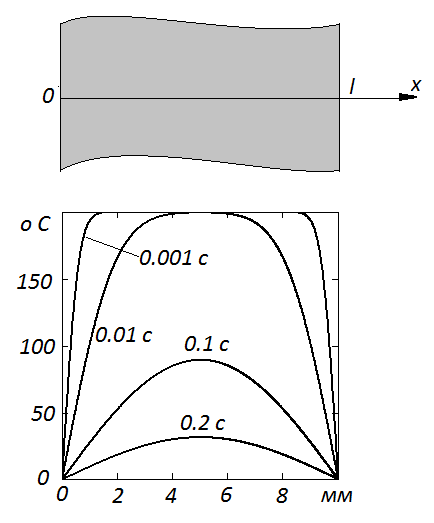 Рис. 44. Распределение температуры в пластине медной пластине в различные моменты времени
Рис. 44. Распределение температуры в пластине медной пластине в различные моменты времени
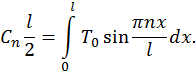

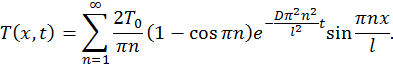
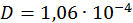 м2/с) толщиной
м2/с) толщиной 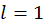 см в различные моменты времени показано на рис. 44. Заметим, что время охлаждения пластины наряду с граничными условиями определяется и параметром
см в различные моменты времени показано на рис. 44. Заметим, что время охлаждения пластины наряду с граничными условиями определяется и параметром 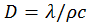 , в чем можно убедиться при самостоятельных расчетах. В частности меньшему значению D соответствует более длительный процесс охлаждения.
, в чем можно убедиться при самостоятельных расчетах. В частности меньшему значению D соответствует более длительный процесс охлаждения.


