ПРИМЕРЫ РЕШЕНИЙ УРАВНЕНИЯ ТЕПЛОПРОВОДНОСТИ
Ниже будут рассмотрены несколько задач на определение температурных полей для относительно простых геометрических и физических условий, которые допускают несложные по форме аналитические решения и вместе с тем дают полезную иллюстрацию характерных физических процессов, связанных с теплопередачей в твердом теле.
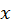 декартовой системы координат, то стационарное уравнение теплопроводности будет иметь вид декартовой системы координат, то стационарное уравнение теплопроводности будет иметь вид
При постоянных значениях коэффициента теплопроводности
Постоянные интегрирования можно найти из граничных условий. Например, если на концах стержня задана температура
Отсюда найдем постоянные интегрирования
Из последней формулы видно, что при отсутствии источников тепловыделения
Рассмотрим теперь другое сочетание граничных условий. Пусть на левом конце стержня внешний источник создает тепловой поток
Выражая эти условия с помощью общего интеграла (75), получим систему относительно постоянных интегрирования
Найдя из полученной системы неизвестные постоянные, получим решение в виде
Как и в предыдущем примере при отсутствии внутренних источников тепловыделения распределение температуры вдоль стержня будет линейным
При этом температура на левом конце стержня, где расположен внешний источник тепла, будет равна В качестве следующего примера найдем стационарное распределение температуры по радиусу в сплошном длинном круговом цилиндре (рис. 39). Существенно упростит задачу в этом случае применение цилиндрической системы координат. В случае цилиндра с большим отношением длины к радиусу и постоянным распределени
 . Тогда стационарное уравнение теплопроводности (71) получит вид . Тогда стационарное уравнение теплопроводности (71) получит вид
Двукратное интегрирование последнего уравнения (при постоянной
Условие симметрии распределения температуры на оси цилиндра (
Откуда имеем
Последнее условие будет выполнено при
Отсюда найдем
В качестве численного примера применения полученного результата рассмотрим распределение температуры в плазме цилиндрического дугового разряда радиусом В следующем примере мы рассмотрим тепловое поле, обладающее сферической симметрией. Такие условия возникают, в частности, если источник тепловыделения малого размера размещен в крупном массиве, например межвитковое дуговое замыкание в обмотке крупной электрической машины. В этом случае совмещая центр сферической системы координат с источником тепловыделения мы можем привести стационарное уравнение теплопроводности (64) к виду:
Дважды интегрируя это уравнение, найдем
 (рис. 40). Примем сопротивление дугового разряда равным (рис. 40). Примем сопротивление дугового разряда равным  Ом, ток разряда Ом, ток разряда  А. Тогда мощность, выделяемая в полости составит А. Тогда мощность, выделяемая в полости составит 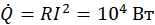 . Рассмотрим решение вне области действия источника тепловыделения . Рассмотрим решение вне области действия источника тепловыделения  . .
Тогда интеграл уравнения теплопроводности упростится
Для вычисления постоянных интегрирования воспользуемся во-первых условием в бесконечно удаленных от места разряда точках
Поскольку
а решение в окончательном виде
При этом температура на границе полости ( Далее рассмотрим более сложные примеры расчета стационарных тепловых полей, имеющие непосредственное отношение к высоковольтной электроэнергетике и технике больших токов. В качестве первого примера этой группы рассмотрим тепловое поле в сечении провода круглого сечения, имеющего канал охлаждения (рис. 41, а). Провода с каналами охлаждения применяют в обмотках мощных электрических машин и катушек для получения сильных магнитных полей. Для данных устройств характерно длительное протекание токов с амплитудой в сотни и даже тысячи Ампер. Например, прокачивается жидкость, например вода, или газ (водород, воздух), что обеспечивает отбор тепловой энергии с внутренней поверхности канала и охлаждение провода в целом. В данном случае мы имеем дело с принудительным конвективным охлаждением поверхности канала, для которой можно использовать обоснованное выше граничное условие третьего рода (67). Если совместить ось
Объемная плотность мощности тепловыделения находится из закона Джоуля-Ленца:
где R — радиус сечения провода, a — радиус охлаждающего канала. Провод снаружи окружен слоями изоляции, обладающей, по сравнению с проводником, относительно низкой теплопроводностью. Поэтому в первом приближении примем внешнюю поверхность провода теплоизолированной, т. е. тепловой поток на ней
На поверхности охлаждающего канала тепловой поток определяется условием третьего рода
где Подставляя в первое из выписанных граничных условий выражение для температуры (76), получим
откуда
откуда находим
Вместе с тем из (76)
Сравнивая последние два выражения, найдем
После подстановки найденных постоянных в общее решение (76) и преобразований получим
Температура на границах сечения провода из полученного решения будет рассчитываться по формулам
Распределение температуры по радиусу сечения для провода с каналом охлаждения с параметрами: Из рис. 41, б следует, что в пределах сечения провода изменение температуры относительно мало по сравнению с ее средней величиной, что объясняется высокой теплопроводностью λ и относительно малыми размерами сечения провода.
Рассчитаем распределение температуры вдоль провода при наличии дефектного контакта. Предыдущий пример показал, что даже в самых жестких условиях изменение температуры в пределах сечения провода весьма мало. Поэтому для нашего расчета можно в первом приближении принять распределение температуры в пределах сечения провода однородным. Распределение тепловыделения вдоль провода зависит от распределения электрического сопротивления вдоль провода, которое однородно вдали от контакта и возрастает при приближении к нему. Совместим ось
где
где S — сечение провода. Охлаждение провода осуществляется естественной конвекцией с его поверхности. Конвективный тепловой поток с единицы длины провода есть
где α — коэффициент теплоотдачи,
Стационарное распределение температуры вдоль провода будет подчиняться уравнению теплопроводности
Для дальнейших преобразований полученного уравнения примем постоянным вдоль провода коэффициент теплопроводности
где
придем к линейному неоднородному дифференциальному уравнению
Решение полученного уравнения будем искать в виде суммы общего решения однородного уравнения
и частного решения в форме правой части
Таким образом, решение будет иметь вид
где четыре постоянных коэффициента
Это условие (при
Далее, подставляя (71) в исходное уравнение (70), получим
Приравнивая коэффициенты при однородных слагаемых в левой и правой части последнего равенства, получим еще два уравнения для определения постоянных интегрирования. При этом с учетом первого условия будем иметь следующую систему для определения констант
решив которую, найдем
Решение уравнения (70), таким образом, будет иметь вид
Выражение в квадратных скобках в (72) при
Откуда найдем температуру на удалении от контакта
Последняя формула удобна для оценки нагрева провода, охлаждаемого в естественных условиях. Погонное электрическое сопротивление есть
Последняя формула ясно указывает на факторы, влияющие на снижение нагрева провода. Это увеличение его поперечного сечения S и электропроводности материала провода, которые ведут к снижению тепловыделения, увеличение периметра сечения
Заметим, что характерные значения показателей экспонент в квадратных скобках
Распределение температуры вдоль провода вблизи контакта для описанного примера при
|

 Рис. 38. Стационарные распределения температуры вдоль стержня
Рис. 38. Стационарные распределения температуры вдоль стержня

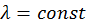 объемной мощности тепловыделения
объемной мощности тепловыделения  последнее уравнение можно дважды проинтегрировать
последнее уравнение можно дважды проинтегрировать (75)
(75)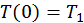 ,
,  . Тогда из (75) имеем
. Тогда из (75) имеем

 и
и 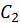 . Решение при указанных граничных условиях получит вид
. Решение при указанных граничных условиях получит вид
 . Температура в стержне меняется по линейному закону от одного граничного значения до другого
. Температура в стержне меняется по линейному закону от одного граничного значения до другого
 . На правом конце стержня сохраним прежнее условие, таким образом, имеем
. На правом конце стержня сохраним прежнее условие, таким образом, имеем
 .
.



 .
. Рис. 39. Распределение температуры по радиусу канала дугового разряда
Рис. 39. Распределение температуры по радиусу канала дугового разряда

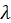 ) дает
) дает
 ) дает
) дает

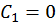 . Пусть на поверхности цилиндра (
. Пусть на поверхности цилиндра ( ) задана температура
) задана температура 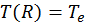 . Тогда можно найти вторую постоянную интегрирования из уравнения
. Тогда можно найти вторую постоянную интегрирования из уравнения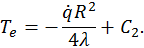

 мм. Граница разрядного канала формируется как область, где прекращаются ионизационные процессы. Выше мы видели, что заметная ионизация газа при нагреве прекращается при
мм. Граница разрядного канала формируется как область, где прекращаются ионизационные процессы. Выше мы видели, что заметная ионизация газа при нагреве прекращается при  K. Поэтому приведенное значение можно принять в качестве граничного
K. Поэтому приведенное значение можно принять в качестве граничного  K. Объемную плотность мощности тепловыделения в плазме разряда найдем из закона Джоуля–Ленца
K. Объемную плотность мощности тепловыделения в плазме разряда найдем из закона Джоуля–Ленца  , где σ — электропроводность плазмы, E — напряженность электрического поля в канале разряда. Характерные для дугового разряда значения составляют
, где σ — электропроводность плазмы, E — напряженность электрического поля в канале разряда. Характерные для дугового разряда значения составляют  1/Ом м,
1/Ом м,  В/м. Теплопроводность дуговой плазмы выше, чем в нейтральном газе, при температурах порядка 10000 К ее значение может принято равным
В/м. Теплопроводность дуговой плазмы выше, чем в нейтральном газе, при температурах порядка 10000 К ее значение может принято равным  . Таким образом, параметр
. Таким образом, параметр  . Распределение температуры по радиусу показано на рис. 39. При этом температура на оси разряда (
. Распределение температуры по радиусу показано на рис. 39. При этом температура на оси разряда (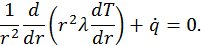

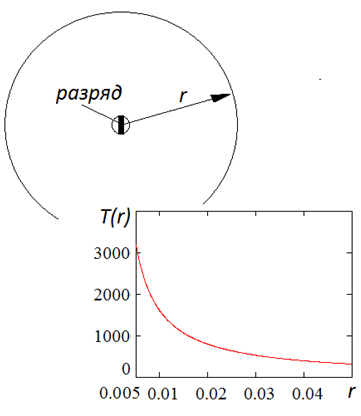 Рис. 40. Распределение температуры вблизи дугового замыкания в сферической полости
Рис. 40. Распределение температуры вблизи дугового замыкания в сферической полости

 , где
, где  C — температура окружающей среды. Из последнего выражения находим
C — температура окружающей среды. Из последнего выражения находим  . Для определения постоянной
. Для определения постоянной 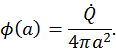
 , то из двух последних уравнений имеем
, то из двух последних уравнений имеем

 мм) при
мм) при  Вт/мК составит
Вт/мК составит  K (рис. 40).
K (рис. 40).
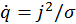 , j — плотность тока, σ — электропроводность,
, j — плотность тока, σ — электропроводность,


 — коэффициент теплоотдачи,
— коэффициент теплоотдачи, 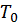 — температура охлаждающего потока. Знак минус в правой части взят вследствие того, что нормаль к внутренней поверхности канала направлена в противоположном к оси
— температура охлаждающего потока. Знак минус в правой части взят вследствие того, что нормаль к внутренней поверхности канала направлена в противоположном к оси  направлении.
направлении.
 . Второе граничное условие дает
. Второе граничное условие дает






 A,
A,  1/Ом м,
1/Ом м,  оС,
оС,  мм,
мм,  см показано на рис. 41, б.
см показано на рис. 41, б. а) б)
Рис. 41. Распределение температуры в сечении провода с каналом охлаждения
а) б)
Рис. 41. Распределение температуры в сечении провода с каналом охлаждения
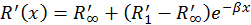 [Ом/м],
[Ом/м], ,
,  — параметр, характеризующий линейный размер контактной области
— параметр, характеризующий линейный размер контактной области  . Мощность тепловыделения на единицу длины провода составляет
. Мощность тепловыделения на единицу длины провода составляет  . В расчете на единицу объема мощность тепловыделения равна
. В расчете на единицу объема мощность тепловыделения равна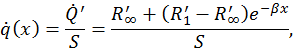



 и
и  , а также в качестве искомой функции вместо T возьмем
, а также в качестве искомой функции вместо T возьмем  :
:
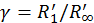 . Далее обозначив
. Далее обозначив и
и  ,
, . (77)
. (77)
 .
. , (78)
, (78) подлежат определению. Поскольку решение должно быть ограниченным при
подлежат определению. Поскольку решение должно быть ограниченным при  , следует положить
, следует положить  . Еще одним условием является симметрия распределения температуры относительно точки контакта
. Еще одним условием является симметрия распределения температуры относительно точки контакта
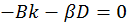 .
.



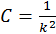 ,
,  ,
,  .
.
 определяет температуру провода вдали от контакта
определяет температуру провода вдали от контакта  :
:

 ,
,  — электропроводность материала провода. Коэффициент теплоотдачи на открытом воздухе
— электропроводность материала провода. Коэффициент теплоотдачи на открытом воздухе  . Температура провода составит
. Температура провода составит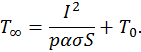
 или, что то же, увеличение развитости поверхности провода, которое ведет к росту теплоотвода с поверхности. Возвращаясь к найденному распределению температуры вдоль провода, можно переписать его в исходных переменных и параметрах
или, что то же, увеличение развитости поверхности провода, которое ведет к росту теплоотвода с поверхности. Возвращаясь к найденному распределению температуры вдоль провода, можно переписать его в исходных переменных и параметрах
 и
и  Вт/м∙ К,
Вт/м∙ К,  1/Ом∙ м) провода диаметром 1 см при
1/Ом∙ м) провода диаметром 1 см при 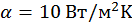 ,
,  м-1. Размер контактного соединения Δ по порядку величины равен диаметру провода. Поэтому
м-1. Размер контактного соединения Δ по порядку величины равен диаметру провода. Поэтому  м-1. Таким образом, вторая экспонента в квадратных скобках последнего выражения очень быстро затухает по сравнению с первой, и выражение для распределения температуры с небольшой потерей точности можно упростить, учтя также, что
м-1. Таким образом, вторая экспонента в квадратных скобках последнего выражения очень быстро затухает по сравнению с первой, и выражение для распределения температуры с небольшой потерей точности можно упростить, учтя также, что 

 Рис. 42. Распределение температуры вдоль провода в области контакта
Рис. 42. Распределение температуры вдоль провода в области контакта
 ,
,  oC, рассчитанное по последней формуле, показано на рис. 42.
oC, рассчитанное по последней формуле, показано на рис. 42.


