Граничные условия для уравнения теплопроводности. Понятие о конвективном теплообмене
Для решения простейших задач теплопроводности мы можем использовать граничные условия первого рода, когда на границе расчетной области S задана температура С помощью условия граничного условия второго рода задается поток энергии на границе расчетной области S: Наряду с указанными условиями, в теории теплопроводности широко применяется граничное условие третьего рода, применяемое на границе раздела твердого тела с жидкостью или газом. Особенностью передачи тепловой энергии от твердой поверхности в газовую или жидкую среду является значительная роль течения, имеющего места вблизи нее. Нагревающийся у поверхности газ отводит от нее энергию не только теплопроводностью, но и переносом нагретых масс газа в области с более низкой температурой. Данный вид теплообмена носит название конвективного. Различают естественную и вынужденную конвекцию. Естественная конвекция. При естественной конвекции поверхность твердого тела отдает часть своей тепловой энергии потоку окружающего газа, который формируется вследствие различия температур в области вблизи твердого тела. Главной гипотезой, на которой основан анализ теплообмена в пристенном слое газа, является условие прилипания. Согласно данному предположению частицы (газа) жидкости, находящиеся в непосредственном контакте со стенкой, адсорбируются последней и теряют скорость — прилипают. Причем слой прилипшего газа можно считать бесконечно тонким. Данная гипотеза нашла подтверждения в совпадении опытных данных с теоретическими результатами, полученными на ее основе. Так как бесконечно тонкий слой газа вблизи поверхности неподвижен, то тепловой поток на границе стенки подчиняется закону Фурье
где n — направление нормали к поверхности.
Если конвективное движение происходит в большом объеме, то на течение газа вблизи некоторой поверхности не влияет свободное движение газа вблизи других объектов. Классическим примером таких условий течения является задача о теплоотдаче на поверхности неограниченной вертикальной пластины при ламинарном режиме течения газа (жидкости) (рис. 36). Распределение вертикальной скорости у поверхности пластины характеризуется нулевыми значениями непосредственно на поверхности вследствие условия прилипания и за пределами пограничного слоя (
где
где толщина пограничного слоя является функцией координаты x (рис. 36)
где
где
Таким образом, тепловой поток с поверхности пластины можно вычислить по формуле
где
Как и в случае естественной конвекции, поток на поверхности обтекаемого тела можно выразить с помощью формулы (74). Коэффициент теплоотдачи для различных условий обтекания можно найти в специальной литературе.
|

 .
. . Поток может создаваться каким-либо внешним источником тепла.
. Поток может создаваться каким-либо внешним источником тепла. , (72)
, (72)

 и вертикальной скорости
и вертикальной скорости  в пограничном слое
в пограничном слое
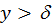 ). Для аппроксимации температуры в пределах пограничного слоя используется аппроксимация
). Для аппроксимации температуры в пределах пограничного слоя используется аппроксимация , (73)
, (73) — толщина пограничного слоя в некоторой точке x по высоте пластины (рис. 36),
— толщина пограничного слоя в некоторой точке x по высоте пластины (рис. 36),  ,
,  — температура газа за пределами пограничного слоя, символом c отмечена точка на поверхности тела. Приближенное интегрирование не приведенных здесь уравнений течения газа вблизи пластины позволяет получить простое выражение для распределения вертикальной скорости в пограничном слое
— температура газа за пределами пограничного слоя, символом c отмечена точка на поверхности тела. Приближенное интегрирование не приведенных здесь уравнений течения газа вблизи пластины позволяет получить простое выражение для распределения вертикальной скорости в пограничном слое ,
, ,
, — ускорение силы тяжести,
— ускорение силы тяжести,  — коэффициент вязкости газа (жидкости),
— коэффициент вязкости газа (жидкости),  — коэффициент теплового расширения газа. Вычисляя тепловой поток на границе тела в соответствии с (72) и дифференцируя (73) с учетом выражения для толщины пограничного слоя d, нетрудно получить
— коэффициент теплового расширения газа. Вычисляя тепловой поток на границе тела в соответствии с (72) и дифференцируя (73) с учетом выражения для толщины пограничного слоя d, нетрудно получить ,
, .
. , (74)
, (74) — температура за пределами пограничного слоя. Коэффициент
— температура за пределами пограничного слоя. Коэффициент  называется коэффициентом теплоотдачи. Выражение (74) представляет собой граничное условие третьего рода и дает значение теплового потока на твердой поверхности. В частности при свободной конвекции с ребристой поверхности изоляционных конструкций
называется коэффициентом теплоотдачи. Выражение (74) представляет собой граничное условие третьего рода и дает значение теплового потока на твердой поверхности. В частности при свободной конвекции с ребристой поверхности изоляционных конструкций  .
. Рис. 37. Распределение скорости потока
Рис. 37. Распределение скорости потока  и температуры T в пограничном слое толщиной
и температуры T в пограничном слое толщиной  при вынужденной конвекции
при вынужденной конвекции



